Lời giải

+) Ta biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}y-2x\le 2\\ y\le 4\\ x\le 5\\ x+y\ge -1\end{array}\right.$

+ Xác định miền nghiệm của bất phương trình y – 2x ≤ 2.

- Vẽ đường thẳng y – 2x = 2

- Ta có: 0 – 2.0 = 0 < 2.

Do đó, miền nghiệm của bất phương trình  y – 2x ≤ 2 là nửa mặt phẳng có bờ là đường thẳng y – 2x = 2 (tính cả đường thẳng đó) và chứa điểm O(0; 0).

+ Xác định miền nghiệm của bất phương trình y ≤ 4.

- Vẽ đường thẳng y = 4.

- Ta có 3 ≤ 4

Do đó, miền nghiệm của bất phương trình y ≤ 4 là nửa mặt phẳng có bờ là đường thẳng y = 4 (tính cả đường thẳng đó) và chứa điểm (0; 3).

+ Xác định miền nghiệm của bất phương trình x ≤ 5.

- Vẽ đường thẳng x = 5.

- Ta có 3 ≤ 5

Do đó, miền nghiệm của bất phương trình x ≤ 5 là nửa mặt phẳng có bờ là đường thẳng x = 5 (tính cả đường thẳng đó) và chứa điểm (3; 0).

+ Xác định miền nghiệm của bất phương trình x + y ≤ – 1.

- Vẽ đường thẳng x + y = -1

- Ta có: 0 + 0 = 0 > -1.

Do đó, miền nghiệm của bất phương trình  x + y ≥ -1 là nửa mặt phẳng có bờ là đường thẳng x + y = -1 (tính cả đường thẳng đó) và không chứa điểm O(0; 0).

Vậy miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCD (miền tô màu vàng) với tọa độ các đỉnh A(1; 4); B(5; 4); C(5; – 6); D(– 1; 0)

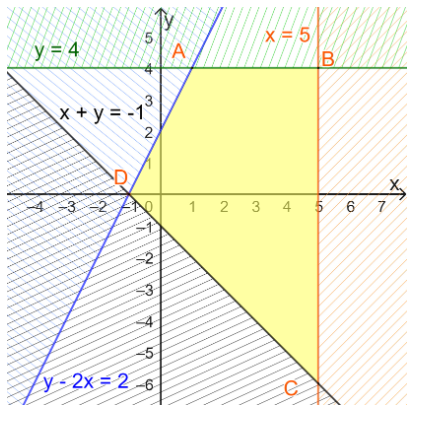
Giá trị lớn nhất và giá trị nhỏ nhất của F(x; y) = – x – y được xác định với (x; y) là tọa độ của một trong bốn đỉnh A; B; C; D.

F(1; 4) = – 1 – 4 = – 5

F(5; 4) = – 5 – 4 = – 9

F(5; – 6) = – 5 – (– 6) = 1

F(– 1; 0) = – (– 1) – 0 = 1

Vậy giá trị lớn nhất của biểu thức F là 1 tại (x;y) = (-1;0) hoặc (x;y) = (5;-6) và giá trị nhỏ nhất của biểu thức F là -9 tại (x;y) = (5;4)​