Lời giải

Gọi số tiền bác An đầu tư cho trái phiếu chính phủ, trái phiếu ngân hàng lần lượt là x, y (triệu đồng) (0 ≤ x, y ≤ 1 200).

Khi đó bác An đầu tư cho trái phiếu doanh nghiệp là 1 200 – x – y (triệu đồng)

Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có: x ≥ 3y hay x – 3y ≥ 0.

Để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên ta có: 1 200 – x – y ≤ 200 hay x + y ≥ 1 000.

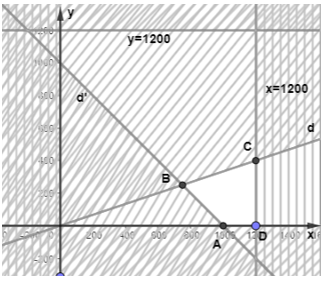
Từ đó ta có hệ bất phương trình: $\left\{\begin{array}{l}0\le x\le 1200\\ 0\le y\le 1200\\ x-3y\ge 0\\ x+y\ge 1000\end{array}\right.$.

Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với tọa độ các điểm

A(1 000;0), B(750;250), C(1 200;400), D(1 200;0).

Lợi nhuận bác An thu được là: F(x;y) = 7%x + 8%y + 12%(1200 – x – y) =  144 – 0,05x – 0,04y (triệu đồng)

Tính giá trị của F(x;y) tại các điểm A, B, C, D, ta được:

F(1 000;0) = 144 – 0,05.1 000 – 0,04.0 = 94;

F(750;250) = 144 – 0,05.750 – 0,04.250 = 96,5;

F(1 200;400) = 144 – 0,05.1 200 – 0,04.400 = 68;

F(1 200;0) = 144 – 0,05.1 200 – 0,04.0 = 84;

Suy ra F(x; y) lớn nhất bằng 96,5 khi x = 750, y = 250.

Vậy bác An nên đầu tư 750 triệu đồng vào trái phiếu chính phủ, 250 triệu đồng vào trái phiếu ngân hàng và 200 triệu đồng vào trái phiếu doanh nghiệp để lợi nhuận thu được là lớn nhất.