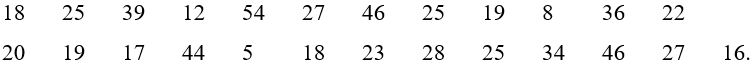Câu hỏi:
128 lượt xemBài 3.3 trang 61 Toán 11 Tập 1: Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:
Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.
Lời giải
Hướng dẫn giải:
Giá trị nhỏ nhất của mẫu số liệu là 492, giá trị lớn nhất của mẫu số liệu là 653, do đó khoảng biến thiên của mẫu số liệu là R = 653 – 492 = 161. Ta cần chia thành bảy nhóm có độ dài bằng nhau. Để cho thuận tiện, ta chọn đầu mút trái của nhóm đầu tiên là 485 và đầu mút phải của nhóm cuối cùng bằng 660 và độ dài của mỗi nhóm bằng 25 ta được các nhóm là [485; 510), [510; 535), [535; 560), [560; 585), [585; 610), [610; 635), [635; 660]. Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
|
Thời gian |
[485; 510) |
[510; 535) |
[535; 560) |
[560; 585) |
[585; 610) |
[610; 635) |
[635; 660] |
|
Số cầu thủ |
8 |
2 |
1 |
2 |
1 |
1 |
1 |