Câu hỏi:
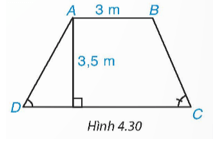
110 lượt xemMặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Lời giải
Hướng dẫn giải:
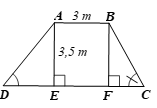
Kẻ AE ⊥ CD, BF ⊥ CD. Khi đó AE // BF.
Vì ABCD là hình thang nên AB // CD, do đó suy ra AB // EF.
Xét tứ giác ABFE có: AE // BF và AB // EF nên là hình bình hành.
Lại có nên hình bình hành ABFE là hình chữ nhật.
Suy ra EF = AB = 3 m.
Xét ∆ADE vuông tại E, ta có:
suy ra
Vì ABFE là hình chữ nhật nên BF = AE = 3,5 m.
Xét ∆BCF vuông tại F, ta có:
suy ra
Ta có:
Xét ∆ADE vuông tại E, theo định lí Pythagore, ta có:
AD2 = AE2 + DE2 = 3,52 + 2,82 = 20,09.
Suy ra
Xét ∆BCF vuông tại F, theo định lí Pythagore, ta có:
Suy ra