Câu hỏi:
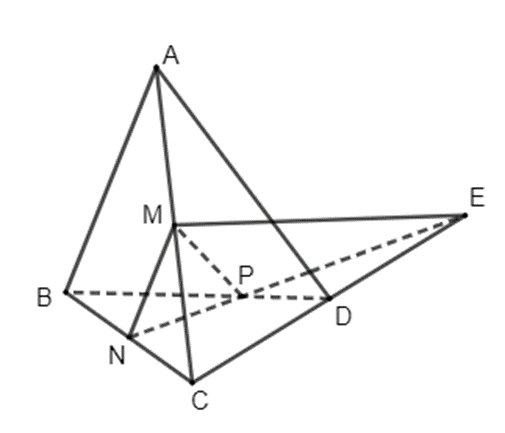
124 lượt xemBài 4.6 trang 77 Toán 11 Tập 1: Cho hình tứ diện ABCD. Trên các cạnh AC, BC, BD lần lượt lấy các điểm M, N, P sao cho AM = CM, BN = CN, BP = 2DP.
a) Xác định giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Xác định giao tuyến của hai mặt phẳng (ACD) và (MNP).
Lời giải
Hướng dẫn giải:
a) Trong tam giác BCD, N thuộc cạnh BC thỏa mãn BN = CN hay N là trung điểm của BC và P thuộc cạnh BD sao cho BP = 2DP. Khi đó, đường thẳng NP cắt CD tại một điểm E. Vì E thuộc NP nằm trong mặt phẳng (MNP) nên E thuộc mặt phẳng (MNP). Vậy E là giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Vì M thuộc cạnh AC nên M thuộc mặt phẳng (ACD), vì E thuộc CD nên E thuộc mặt phẳng (ACD), do đó đường thẳng ME nằm trong mặt phẳng (ACD).
Vì E thuộc mặt phẳng (MNP) và M thuộc mặt phẳng (MNP) nên ME nằm trong mặt phẳng (MNP).
Vậy ME là giao tuyến của hai mặt phẳng (ACD) và (MNP).
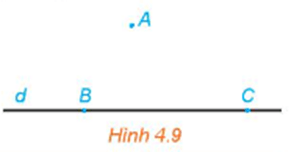
Câu hỏi trang 72 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?