Lời giải

Cổng Trường Đại học Bách khoa Hà Nội có dạng là một parabol, gọi dạng parabol này là y = ax2 + bx + c với a ≠ 0.

Chọn hệ trục tọa độ Oxy như hình vẽ với Oy là trục đối xứng của cổng:

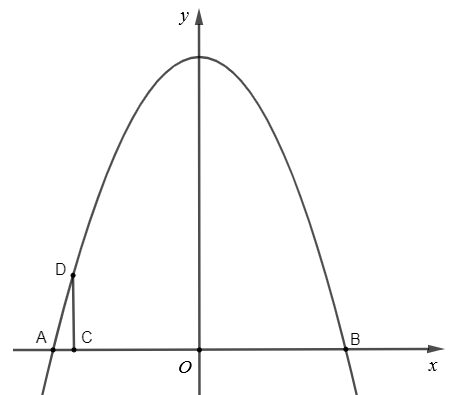
Khoảng cách giữa hai chân cổng AB = 8 m.

Vì Oy là trục đối xứng của parabol nên O là trung điểm của AB, do đó AO = OB = 4 m.

Lấy điểm C cách A một khoảng 0,5 m, theo bài ra, chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5 m là 2,93 m nên CD = 2,93 m.

CO = AO – AC = 4 – 0,5 = 3,5 m.

Vậy ta xác định được tọa độ các điểm: A(– 4; 0), B(4; 0), C(– 3,5; 0), D(– 3,5; 2,93).

Parabol đi qua các điểm A, B, D nên phương trình y = ax2 + bx + c thỏa mãn tọa độ các điểm A, B, D, thay tọa độ các điểm tương ứng ta có:

0 = a . (– 4)2 + b . (– 4) + c ⇔ 16a – 4b + c = 0 (1)

0 = a . 42 + b . 4 + c ⇔ 16a + 4b + c = 0 (2)

2,93 = a . (– 3,5)2 + b . (– 3,5) + c = 0 ⇔ 12,25a – 3,5b + c = 2,93 (3)

Lấy (2) trừ (1) theo vế ta được 8b = 0 ⇔ b = 0 thay vào (1) và (3) ta có hệ:

$\left\{\begin{array}{l}16a+c=0\\ \mathrm{12,25}a+c=\mathrm{2,93}\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{-293}{375}\\ c=\frac{4688}{375}\end{array}\right.$

Vậy parabol $y=\frac{-293}{375}{x}^2+\frac{4688}{375}$ có tọa độ đỉnh I$\left(0;\frac{4688}{375}\right)$.

Chiều cao của cổng parabol là tung độ đỉnh I và bằng $\frac{4688}{375}\approx \mathrm{12,5}$m.

Vậy kết quả của bạn An tính ra là không chính xác.