Câu hỏi:
145 lượt xem2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
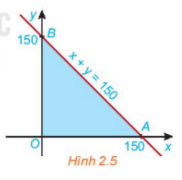
HĐ 2 trang 27 Toán 10 Tập 1: Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định các miền nghiệm D1, D2, D3 của các bất phương trình tương ứng x ≥ 0, y ≥ 0 và x + y ≤ 150.
b) Miền tam giác OAB (H.2.5) có phải là giao của các miền nghiệm D1, D2, D3 hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
Lời giải
Hướng dẫn giải:
Lời giải
a)
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0), tính cả Oy.
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1), tính cả Ox.
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 150.
- Vẽ đường thẳng d: x + y – 150 = 0.
- Vì 0 + 0 = 0 < 150 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 150
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ, kể cả đường thẳng d.
b) Giao điểm của ba miền nghiệm D1, D2, D3 là miền tam giác OAB với O(0;0), A(150;0) và B(0;150)
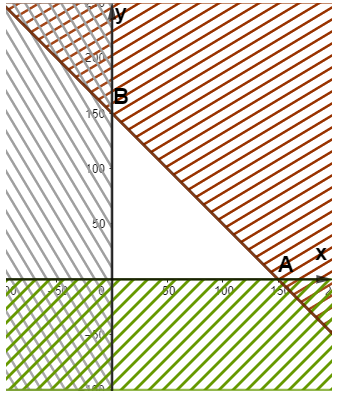
Do đó miền tam giác OAB (H.2.5) có là giao của các miền nghiệm D1, D2, D3.
c) Điểm (1; 2) nằm trong tam giác OAB thỏa mãn x = 1 > 0, y = 2 > 0 và 1 + 2 = 3 < 150 nên cặp số (x; y) = (1;2) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.
Điểm (1;149) nằm trong tam giác OAB thỏa mãn x = 1 > 0, y = 149 > 0 và 1 + 149 = 150 ≤ 150 nên cặp số (x; y) = (1;149) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.