Câu hỏi:
124 lượt xem Tự luận
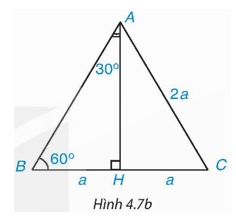
Xét tam giác đều ABC có cạnh bằng 2a.
a) Tính đường cao AH của tam giác ABC (H.4.7b).
b) Tính sin30°, cos30°, sin60° và cos60°.
c) Tính tan30°, cot30°, tan60° và cot60°.
Lời giải
Hướng dẫn giải:
a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó H là trung điểm của BC nên
Xét ∆ABH vuông tại H, theo định lí Pythagore, ta có:
AB2 = AH2 + HB2, suy ra AH2 = AB2 – HB2 = (2a)2 – a2 = 4a2 – a2 = 3a2.
Do đó
b) Tam giác ABC đều nên
Tam giác ABC đều có đường cao AH nên AH cũng là đường phân giác của của tam giác. Do đó
Do đó
c)
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 15:
Câu 16:
Câu 17:
Câu 18:
Câu 19:
Câu 20: