Câu hỏi:
124 lượt xemGiải Toán 10 trang 9 Tập 2
Luyện tập 3 trang 9 Toán 10 Tập 2: Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x2. Hãy cho biết:
a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên ℝ.
b) Hàm số y = – 2x2 đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).
Lời giải
Hướng dẫn giải:
Lời giải
Vẽ các đồ thị hàm số:
* Hàm số y = 3x + 1
Tập xác định của hàm số là ℝ.
Với x = 0 thì y = 3 . 0 + 1 = 1
Với x = – 1 thì y = 3 . (– 1) + 1 = – 2
Vậy đồ thị hàm số y = 3x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; – 2).
* Hàm số y = – 2x2
Tập xác định của hàm số là ℝ.
Bảng giá trị tương ứng của x và y
|
x |
0 |
1 |
– 1 |
2 |
– 2 |
|
y = – 2x2 |
0 |
– 2 |
– 2 |
– 8 |
– 8 |
Trên mặt phẳng tọa độ, lấy năm điểm có tọa độ là (0; 0), (1; – 2), (– 1; – 2), (2; – 8), (– 2; – 8) rồi vẽ đường cong đi qua năm điểm trên ta được đồ thị của hàm số y = – 2x2.
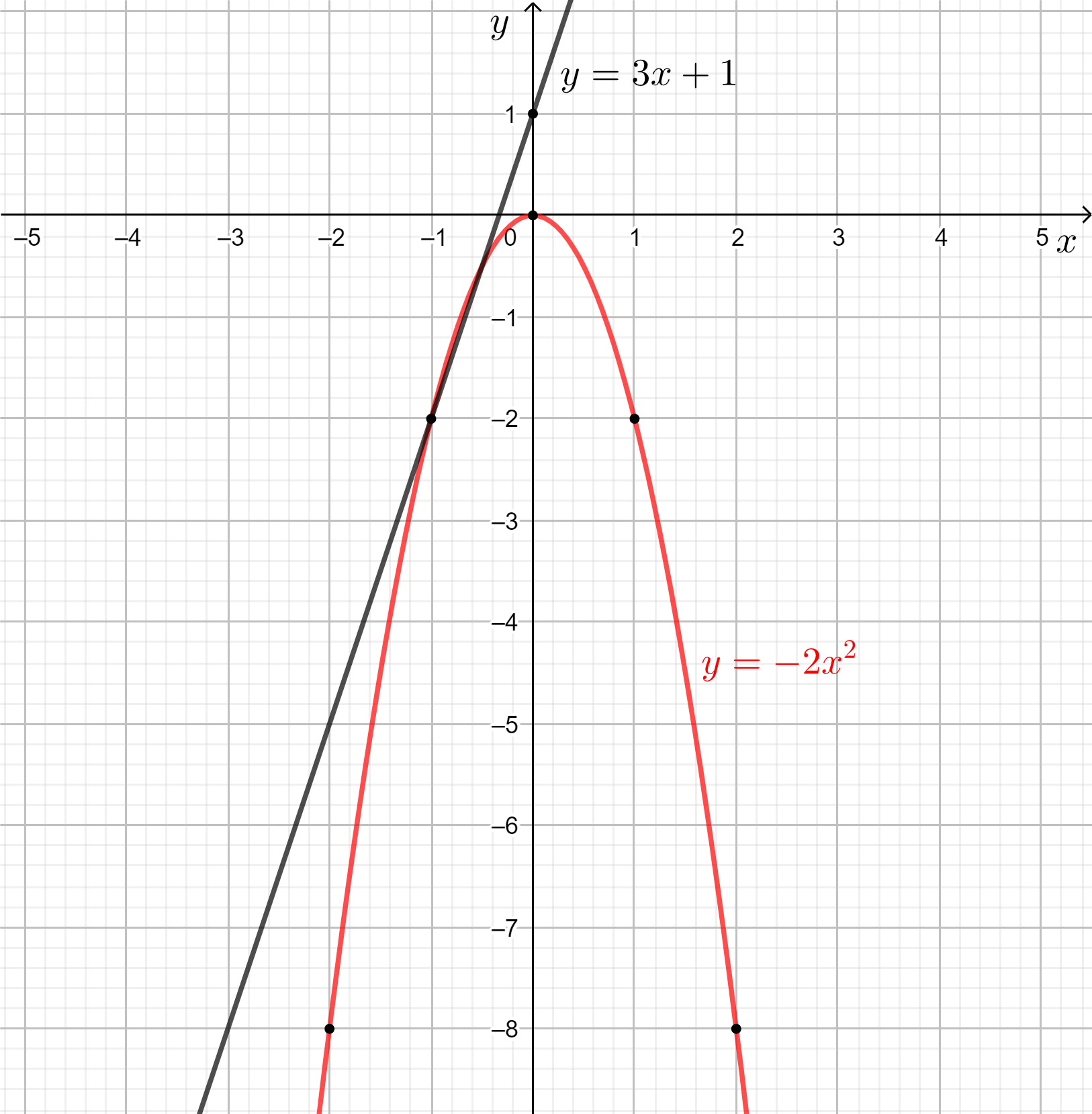
a) Từ hình trên trên, ta thấy đồ thị hàm số y = 3x + 1 đi lên từ trái sang phải trên ℝ nên hàm số y = 3x + 1 đồng biến trên ℝ.
b) Từ hình trên, ta có:
- Trên khoảng (– ∞; 0), đồ thị hàm số y = – 2x2 đi lên từ trái sang phải nên hàm số đồng biến trên khoảng này.
- Trên khoảng (0; + ∞), đồ thị hàm số y = – 2x2 đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng này.