Câu hỏi:
125 lượt xemGiải bài tập Toán 10 Bài 16: Hàm số bậc hai
A. Các câu hỏi trong bài
Giải Toán 10 trang 11 Tập 2
Mở đầu trang 11 Toán 10 Tập 2: Bác Việt có một tấm lưới hình chữ nhật dài 20 m. Bác muốn dùng tấm lưới này rào chắn ba mặt áp bên bờ tường của khu vườn nhà mình thành một mảnh đất hình chữ nhật để trồng rau.
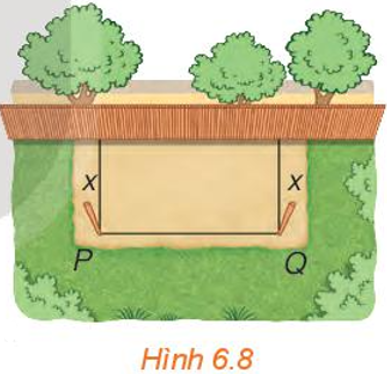
Hỏi hai cột góc hàng rào cần phải cắm cách bờ tường bao xa để mảnh đất được rào chắn của bác có diện tích lớn nhất?
Lời giải
Hướng dẫn giải:
Lời giải
Sau bài học này, ta giải quyết được bài toán trên như sau:
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc P và Q đến bờ tường.
Tấm lưới dài 20 m và được rào chắn ba mặt như Hình 6.8, nên x + x + PQ = 20.
Do đó, PQ = 20 – x – x = 20 – 2x (m).
Vì PQ > 0 nên 20 – 2x > 0 ⇔ 2x < 20 ⇔ x < 10.
Vậy điều kiện của x là 0 < x < 10.
Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là x (m) và 20 – 2x (m) với 0 < x < 10.
Vậy diện tích của mảnh đất là S(x) = x . (20 – 2x) = – 2x2 + 20x.
Theo yêu cầu bài toán, ta cần tìm giá trị của x để S(x) lớn nhất.
S(x) = – 2(x2 – 10x) = – 2(x2 – 2 . 5 . x + 25) + 50 = – 2(x – 5)2+ 50 ≤ 50.
Dấu “=” xảy ra khi x – 5 = 0 ⇔ x = 5 (thỏa mãn điều kiện 0 < x < 10).
Khi đó, giá trị lớn nhất của S(x) là 50 tại x = 5.
Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5 m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất.