(2023) Đề thi thử Toán THPT Chuyên Vĩnh Phúc có đáp án

Câu 1:

Cho hình nón có bán kính đáy

r = \sqrt{3}

và độ dài đường sinh l = 4. Tính diện tích xung quanh của hình nón đã cho.

A. $S_{x q} = 12 π \cdot$

B. $S_{x q} = 8 \sqrt{3} π \cdot$

C. $S_{x q} = 4 \sqrt{3} π \cdot$

D. $S_{x q} = \sqrt{39} π \cdot$

Câu 2:

Một vật chuyển động theo quy luật

s = \frac{1}{3} t^{3} - t^{2} + 9 t

với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

A. $89 (m / s) \cdot$

B. $71 (m / s) \cdot$

C. $109 (m / s) \cdot$

D. $\frac{25}{3} (m / s) \cdot$

Câu 3:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a Gọi M là trung điểm của CD. Tính khoảng cách từ M đến (SAB)

A. $a \sqrt{2} \cdot$

B. $\frac{a \sqrt{2}}{2} \cdot$

C. a

D. 2a

Câu 4:

Cho a là số thực dương khác 1. Giá trị của biểu thức

\log_{a} (\frac{a^{2} \sqrt[3]{a^{2}} \sqrt[5]{a^{4}}}{\sqrt[15]{a^{7}}})

bằng

A. 3

B. $\frac{9}{5} \cdot$

C. $\frac{12}{5} \cdot$

D. 2

Câu 5:

Biết phương trình

\log_{9}^{2} x + \log_{3} \frac{x}{27} = 0

có hai nghiệm

x_{1}, x_{2}

với

x_{1} < x_{2}

. Hiệu

x_{2} - x_{1}

bằng

A. $\frac{80}{3}$

B. $\frac{6560}{729}$

C. $\frac{80}{27}$

D. $\frac{6560}{27}$

Câu 6:

Với a là số thực thoả mãn

0 < a \neq 1

, giá trị biểu thức

a^{3 \log_{a} 2}

bằng

A. 2

B. 3

C. 6

D. 8

Câu 7:

Hàm số

y = x^{4} - 2

nghịch biến trên khoảng nào?

A. $(\frac{1}{2}; + \infty)$

B. $(- \infty; \frac{1}{2})$

C. $(0; + \infty)$

D. $(- \infty; 0)$

Câu 8:

Phương trình

\log_{2} (x + 1) = 4

có nghiệm là

A. x = 15

B. x = 16

C. x = 3

D. x = 4

Câu 9:

Hàm số

y = \frac{1}{3} x^{3} + x^{2} - 3 x + 1

đạt cực tiểu tại điểm

A. x = -1

B. x = 3

C. x = 1

D. x = -3

Câu 10:

Hàm số nào sau đây có đồ thị như hình bên?

A. $y = - \frac{x^{3}}{3} + x^{2} + 1$

B. $y = x^{3} - 3 x^{2} + 1$

C. $y = x^{3} - 3 x^{2} - 1$

D. $y = - x^{3} - 3 x^{2} + 1$

Câu 11:

Trong các hàm số sau, hàm số nào đồng biến trên R?

A. $y = \frac{x - 2}{x + 1}$

B. $y = 3 x^{3} + 3 x - 2$

C. $y = x^{4} + 3 x^{2}$

D. $y = 2 x^{3} - 5 x + 1$

Câu 12:

Cho hình chóp tứ giác đều có cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi a là góc giữa mặt bên và mặt đáy. Mệnh đề nào dưới đây là đúng?

A. $cos α = \frac{\sqrt{14}}{14}$

B. $cos α = \frac{\sqrt{2}}{4}$

C. $cos α = \frac{\sqrt{2}}{2}$

D. $cos α = \frac{\sqrt{10}}{10}$

Câu 13:

Cho khối chóp S.ABCD có thể tích V = 32. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Thể tích khối đa diện MNPQABCD bằng

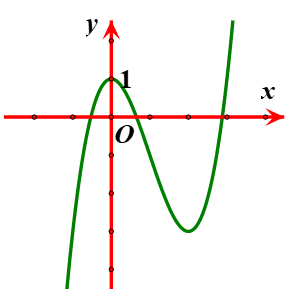
A. 28

B. 16

C. 2

D. 4

Câu 14:

Tính thể tích V của khối chóp có diện tích đáy bằng B và chiều cao bằng h là

A. $V = B h \cdot$

B. $V = \frac{1}{6} B h \cdot$

C. $V = \frac{1}{2} B h \cdot$

D. $V = \frac{1}{3} B h \cdot$

Câu 15:

Cho khối lăng trụ tam giác ABC.A'B'C', biết rằng thể tích khối chóp A'.AB'C bằng 9 (đvdt). Tính thể tích khối lăng trụ đã cho

A. $V = 1 (đ v d t) .$

B. $V = 27 (đ v d t) .$

C. $V = \frac{3}{2} (đ v d t) .$

D. $V = \frac{3}{4} (đ v d t) .$

Câu 16:

Hàm số

f (x) = \log_{2} (x^{2} - 2)

có đạo hàm là

A. $f^{'} (x) = \frac{1}{(x^{2} - 2) \ln 2} \cdot$

B. $f^{'} (x) = \frac{\ln 2}{(x^{2} - 2)} \cdot$

C. $f^{'} (x) = \frac{2 x \ln 2}{(x^{2} - 3)} \cdot$

D. $f^{'} (x) = \frac{2 x}{(x^{2} - 2) \ln 2} \cdot$

Câu 17:

Một phòng có 12 người. Cần lập một tổ đi công tác gồm 3 người, một người là tổ trưởng, một người làm tổ phó và một người làm thành viên. Hỏi có bao nhiêu cách lập?

A. 1320

B. 1230

C. 220

D. 1728

Câu 18:

Cho đa giác đều P gồm 16 đỉnh. Chọn ngẫu nhiên một tam giác có ba đỉnh là đỉnh của P. Tính xác suất để tam giác chọn được là tam giác vuông.

A. $\frac{3}{14}$

B. $\frac{1}{5}$

C. $\frac{2}{3}$

D. $\frac{6}{7}$

Câu 19:

Biết rằng đồ thị hàm số

y = x^{4} - 2 a x^{2} + b

có một điểm cực trị (1;2). Tính khoảng cách giữa điểm cực đại và điểm cực tiểu của độ thị đã cho.

A. $\sqrt{5}$

B. $\sqrt{2}$

C. 2

D. $\sqrt{26}$

Câu 20:

Đạo hàm của hàm số

y = 4^{x^{2} + x + 1}

A. $y' = (2 x + 1) 4^{x^{2} + x + 1} . \ln 2$

B. $y' = (2 x + 1) 4^{x^{2} + x + 1} . \ln 4$

C. $y' = \frac{(2 x + 1) 4^{x^{2} + x + 1}}{\ln 4}$

D. $y' = 4^{x^{2} + x + 1} . \ln 2$

Câu 21:

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số

y = \frac{2 x + 1}{x + 5}

?

A. x = -1

B. x = 1

C. y = 2

D. y = -1

Câu 22:

Cho hình nón có chiều cao và bán kính đáy đều bằng 1. Mặt phẳng (P) qua đỉnh của hình nón và cắt đáy theo dây cung có độ dài bằng 1. Khoảng cách từ tâm của đáy tới mặt phẳng (P) bằng

A. $\frac{\sqrt{3}}{3} .$

B. $\frac{\sqrt{7}}{7} .$

C. $\frac{\sqrt{21}}{7} .$

D. $\frac{\sqrt{2}}{2} .$

Câu 23:

Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4%/ tháng. Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền ( cả vốn ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi?

A. $102423000$ (đồng)

B. $102160000$ (đồng)

C. $102017000$ (đồng)

D. $102424000$ (đồng)

Câu 24:

Đường tiệm cận đứng của đồ thị hàm số $y = \frac{3 x + 2022}{x - 1}$ có phương trình là

A. x = 1

B. x = 3

C. y = 3

D. y = 1

Câu 25:

Trên đoạn [-2;1], hàm số

y = x^{3} + 3 x^{2} - 1

đạt giá trị nhỏ nhất tại điểm

A. x = -2

B. x = -1

C. x = 0

D. x = 1

Câu 26:

Cho hàm số y = f(x) có đạo hàm $f^{'} (x) = (x - 1) (x^{2} - 3 x + 3), \forall x \in ℝ$ . Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(- \infty; - 1)$

B. (1;3)

C. (-1;3)

D. $(1; + \infty)$

Câu 27:

Cho $α, β$ là các số thực. Đồ thị các hàm số $y = x^{α}, y = x^{β}$ trên khoảng $(0; + \infty)$ được cho trong hình vẽ bên.

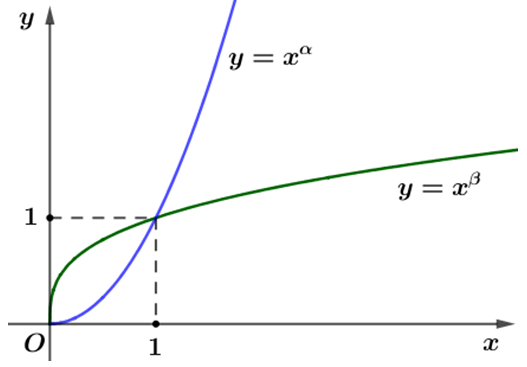
Cho anpha, beta là các số thực. Đồ thị các hàm số y = x^anpha, y = x ^ beta trên khoảng 0 đến dương vô cùng được cho trong hình vẽ bên. (ảnh 1)

A. $β < 0 < 1 < α$

B. $α < 0 < 1 < β$

C. $0 < β < 1 < α$

D. $0 < α < β < 1$

Câu 28:

Hình tứ diện đều có tất cả bao nhiêu mặt phẳng đối xứng?

A. 2

B. 4

C. 3

D. 6

Câu 29:

Thể tích khối hộp chữ nhật có ba kích thước bằng

a, a \sqrt{2}, a \sqrt{3}

là

A. $\frac{a^{3} \sqrt{6}}{3} \cdot$

B. $\frac{a^{3} \sqrt{6}}{2} \cdot$

C. $\frac{a^{3} \sqrt{6}}{6} \cdot$

D. $a^{3} \sqrt{6} \cdot$

Câu 30:

Tính thể tích Vcủa khối lăng trụ tam giác đều có tất cả các cạnh bằng cạnh a

A. $V = \frac{a^{3} \sqrt{3}}{12} \cdot$

B. $V = \frac{a^{3} \sqrt{3}}{2} \cdot$

C. $V = \frac{a^{3} \sqrt{3}}{4} \cdot$

D. $V = \frac{a^{3} \sqrt{3}}{6} \cdot$

Câu 31:

Cho a, b là các số thực thoã mãn

{(\sqrt{2} - 1)}^{a} > {(\sqrt{2} - 1)}^{b}

. Kết luận nào sau đây đúng?

A. a > b

B. a = b

C. a < b

D. $a \geq b \cdot$

Câu 32:

Cho hàm số bậc ba y = f(x) có đồ thị đạo hàm y = f'(x) như hình sau:

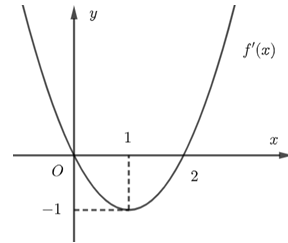
Hàm số đã cho nghịch biến trên khoảng nào?

A. (1;2)

B. (3;4)

C. (2;3)

D. (-1;0)

Câu 33:

Tìm tập xác định D của hàm số

y = {(x^{2} - 3 x)}^{- 4}

A. $D = ℝ \ \{0; 3\}$

B. $D = (- \infty; 0) \cup (3; + \infty)$

C. D = R

D. (0;3)

Câu 34:

Tổng các nghiệm của phương trình

3^{x^{2} - 3 x} = \frac{1}{9}

bằng

A. 3

B. 4

C. 2

D. -2

Câu 35:

Có bao nhiêu giao điểm của đồ thị hàm số $y = x^{3} + 3 x - 3$ với trục Ox

A. 2

B. 1

C. 3

D. 0

Câu 36:

Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên dưới. Hỏi hàm số

g (x) = f (x^{2} - 5)

có bao nhiêu khoảng nghịch biến?

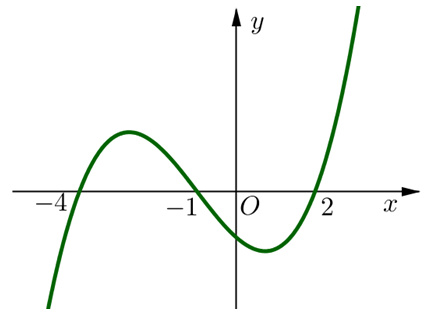
A. 3

B. 2

C. 5

D. 4

Câu 37:

Cho hàm số y = f(x) có bảng biến thiên như sau

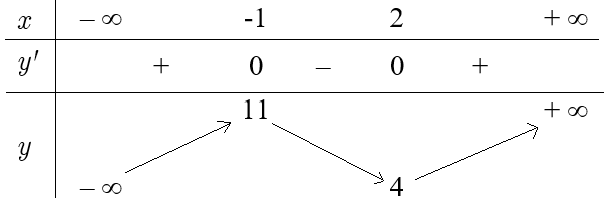
Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số g(x) = trị tuyệt đối f(x) - 3m có 5 điểm cực trị? (ảnh 1)

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $g (x) = |f (x) - 3 m|$ có 5 điểm cực trị?

A. 1

B. 4

C. 3

D. 2

Câu 38:

Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác vuông tại A, AB = 2 ; $A C = \sqrt{3}$ . Góc $\hat{C A A'} = 90^{0}$ , $\hat{B A A'} = 120^{0}$ . Gọi M là trung điểm cạnh BB'. Biết CM vuông góc với A'B, tính thể tích khối lăng trụ đã cho.

A. $V = \frac{1 + \sqrt{33}}{8} .$

B. $V = \frac{1 + \sqrt{33}}{4} .$

C. $V = \frac{3 (1 + \sqrt{33})}{4} .$

D. $V = \frac{3 (1 + \sqrt{33})}{8} .$

Câu 39:

Cho khối chóp S.ABC có

\hat{A S B} = \hat{B S C} = \hat{C S A} = 60 °

, SA = a, SB = 2a, SC = 4a. Tính thể tích khối chóp S.ABC theo a

A. $\frac{2 a^{3} \sqrt{2}}{3}$

B. $\frac{8 a^{3} \sqrt{2}}{3}$

C. $\frac{4 a^{3} \sqrt{2}}{3}$

D. $\frac{a^{3} \sqrt{2}}{3}$

Câu 40:

Giả sử phương trình $25^{x} + 15^{x} = {6.9}^{x}$ có một nghiệm duy nhất được viết dưới dạng $\frac{a}{\log_{b} c - \log_{b} d}$ với a là số nguyên dương và b, c, d là các số nguyên tố. Tính $S = a^{2} + b + c + d$ .

A. S = 14

B. S = 11

C. S = 19

D. S = 12

Câu 41:

Tìm số giá trị nguyên thuộc đoạn [-2022;2022] của tham số m để đồ thị hàm số

y = \frac{\sqrt{x - 3}}{x^{2} + x - m}

có đúng hai đường tiệm cận.

A. 2010

B. 2008

C. 2009

D. 2011

Câu 42:

Có tất cả bao nhiêu bộ ba số thực (x; y; z) thoả mãn đồng thời các điều kiện dưới đây $2^{\sqrt[3]{x^{2}}} {.4}^{\sqrt[3]{y^{2}}} {.16}^{\sqrt[3]{z^{2}}} = 128$ và ${(x y^{2} + z^{4})}^{2} = 4 + {(x y^{2} - z^{4})}^{2}$

A. 4

B. 2

C. 1

D. 3

Câu 43:

Cho hình chóp tứ giác có độ dài cạnh đáy bằng a và chiều cao bằng 2a. Tính theo a thể tích của khối đa diện có các đỉnh là trung điểm các cạnh của hình chóp đã cho

A. $\frac{a^{3}}{12}$

B. $\frac{5 a^{3}}{12}$

C. $\frac{5 a^{3}}{24}$

D. $\frac{3 a^{3}}{8}$

Câu 44:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với

A B = a, A D = 2 a, S A ⊥ (A B C D)

và SA = a. Gọi N là trung điểm của CD. Tính khoảng cách từ A đến mặt phẳng (SBN)

A. $\frac{a \sqrt{33}}{33}$

B. $\frac{4 a \sqrt{33}}{33}$

C. $\frac{a \sqrt{33}}{11}$

D. $\frac{2 a \sqrt{33}}{33}$

Câu 45:

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ)$ có đồ thị như hình vẽ

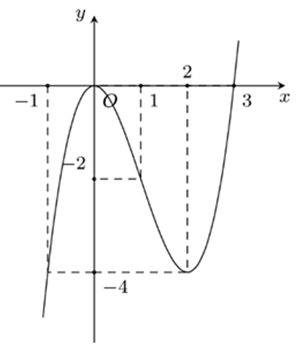
Cho hàm số y = f(x) = ax^3 + bx^2 + cx + d (a, b, c, d thuộc R) có đồ thị như hình vẽ Tổng tất cả các giá trị nguyên của tham số m để phương trình (ảnh 1)

Tổng tất cả các giá trị nguyên của tham số m để phương trình $f^{2} (x) - (m + 5) |f (x)| + 4 m + 4 = 0$ có 7 nghiệm phân biệt là

A. 3

B. 6

C. -6

D. 4

Câu 46:

Khối tròn xoay sinh bởi một tam giác đều cạnh a (kể cả điểm trong) khi quay quanh một đường thẳng chứa một cạnh của tam giác có thể tích bằng

A. $\frac{π a^{3}}{4} .$

B. $\frac{π a^{3} \sqrt{3}}{6} .$

C. $\frac{π a^{3} \sqrt{3}}{12} .$

D. $\frac{π a^{3}}{8} .$

Câu 47:

Cho hàm số y = f(x) có bảng biến thiên như sau

Số điểm cực trị của hàm số

g (x) = f^{3} (x) + 3 f^{2} (x) + 2020

là

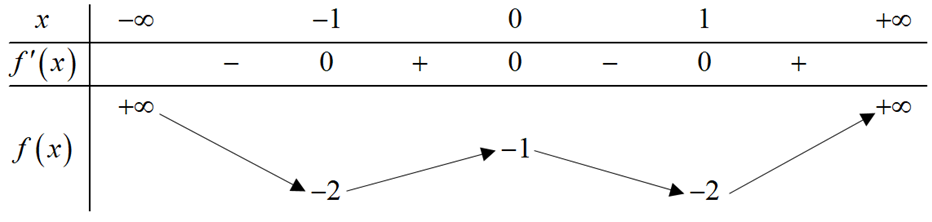
A. 3

B. 7

C. 5

D. 4

Câu 48:

Cho y = f(x) có đồ thị f'(x) như hình vẽ:

Giá trị nhỏ nhất của hàm số

g (x) = f (x) + \frac{1}{3} x^{3} - x

trên đoạn [-1;2] bằng

A. $\frac{2}{3}$

B. $f (- 1) + \frac{2}{3}$

C. $f (2) + \frac{2}{3}$

D. $f (1) - \frac{2}{3}$

Câu 49:

Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng

(- 8; + \infty)

để phương trình

x^{2} + x (x - 1) 2^{x + m} + m = (2 x^{2} - x + m) {.2}^{x - x^{2}}

có nhiều hơn hai nghiĉ̣m phân biệt?

A. 8

B. 6

C. 7

D. 5

Câu 50:

Tìm số các giá tri nguyên của tham số m thuộc khoảng (-20;20) đề hàm số

f (x) = \frac{1}{7} x^{7} + \frac{6}{5} x^{5} - \frac{m^{3}}{4} x^{4} + (5 - m^{2}) x^{3} - 3 m x^{2} + 10 x + 2020

đồng biến trên (0;1)

A. 19

B. 20

C. 21

D. 22

(2023) Đề thi thử Toán THPT Chuyên Vĩnh Phúc có đáp án

Giới thiệu

Liên kết

Chính sách

Kết nối

(2023) Đề thi thử Toán THPT Chuyên Vĩnh Phúc có đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM