(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

Câu 1:

Đạo hàm của hàm số

y = π^{x}

là

A. $y^{'} = π^{x} \ln π$

B. $y^{'} = x π^{x - 1} \ln π$

C. $y^{'} = \frac{π^{x}}{\ln π}$

D. $y^{'} = x π^{x - 1}$

Câu 2:

Đồ thị của hàm số

y = \frac{x - 2}{x + 1}

có đường tiệm cận đứng là

A. x = 2

B. x = -1

C. y = 1

D. y = -2

Câu 3:

Cho hàm số y = f(x) có đạo hàm f'(x) = x(2 - x) . Số điểm cực trị của hàm số y = f(x) là

A. 0

B. 3

C. 1

D. 2

Câu 4:

Cho hàm số y = f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:

Khi đó hàm số y = f(x) đồng biến trên khoảng

A. $(- 1; + \infty)$

B. $(- \infty; 2)$

C. (-1;2)

D. $(- \infty; - 1)$

Câu 5:

Một khối lăng trụ có diện tích đáy bằng B, chiều cao h. Thể tích khối lăng trụ đó bằng

A. $\frac{1}{3} B h$

B. Bh

C. $\frac{1}{2} B h$

D. 3Bh

Câu 6:

Cho

F (x) = \int (e^{x} - 1) d x

. Trong các khẳng định sau, khẳng định nào đúng?

A. $F (x) = e^{x} + C$

B. $F (x) = e^{x} + x + C$

C. $F (x) = e^{x} - x + C$

D. $F (x) = - e^{x} + x + C$

Câu 7:

Số các tổ hợp chập

k, (k \in ℕ)

của một tập hợp có n phần tử

(n \in ℕ^{*}, 0 \leq k \leq n)

là:

A. $C_{n}^{k} = \frac{n!}{k!}$

B. $C_{n}^{k} = \frac{n!}{k! (n - k)!}$

C. $C_{n}^{k} = \frac{n!}{k (n - k)!}$

D. $C_{n}^{k} = \frac{n!}{(n - k)!}$

Câu 8:

Giá trị nhỏ nhất của hàm số y = 1 + x³ trên đoạn [1;2] bằng

A. 9

B. 1

C. 2

D. -7

Câu 9:

Tập xác định D của hàm số

y = {(x - 1)}^{- 2023}

là

A. $D = ℝ \ \{1\}$

B. $D = (- \infty; 1)$

C. $D = ℝ$

D. $D = (1; + \infty)$

Câu 10:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. $y = - x^{4} + 2 x^{2} + 1$

B. $y = - x^{3} + 3 x + 1$

C. $y = x^{4} - 2 x^{2} + 1$

D. $y = x^{2} - 3 x + 1$

Câu 11:

Cho hàm số

f (x) = 3 x^{2} + 1.

Trong các khẳng định sau, khẳng định nào đúng?

A. $\int f (x) d x = \frac{x^{3}}{3} + x + C$

B. $\int f (x) d x = x^{3} + x + C$

C. $\int f (x) d x = x^{3} + C$

D. $\int f (x) d x = x^{3} - x + C$

Câu 12:

Nghiệm của phương trình

3^{x - 1} = 9

là

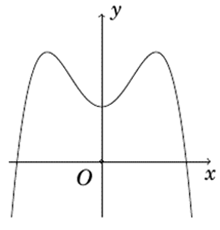
A. x = 1

B. x = -3

C. x = 0

D. x = 3

Câu 13:

Tập nghiệm của bất phương trình

\log (x - 1) \geq 1

là

A. $(11; + \infty)$

B. $[1; + \infty)$

C. $[11; + \infty)$

D. $(- \infty; 11]$

Câu 14:

Trong không gian Oxyz, cho véc tơ

\vec{O A} = - \vec{i} + \vec{j} + 2 \vec{k}

. Khi đó điểm A có toạ độ là

A. (1;-1;-2)

B. (-1;1;-2)

C. (-1;1;2)

D. (1;-1;2)

Câu 15:

Cho cấp số cộng (u_n) có u₁ = -2 và u₂ = 1. Tìm công sai d.

A. d = -1

B. d = 3

C. d = 2

D. d = -3

Câu 16:

Cho

F (x) = \int \sin \frac{x}{2} d x

. Biết

F (π) = 1

. Mệnh đề nào dưới đây đúng?

A. $F (0) \in (2; 3)$

B. $F (0) \in (- 4; - 2)$

C. $F (0) \in (0; 1)$

D. $F (0) \in (- 2; 0)$

Câu 17:

Cho hình chóp S.ABC, đáy ABC là tam giác vuông tại C có AB = 2a, BC = a, cạnh bên SA vuông góc với đáy và

S A = a \sqrt{3}

. Tính thể tích khối chóp S.ABC.

A. $a^{3}$

B. $\frac{2 \sqrt{3}}{3} a^{3}$

C. $\sqrt{3} a^{3}$

D. $\frac{1}{2} a^{3}$

Câu 18:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chóp có đáy là hình thoi luôn có mặt cầu ngoại tiếp.

B. Hình lăng trụ đứng luôn có mặt cầu ngoại tiếp.

C. Hình chóp có đáy là hình thang cân luôn có mặt cầu ngoại tiếp.

D. Hình lăng trụ có đáy là hình chữ nhật luôn có mặt cầu ngoại tiếp.

Câu 19:

Cho hàm số bậc bốn y = f(x) có đồ thị hàm số y = f'(x) là đường cong ở hình bên dưới. Hàm số y = f(x) có bao nhiêu điểm cực trị?

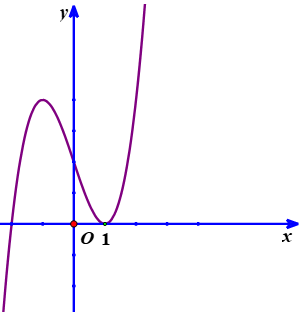
A. 3

B. 2

C. 0

D. 1

Câu 20:

Cho khối chóp tứ giác có đáy là hình vuông và có thể tích V. Nếu tăng độ dài chiều cao của khối chóp đã cho lên gấp ba và giữ nguyên cạnh đáy của nó thì ta được khối chóp mới có thể tích bằng

A. V

B. 9V

C. 3V

D. $\frac{V}{3}$

Câu 21:

Cho các số thực a, b. Biểu thức

A = \log_{2} 2^{a} + \log_{2} 2^{b}

có giá trị bằng

A. a + b

B. ab

C. -ab

D. - a - b

Câu 22:

Số nghiệm nguyên của bất phương trình

\log_{4} (x + 6) < 2 - 2 \log_{4} x

bằng

A. 2

B. Vô số

C. 1

D. 0

Câu 23:

Cho khối trụ có chiều cao h bằng bán kính đáy và thể tích

V = 27 π

. Tính chiều cao h của khối trụ đó.

B. $h = 3 \sqrt[3]{2}$

C. $h = 3 \sqrt{3}$

D. $h = 3 \sqrt[3]{3}$

Câu 24:

Hình chóp S.ABCD có diện tích đáy ABCD bằng a² và độ dài đường cao bằng 6a. Thể tích khối chóp S.ABCD bằng

A. $6 a^{3}$

B. $a^{3}$

C. $3 a^{3}$

D. $2 a^{3}$

Câu 25:

Trong không gian với hệ tọa độ Oxyz, gọi (S) là mặt cầu đi qua hai điểm A(-1;-2;4), B(2;1;2) và có tâm thuộc trục Oz. Bán kính của mặt cầu (S) là

A. R = 6

B. $R = \sqrt{3}$

C. $R = \sqrt{6}$

D. R = 3

Câu 26:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BDD'B') bằng

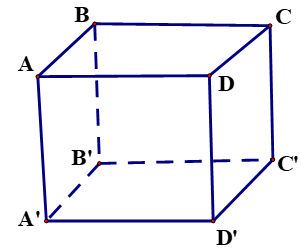
A. a

B. $\frac{a \sqrt{2}}{4}$

C. $\sqrt{2} a$

D. $\frac{a \sqrt{2}}{2}$

Câu 27:

Cho hình nón có độ dài đường sinh bằng 6a và bán kính đáy bằng a. Diện tích xung quanh của hình nón đã cho bằng

A. $12 π a^{2}$

B. $8 π a^{2}$

C. $6 π a^{2}$

D. $2 π a^{2}$

Câu 28:

Chọn khẳng định sai trong các khẳng định sau:

Trong một khối đa diện

A. mỗi mặt có ít nhất 3 cạnh.

B. mỗi đỉnh là đỉnh chung của ít nhất 3 mặt.

C. mỗi cạnh là cạnh chung của đúng 2 mặt.

D. hai mặt bất kì luôn có ít nhất một điểm chung.

Câu 29:

Số đường tiệm cận của đồ thị hàm số

y = \frac{1 + \sqrt{x + 4}}{x^{2} + 5 x}

là

A. 2

B. 0

C. 3

D. 1

Câu 30:

Trên khoảng

(0; + \infty)

, đạo hàm của hàm số

y = \ln \frac{x}{e^{x}}

là

A. $y' = \frac{x}{1 + x}$

B. $y' = \frac{1 - x}{x}$

C. $y' = \frac{1 + x}{x}$

D. $y' = \frac{x}{1 - x}$

Câu 31:

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới.

Số nghiệm thực của phương trình f(x) = 1 là

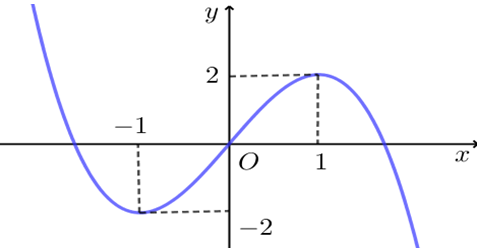
A. 2

B. 3

C. 1

D. 0

Câu 32:

Tìm tất cả các giá trị thực của tham số m để hàm số

y = {(x^{2} + x + m)}^{\frac{1}{3}}

có tập xác định là R

A. $m \leq \frac{1}{4}$

B. $m > \frac{1}{4}$

C. $m \geq \frac{1}{4}$

D. $m < \frac{1}{4}$

Câu 33:

Cho hàm số

y = x^{3} - 3 x + m

(m là tham số thực), thỏa mãn

\underset{[0; 2]}{\min y} = 3.

Mệnh đề nào dưới đây đúng?

A. 7 < m < 20

B. m > 20

C. -10 < m < 6

D. m < -10

Câu 34:

Biết tổng các nghiệm của phương trình

\log_{2} (4^{x} + 48) = x + 4

bằng

a + b \log_{2} 3

với

(a; b \in ℤ)

. Tính 2a + b

A. $2 a + b = 8$

B. $2 a + b = 5$

C. $2 a + b = 9$

D. $2 a + b = 6$

Câu 35:

Cho hàm số y = f(x) có đạo hàm

f' (x) = {(x - 1)}^{2} (x^{2} - 1)

. Hàm số y = f(x) nghịch biến trên khoảng

A. $(- 1; + \infty)$

B. (-1;1)

C. R

D. $(- \infty; - 1)$ và $(1; + \infty)$

Câu 36:

Cho hai hình vuông ABCD, ABEF nằm trong hai mặt phẳng vuông góc với nhau. M là tâm của hình vuông ABEF. Cosin góc giữa hai mặt phẳng (MCD), (EFCD) bằng

A. $\frac{2 \sqrt{5}}{5}$

B. $\frac{\sqrt{10}}{10}$

C. $\frac{3 \sqrt{10}}{10}$

D. $\frac{\sqrt{5}}{5}$

Câu 37:

Có bao nhiêu giá trị nguyên của m để phương trình

2 \log_{2} (x - 3) + (2 m + 5) \log_{\sqrt{x - 3}} 2 = 2 m

có hai nghiệm

x_{1}, x_{2}

thoả mãn

x_{1} < x_{2} < 5

A. 1

B. 4

C. 2

D. 4

Câu 38:

Hội chợ Xuân ở thành phố Vinh có một dãy gồm 15 gian hàng lưu niệm liên tiếp nhau. Một doanh nghiệp X bốc thăm chọn ngẫu nhiên 4 gian hàng trong 15 gian hàng trên để trưng bày sản phẩm. Xác suất để trong 4 gian hàng chọn được của doanh nghiệp X có đúng 3 gian hàng kề nhau bằng

A. $\frac{44}{455}$

B. $\frac{4}{55}$

C. $\frac{22}{455}$

D. $\frac{2}{33}$

Câu 39:

Có bao nhiêu giá trị nguyên của tham số m để hàm số

y = |x^{3} - 3 x^{2} - m|

đạt số điểm cực trị nhiều nhất?

A. 5

B. 3

C. Vô số

D. 4

Câu 40:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới.

Số nghiệm thực phân biệt của phương trình $f [f (x) + 1] + 2 = 0$ là

A. 2

B. 6

C. 4

D. 3

Câu 41:

Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với AB = 2a, BC = a. Biết

\hat{A' A B} = 90^{0}

và

A A' = a \sqrt{5}, C A' = 2 a \sqrt{2} .

Thể tích khối hộp ABCD.A'B'C'D' bằng

A. $a^{3}$

B. $2 a^{3}$

C. $3 a^{3}$

D. $4 a^{3}$

Câu 42:

Cho hàm số bậc ba y = f(x). Hàm số g(x) = f(x + 2) có bảng biến thiên như bên dưới.

Tổng tất cả các giá trị nguyên của tham số m để tập nghiệm của phương trình

\sqrt{4 + m x^{2}} . f [f (x) - m] = 0

có 5 phần tử bằng

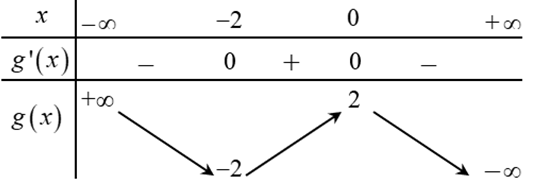
A. 0

B. -3

C. -1

D. 2

Câu 43:

Cho hai khối cầu có tổng diện tích bằng $80 π$ tiếp xúc ngoài nhau và cùng tiếp xúc với mặt phẳng (P) lần lượt tại hai điểm A, B. Tính tổng thể tích của hai khối cầu đó biết $A B = 4 \sqrt{2}$ .

A. $24 \sqrt{2} π$

B. $96 \sqrt{2} π$

C. $96 π$

D. $192 π$

Câu 44:

Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, $\hat{B A C} = 60^{\circ}$ . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B₁, C₁ lần lượt là hình chiếu vuông góc của A trên SB, SC. Đường kính MN thay đổi của mặt cầu (T) ngoại tiếp khối đa diện ABCB₁C₁ và I là điểm cách tâm mặt cầu (T) một khoảng bằng ba lần bán kính. Tính giá trị nhỏ nhất của IM + IN.

A. $6 \sqrt{3}$

B. $\sqrt{20}$

C. 6

D. $2 \sqrt{10}$

Câu 45:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi $(α)$ là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc $φ$ với $\tan φ = \frac{\sqrt{5}}{2}$ . Mặt phẳng $(α)$ chia khối lặp phương thành hai khối đa diện có thể tích là $V_{1}, V_{2}$ với $V_{1} > V_{2}$ . Tính V₁.

A. $V_{1} = \frac{7}{12} a^{3}$

B. $V_{1} = \frac{10}{17} a^{3}$

C. $V_{1} = \frac{7}{24} a^{3}$

D. $V_{1} = \frac{17}{24} a^{3}$

Câu 46:

Cho hàm số y = f(x) thỏa mãn

f (0) = 0, f (x) + f^{'} (x) = 1, \forall x \in ℝ

. Giá trị của f(ln2) bằng

A. 2

B. $\frac{1}{2}$

C. $\frac{1}{\ln 2}$

D. $\ln 2$

Câu 47:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 25; 0)$ sao cho hàm số $y = (x^{4} - 5) e^{x} - m x^{2} - (m^{2} - m) x + 2$ luôn đồng biến trên khoảng $(2; + \infty) ?$

A. 5

B. 24

C. 20

D. 19

Câu 48:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình $4^{2 x - m} - {4.2}^{3 x - 2 m} + {4.2}^{x - m} < 1$ nghiệm đúng với $\forall x \in (- \infty; 4]$ ?

A. 99

B. 92

C. 98

D. 93

Câu 49:

Cho x và y là các số thực. Giá trị nhỏ nhất của biểu thức

P = {(y - 10^{x})}^{2022} + {(e^{y} - x \ln 10)}^{2022}

A. 0

B. 2

C. ${(\frac{5 - \ln 10}{2})}^{2022}$

D. $\frac{3}{2}$

Câu 50:

Trong hệ trục tọa độ Oxyz cho 3 điểm A(5;-2;0), B(4;5;-2) và C(0;3;2). Điểm M di chuyển trên trục Ox. Đặt $Q = 2 |\vec{M A} + \vec{M B} + \vec{M C}| + 3 |\vec{M B} + \vec{M C}|$ . Biết giá trị nhỏ nhất của Q có dạng $a \sqrt{b}$ trong đó $a, b \in ℕ$ và b là số nguyên tố. Tính a + b.

A. 38

B. 23

C. 43

D. 18

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

Giới thiệu

Liên kết

Chính sách

Kết nối

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM