(2023) Đề thi thử Vật Lí THPT Trương Định có đáp án
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Trong dao động điều hòa với tần số góc \(\omega \) và biên độ \(A\), giá trị cực tiểu của vận tốc là
D. \({v_{{\rm{min }}}} = 0\).
Khi một sóng cơ truyền từ không khí vào nước thì đại lượng nào sau đây không thay đổi?
D. Tần số.
Trong các công thức sau, công thức nào dùng để tính tần số dao động nhỏ của con lắc đơn?
D. \(\frac{1}{{2\pi }}\sqrt {\frac{l}{g}} \).
Công thức liên hệ vận tốc truyền sóng \(v\), bước sóng \(\lambda \), chu kì sóng \(T\) và tần số sóng \(f\) là:
D. \(\lambda = v.T = \frac{v}{f}\)
Sóng truyền trên mặt nước có bước sóng \(2\;m\). Quãng đường sóng truyền đi trong một chu kỳ là
D. \(0,5\;m\)
B. môi trường truyền sóng.
D. tần số dao động.
Trong dao động điều hoà, gia tốc biến đổi
B. ngược pha với vận tốc.
D. trễ pha \(\pi /2\) so với vận tốc.
Biên độ dao động cưỡng bức không phụ thuộc vào?
B. Biên độ của ngoại lực cưỡng bức.
Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo có độ cứng k. Con lắc dao động điều hòa với tần số góc là
D. \(\omega = 2\pi \sqrt {\frac{k}{m}} \)
Khi xảy ra hiện tượng giao thoa sóng nước với hai nguồn kết hợp cùng pha \(A,B\). Những điểm trên mặt nước nằm trên đường trung trực của \(AB\) sẽ
B. đứng yên không dao động.
D. dao động với biên độ lớn nhất.
Một con lắc đơn có độ dài \(l\) được thả không vận tốc ban đầu từ vị trí biên có biên độ góc \({\alpha _0}\) \(\left( {\alpha \le {{10}^0}} \right)\). Bỏ qua mọi ma sát. Khi con lắc đi qua vị trí có li độ góc \(\alpha \) thì tốc độ của con lắc là
B. \(v = \sqrt {2gl\left( {\cos \alpha - \cos {\alpha _0}} \right)} \).
D. \(v = \sqrt {2gl(1 - \cos \alpha )} \).
Một con lắc lò xo gồm một lò xo khối lượng không đáng kể, độ cứng k, một đầu cố định và một đầu gắn với một viên bi nhỏ khối lượng m. Chu kỳ biến thiên tuần hoàn của động năng con lắc là
D. \(T = 2\pi \sqrt {\frac{m}{k}} \)
Trong quá trình giao thoa sóng, gọi \(\Delta \varphi \) là độ lệch pha của hai sóng thành phần, với \(n = 0,1\), \(2,3 \ldots \) thì biên độ dao động tổng hợp tại \(M\) trong miền giao thoa đạt giá trị nhỏ nhất khi:
D. \(\Delta \varphi = (2n + 1)\frac{v}{{2f}}\)
Phát biểu nào sau đây không đúng với sóng cơ học?
A. Sóng cơ học có thể lan truyền được trong môi trường chất rắn.
B. Sóng cơ học có thể lan truyền được trong môi trường chân không.
C. Sóng cơ học có thể lan truyền được trong môi trường chất khí.
D. Sóng cơ học có thể lan truyền được trong môi trường chất lỏng.
Nhận định nào sau đây là đúng khi nói về dao động tắt dần?
A. Trong dao động tắt dần, cơ năng tăng dần theo thời gian.
B. Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
C. Lực ma sát càng lớn thì dao động tắt dần càng chậm.
D. Dao động tắt dần có cơ năng không đổi.
Chọn phát biểu đúng khi nói về dao động điều hòa của một vật:
A. Li độ của vật biến thiên theo định luật dạng sin hoặc cosin theo thời gian.
B. Ở vị trí cân bằng gia tốc của vật cực đại.
C. Ở vị trí biên, vận tốc của vật là cực đại.
D. Tần số dao động phụ thuộc cách kích thích dao động.
Lực kéo về tác dụng lên một chất điểm dao động điều hòa có độ lớn:
A. và hướng không đổi.
B. tỉ lệ với bình phương biên độ.
C. không đổi nhưng hướng thay đổi.
D. tỉ lệ với độ lớn của li độ và luôn hướng về vị trí cân bằng.
Cho hai dao động điều hòa cùng phương, cùng tần số \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)\) và \({x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động tổng hợp của hai dao động trên có giá trị
B. \(A = A = \sqrt {A_1^2 + A_2^2 - 2{A_1}{A_2}\cos \frac{{{\varphi _1} + {\varphi _2}}}{2}} \)
D. \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)} \)
Hai nguồn sóng kết hợp tại \({S_1}\) và \({S_2}\) dao động theo phương trình \({u_1} = {u_2} = A\cos \omega t\). Giả sử khi truyền đi biên độ sóng không đổi. Một điểm \(M\) cách \({S_1}\) và \({S_2}\) lần lượt là \({d_1}\) và \({d_2}\). Biên độ dao động tổng hợp tại \(M\) là
D. \({A_M} = A\left| {\cos \frac{{\pi \left( {{d_2} - {d_1}} \right)}}{\lambda }} \right|\)
Ở mặt nước có hai nguồn sóng dao động theo phương vuông góc với mặt nước, có cùng phương trình \(u = A\cos \omega t\). Trong miền gặp nhau của hai sóng, những điểm mà ở đó các phần tử nước dao động với biên độ cực đại sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng
B. một số lẻ lần bước sóng.
D. một số nguyên lần nửa bước sóng.
Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động
A. cùng biên độ và có hiệu số pha không đổi theo thời gian
B. có cùng pha ban đầu và cùng biên độ
C. cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian
D. cùng tần số, cùng phương
Con lắc lò xo dao động điều hoà, khi tăng khối lượng của vật 4 lần thì tần số dao động của vật
D. tăng 2 lần.
Một vật dao động điều hòa theo phương trình \(x = 6\sin 4\pi t(cm)\). Gia tốc của vật lúc \(t = 5\;s\) là
D. 0.
Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t của một vật dao động điều hòa. Biên độ dao động của vật là
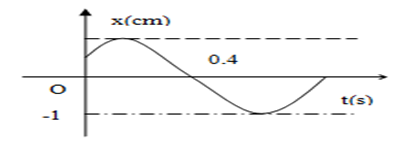
D. 1,0 mm
Con lắc lò xo gồm vật \(m = 100\;g\) và lò xo có độ cứng \(k = 100\;N/m\), ( cho \({\pi ^2} = 10\) ) dao động điều hòa với chu kì
D. \(T = 0,4\;s\)
Một vật thực hiện đồng thời hai dao động: \({x_1} = 8\cos 4t(\;cm)\); \({x_2} = 4\cos (4t + \pi )(cm)\). Pha ban đầu của dao động tổng hợp là:
D. 0
Cho một sóng ngang có phương trình sóng là \(u = 8\sin 2\pi \left( {\frac{t}{{0,1}} - \frac{x}{{50}}} \right)mm\), trong đó \(x\) tính bằng \(cm\), \(t\) tính bằng giây. Bước sóng là
D. \(\lambda = 8\;mm\).
Một con lắc đơn dao động điều hòa tại nơi có \(g = {\pi ^2}\;m/{s^2}\) thì người ta đo được chu kì của nó là \(T = 1\) giây. Chiều dài của con lắc là
D. \(10\;cm\)
Hai con lắc đơn có chu kỳ dao động nhỏ là \({T_1} = 2\;s\) và \({T_2} = 3\;s\). Chu kỳ dao động nhỏ của con lắc đơn có chiều dài bằng tổng chiều dài của hai con lắc trên là
D. \(T = 5\;s\)
Một con lắc lò xo gồm lò xo nhẹ có độ cứng \(50\;N/m\) và vật nhỏ có khối lượng \(200\;g\) đang dao động điều hòa theo phương ngang. Lấy \({\pi ^2} = 10\). Tần số dao động của con lắc là:
D. \(2,5\;Hz\)
Hai dao động điều hòa cùng phương có phương trình lần lượt là \({x_1} = 4\cos \left( {\pi t - \frac{\pi }{6}} \right)cm\) và \({x_2} = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\). Dao động tổng hợp của hai dao động này có biên độ là:
D. \(2\sqrt 3 \;cm\)
Con lắc lò xo dao động điều hòa với tần số góc \(10rad/s\). Lúc \(t = 0\), hòn bi của con lắc đi qua vị trí có li độ \(x = 4\;cm\) với vận tốc \(v = - 40\;cm/s\). Phương trình dao động của con lắc là
B. \(x = 8\cos \left( {10r + \frac{{3\pi }}{4}} \right)(cm)\).
D. \(x = 4\sqrt 2 \cos 10t(\;cm)\).
Dao động tại hai điểm \({S_1},{S_2}\) cách nhau \(10\;cm\) trên mặt chất lỏng có cùng biểu thức \(u = \) \({\mathop{\rm acos}\nolimits} 40\pi t\). Tốc độ truyền sóng trên mặt chất lỏng là \(40\;cm/s\). Trong khoảng \({S_1}\;{S_2}\), số điểm dao động với biên độ cực đại là
Một con lắc lò xo treo thẳng đứng có vật nặng khối lượng \(m = 100\;g\) đang dao động điều hòa. Vận tốc cực đại của vật là \(31,4\;cm/s\) và gia tốc cực đại của vật là \(4\;m/{s^2}\). Lấy \(\pi = 3,14\) và \({\pi ^2} = 10\). Độ cứng của lò xo bằng:
D. \(6,25\;N/m\)
Sóng cơ có tần số \(80\;Hz\) lan truyền trong một môi trường với vận tốc \(4\;m/s\). Dao động của các phần tử vật chất tại hai điểm trên một phương truyền sóng cách nguồn sóng những đoạn lần lượt \(31\;cm\) và \(33,5\;cm\), lệch pha nhau góc
D. \(\pi rad\).
Tại một nơi có hai con lắc đơn dao động với biên độ nhỏ. Trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 5 dao động toàn phần, con lắc thứ hai thực hiện được 4 dao động toàn phần. Tổng chiều dài hai con lắc là \(164\;cm\). Chiều dài mỗi con lắc lần lượt là
B. \({\ell _1} = 100\;cm,{\ell _2} = 64\;cm\)
D. \({\ell _1} = 72,9\;cm,{\ell _2} = 91,1\;cm\)
Trong một thí nghiệm giao thoa sóng trên mặt nước, có hai nguồn kết hợp A và B dao động cùng pha với tần số \(f = 20\;Hz\), cách nhau 8 cm. Tốc độ truyền sóng trên mặt nước \(v = 30\;cm/s\). Gọi C và D là hai điểm trên mặt nước sao cho ABCD là hình vuông. Số điểm dao động với biên độ cực đại trên đoạn CD là
D. 3 điểm.
Một con lắc lò xo nằm ngang gồm lò xo có độ cứng \(k = 100N/m\), vật có khối lượng \(m = 400g\), hệ số ma sát giữa vật và giá đỡ là \(\mu = 0,1\). Từ vị trí cân bằng vật đang nằm yên và lò xo không biến dạng người ta truyền cho vật vận tốc \(v = 100cm/s\) theo chiều làm cho lò xo giảm độ dãn và dao động tắt dần. Độ nén cực đại của vật là bao nhiêu?
D. 5,94 cm
Một con lắc đơn dây treo dài \({\rm{20}}(\;cm)\). Cho \(g = 9,8\left( {\;m/{s^2}} \right)\). Từ vị trí cân bằng kéo con lắc về phía trái một góc \(0,1(rad)\), rồi truyền cho nó một vận tốc \(14(\;cm/s)\) hướng về phía phải. Chọn gốc thời gian là lúc truyền vận tốc, trục tọa độ trùng quỹ đạo dao động, chiều dương hướng từ trái sang phải, gốc tọa độ là vị trí cân bằng. Phương trình dao động có dạng
B. \(s = 2\sqrt 2 \cdot \cos \left( {7t + \frac{\pi }{4}} \right)\quad (cm)\)
D. \(s = 2\sqrt 2 \cdot \cos \left( {7t - \frac{\pi }{4}} \right)\quad (cm)\)
Hai vật A và B có cùng khối lượng \(1kg\) và có kích thước nhỏ được nối với nhau bởi sợi dây mảnh nhẹ dài 10 cm, hai vật được treo vào lò xo có độ cứng \(k = 100N/m\) tại nơi có gia tốc trọng trường \(g = 10m/{s^2}\). Lấy \({\pi ^2} = 10\). Khi hệ vật và lò xo đang ở vị trí cân bằng đủ cao so với mặt đất, người ta đốt sợi dây nối hai vật và vật B sẽ rơi tự do còn vật A sẽ dao động điều hòa theo phương thẳng đứng. Lần đầu tiên vật A lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng
D. 20 cm.