30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 10)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Đồ thị sau đây là đồ thị của hàm số nào?
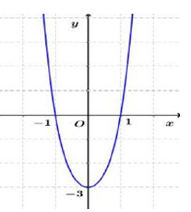
A.
B.
C.
D.
Xét hàm số trên . Chọn khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
B. Hàm số có giá trị nhỏ nhất bằng và giá trị lớn nhất bằng
C. Hàm số không có giá trị nhỏ nhất và giá trị lớn nhất bằng
D. Hàm số có giá trị nhỏ nhất bằng
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số . Khi đó có bao nhiêu số nguyên dương nằm giữa m, M?
A. 1
B. 5
C. 7
D. 0
Cho vuông tại A có . Biết độ dài BC = 10 thì giá trị a nằm trong khoảng nào dưới đây
A. (2;4)
B. (3;5)
C. (4;7)
D. (7;8)
Cho đồ thị hàm số và như hình vẽ. Khẳng định nào sau đây đúng?
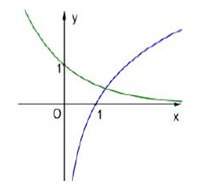
A.
B. 0 < a < 1 < b
C. 0 < b < 1 < a
D.
Cho a là số thực dương, tính tích phân theo a
A.
B.
C.
D.
Cho phương trình trên tập họp số phức . Nếu phương trình nhận số phức làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
B. Mọi hình hộp chữ nhật đều có mặt cầu ngoại tiếp.
C. Mọi hình hộp có một mặt bên vuông góc với đáy đều có mặt cầu ngoại tiếp.
D. Mọi hình hộp đều có mặt cầu ngoại tiếp.
Trong không gian với hệ tọa độ cho 2 điểm A,B thỏa mãn và . Tìm tọa độ trung điểm M của đoạn thẳng AB
A.
B.
C. M(3;4;-2)
D.
Trong không gian với hệ tọa độ Oxyz , cho điểm M(-4; 0;0) và đường thẳng . Gọi H(a;b;c) là hình chiếu của M lên . Tính
A. 5
B. -1
C. -3
D. 7
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R
A.
B.
C.
D.
Hàm số đạt cực tiểu tại x = 2 khi
A. m = 0
B. m > 4
C.
D.
Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số tiếp xúc với parabol
A. m = 7
B.
C. m = 4
D. với mọi
Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm
A.
B.
C.
D.
Cho phương trình (1). Khi đó phương trình (1) tương đương với phương trình nào dưới đây?
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên bằng
A.
B.
C.
D.
Biết , với m,n là các số nguyên. Tính
A. S = 1
B. S = 4
C. S = -5
D. S = -1
Biết . Tính giá trị của
A.
B.
C.
D.
Với các số phức tùy ý, khẳng định nào sau đây sai?
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức , M’ là điểm biểu diễn cho số phức . Tính diện tích tam giác OMM’.
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, . Góc giữa (SBC ) và (ABC) bằng. Thể tích của khối chóp S.ABC là.
A.
B.
C.
D.
Cho đa diện H biết rằng mỗi mặt của H đều là những đa giác có số canh lẻ và tồn tại ít nhất một mặt có số canh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau?
A. Tổng số các cạnh của (H) bằng 9
B. Tổng số các đỉnh của (H) bằng 5
C. Tổng số các cạnh của (H) là một số lẻ
D. Tổng số các mặt của (H) là một số chẵn
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng và đường thẳng . Gọi là đường thẳng nằm trong (P), cắt và vuông góc với d. Hệ phương trình nào là phương trình tham số của ?
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz , cho (P) là mặt phẳng qua đường thẳng và tiếp xúc với mặt cầu . Khi đó (P) song song với mặt phẳng nào sau đây?
A.
B.
C.
D. đáp án khác
Từ các số 1,2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa điều kiện. sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị.
A. 104
B. 106
C. 108
D. 36
Cho . Biết rằng tồn tại số nguyên sao cho .Tính n = ?.
A. 10
B. 11
C. 20
D. 22
Tìm tập xác định của hàm số sau
A.
B.
C.
D.
Trong mặt phăng Oxy, cho phép biến hình f xác định như sau. Với mỗi M (x; y), ta có sao cho M'(x';y') thỏa mãn , với a, b là các hằng số thực. Khi đó a và b nhận giá trị nào trong các giá trị sau đây thì f trở thành phép biến hình đồng nhất?
A. a = b = 1
B. a = 0; b = 1
C. a = 1; b = 2
D. a = b = 0
Một xưởng in có 15 máy in được cài đặt tự động và giám sát bởi một kĩ sư, mỗi máy in có thể in được 30 ấn phẩm trong 1 giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho 1 đợt hàng là 48 000 đồng, chi phí trả cho kĩ sư giám sát là 24 000 đồng/ giờ. Đợt hàng này xưởng nhận in 6000 ấn phẩm thì số máy in cần sử dụng để chi phi in ít nhất là
A. 10 máy
B. 11 máy
C. 12 máy
D. 9 máy
Cho hàm số . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị đến một tiếp tuyến của . Giá trị lớn nhất d có thể đạt được là.
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi x thuộc
A. 1
B. 2
C. 2018
D. vô số
Cho hàm số . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Tính tích phân , ta được
A.
B.
C.
D.
Cho hàm số có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox

A.
B.
C.
D. Đáp án khác
Cho số phức z thỏa mãn . Tìm giá trị lớn nhất của
A.
B.
C.
D.
Hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, ,SC tạovới mặt đáy một góc . Mặt cầu ngoại tiếp hình chóp S.ABCD có bán kính bằng . Thể tích khối chóp S.ABCD bằng.
A.
B.
C.
D.
Cho hình nón đỉnh S, đáy là đường tròn (O; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho . Tính khoảng cách từ O đến (SAB).
A.
B.
C.
D.
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai mặt phẳng
. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
A.
B.
C.
D.
Cho hàm số . Có bao nhiêu giá trị thực của tham số m để hàm số liên tục trên R?
A. 2
B. 0
C. 6
D. vô số
Hàm số đạt giá trị lớn nhất là
A.
B.
C.
D.
Cho hai đường thẳng song song nhau. Trên có 6 điểm tô màu đỏ, trên có 4 điểm tô màu xanh. Chọn ngẫu nhiên 3 điểm bất kì trong các điểm trên. Tính xác suất để 3 điểm được chọn lập thành tam giác có 2 đỉnh tô màu đỏ.
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m để điểm tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số một tam giác có diện tích nhỏ nhất.
A. 0
B. 1
C. 2
D. Không tồn tại
Có bao nhiêu giá trị thực của tham số m để phương trình có duy nhất 1 nghiệm thực.
A. 1
B. 0
C. 2
D. Vô số
Để kỷ niệm ngày 26-3. Chi đoàn 12A dư định dưng một lều trại có dạng parabol (nhìn từ mặt trước, lều trại được căng thẳng từ trước ra sau, mặt sau trại cũng là parabol có kích thước giống như mặt trước) với kích thước. nền trại là một hình chữ nhật có chiều rộng là 3 mét, chiều sâu là 6 mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía trong trại để lớp 12A cử số lượng người tham dư trại cho phù hợp.
A. 30 m3
B. 36 m3
C. 40 m3
D. 41 m3
Cho tứ diện đều ABCD có độ dài canh bằng 1. Gọi M, N là hai điểm thuộc các canh AB, AC sao cho mặt phẳng (DMN) vuông góc với mặt phẳng (ABC). Đặt . Tìm x; y để diện tích toàn phần của tứ diện DAMN nhỏ nhất.
A.
B.
C.
D.
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với và . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
A.
B.
D.
D.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng , mặt phẳng . Gọi M là giao điểm của d và (P). Gọi M là đường thẳng nằm trong (P) vuông góc với d và cách M một khoảng bằng . Phương trình đường thẳng là.
A.
B.
C.
D. đáp án khác
Cho dãy số xác định bởi . Tính tổng
A.
B.
C.
D.
Xét 3 điểm A, B, C của mặt phẳng phức theo thứ tự biểu diễn 3 số phức phân biệt thỏa mãn . Nếu thì tam giác ABC có đặc điểm gì ?
A. cân
B. vuông
C. có góc
D. đều