30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 24)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho . Tính
A. 5
B. 3
C. 2
D. 4
Tập nghiệm của phương trình là
A.
B.
C.
D.
Gọi là hai nghiệm nguyên dương của bất phương trình . Tính giá trị của biểu thức
A. P = 3
B. P = 4
C. P = 5
D. P = 6
Điểm biểu diễn của số phức z là M(1;2). Tìm tọa độ điểm biểu diễn của số phức
A. (-1;6)
B. (2;-3)
C. (2;1)
D. (2;3)
Tìm nguyên hàm F(x) của hàm số biết
A.
B.
C.
D.
Tính
A. 4
B. -1
C.
D. 2
Cho m là một số thực. Số nghiệm của phương trình là
A. Không xác định
B. 0
C. 1
D. 2
Với cách biến đổi thì tích phân trở thành
A.
B.
C.
D.
Cho n là số nguyên dương sao cho tổng các hệ số trong khai triển của bằng 1024. Hệ số của trong khai triển đó bằng
A.
B. 90
C. 45
D. 80
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp có tọa độ các điểm . Giả sử tọa độ điểm A'(x;y;z) thì bằng
A. 2
B. -3
C. 7
D. 5
Giá trị lớn nhất M của hàm số trên đoạn là:
A. M = 1
B. M = 5
C. M = 3
D. M = 7
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng . Gọi H(x,y,z) là hình chiếu của O lên mặt phẳng (P) thì bằng
A. 0
B. 2
C. 1
D. 3
Với các số dương a,b bất kì, đặt . Mệnh đề nào dưới đây là đúng?
A.
B.
C.
D.
Hàm số nào sau đây có đồ thị phù hợp hình vẽ?
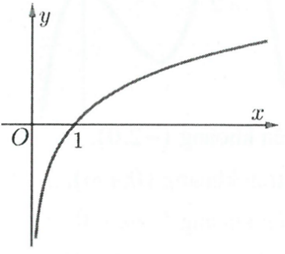
A.
B.
C.
D.
Cho hàm số . Tính
A.
B.
C.
D.
Cho số phức z thỏa mãn . Tìm giá trị lớn nhất của |z|:
A.
B.
C.
D.
Người ta viết thêm 999 số thực vào giữa số 1 và số 2018 để được một cấp số cộng có 1001 số hạng. Tính số hạng thứ 501.
A. 1009
B.
C. 1010
D.
Cho hình tròn (C), bán kính R = 2. Cắt hình tròn (C) (như hình vẽ), rồi lấy hình tròn đó dán kín OA và OB lại để tạo ra mặt xung quanh của một hình nón. Tính diện tích toàn phần của hình nón.
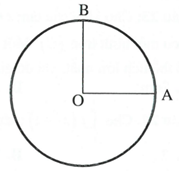
A.
B.
C.
D.
Cho hàm số y = f(x) xác định, liên tục trên R và có đạo hàm f'(x). Biết rằng hàm số f'(x) có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
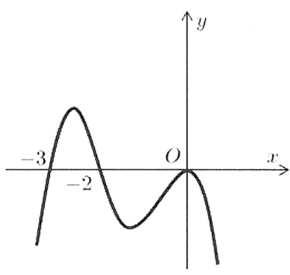
A. Hàm số đồng biến trên khoảng (-2;0)
B. Hàm số nghịch biến trên khoảng
C. Hàm số đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng (-3;-2)
Cho hàm số (1) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của tham số thực m lớn hơn -10 để hàm số (1) đồng biến trên khoảng
A. 5
B. 4
C. 6
D. 7
Đặt (S) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số , trục hoành và đường thẳng . Tìm giá trị của tham số m để
A. 2
B. 3
C. 4
D. 1
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
Cho khối cầu tâm (O) bán kính 6cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, khi đó giá trị của x là:
A. 2 cm
B. 3 cm
C. 4 cm
D. 0 cm
Cho . Khi đó bằng:
A. 2
B. 1
C. -1
D.. 4
Cho a, b là hai số thực sao cho hàm số liên tục trên R. Tính a - b.
A. 0
B. -1
C. -5
D. 7
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm . Có bao nhiêu mặt phẳng qua O và cách đều ba điểm A, B, C?
A. 4 mặt phẳng.
B. 1 mặt phẳng.
C. 2 mặt phẳng.
D. Có vô số mặt phẳng.
Có bao nhiêu giá trị nguyên m để hàm số đồng biến trên R?
A. 5
B. 4
C. 3
D. Vô số
Cho hình chóp đỉnh S có đường cao và bán kính đáy bằng a. Biết đường tròn đáy của hình nón nội tiếp trong hình thang cân ABCD với AB//CD và , hãy tính theo a thể tích khối chóp S.ABCD.
A.
B.
C.
D.
Tìm điểm M thuộc sao cho qua M kẻ được duy nhất một tiếp tuyến tới (C).
A. (1;3)
B. (0;-1)
C. (-1;2)
D. (-1;1)
Hình nón (N) có đường sinh bằng 2a. Thể tích lớn nhất của khối nón (N) là:
A.
B.
C.
D.
Cho hàm số . Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số có cực tiểu mà không có cực đại. Tính tổng các phần tử của tập S.
A. 1
B. 2
C. 6
D. 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và đường thẳng . Gọi là một đường thẳng chứa trong (P), cắt và vuông góc với d. Véc tơ là một véc tơ chỉ phương của . Tính tổng S = a + b.
A. S = 1
B. S = 0
C. S = 2
D. S = 4
Cho hai số thực a, b thỏa mãn . Tập giá trị của là:
A. [0;2]
B.
C.
D.
Thầy Hùng vay ngân hàng 100 triệu đồng, với lãi suất 1,1% /tháng. Thầy muốn hoàn nợ cho ngân hàng theo cách: sau đúng một tháng kể từ ngày vay, anh bắt đầu hoàn nợ, và những lần tiếp theo cách nhau đúng một tháng. Số tiền hoàn nợ ở mỗi lần là như nhau và trả hết nợ sau đúng 18 tháng kể từ ngày vay. Hỏi theo cách đó, số tiền lãi mà thầy Hùng ĐZ phải trả là bao nhiêu (làm tròn đến kết quả hàng nghìn)? Biết rằng, lãi suất ngân hàng không thay đổi trong suốt thời gian mà thầy vay.
A. 10773700 đồng.
B. 10773000 đồng.
C. 10774000 đồng.
D. 10773800 đồng.
Cho a, x là các số thực dương và thỏa mãn . Tìm giá trị lớn nhất của a?
A. 1
B.
C.
D.
Cho hình trụ (T) có hai đường tròn đáy O và O'. Một hình vuông ABCD nội tiếp trong hình trụ (trong đó các điểm ). Biết hình vuông ABCD có diện tích bằng . Tìm thể tích lớn nhất của khối trụ (T).
A.
B.
C.
D.
Parabol chia hai đường tròn có tâm tại gốc tọa độ, bán kính bằng thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào trong các khoảng sau đây?
A. (0,4;0,5)
B. (0,5;0,6)
C. (0,6;0,7)
D. (0,7;0,8)
Biểu đồ bên cho thấy kết quả thống kê sự tăng trưởng về số lượng của một đàn vi khuẩn; cứ sau 12 tiếng thì số lượng của một đàn vi khuẩn tăng lên gấp 2 lần. Số lượng vi khuẩn ban đầu của đàn là 250 con. Công thức nào dưới đây thể hiện sự tăng trưởng về số lượng của đàn vi khuẩn tại thời điểm t?
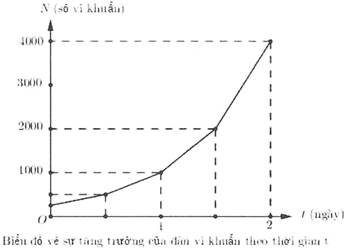
A.
B.
C.
D.
Cho mặt cầu (S) bán kính . Mặt phẳng cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng . Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A.
B.
C.
D.
Cho dãy số thỏa mãn điều kiện và . Đặt . Tìm số tự nhiên n nhỏ nhất thỏa mãn
A. 2587
B. 2590
C. 2593
D. 2584
Cho số phức z thỏa mãn: và nhỏ nhất. Mô đun của số phức z bằng:
A. 6
B. 7
C. 5
D. 8
Cho hàm số xác định, có đạo hàm trên đoạn [0;1] và thỏa mãn . Tính
A.
B.
C.
D. 505
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và mặt phẳng . Biết mặt phẳng (P) chứa và cách O một khoảng lớn nhất. Tổng bằng
A. 1
B. 3
C. 2
D. -1
Cho số phức thỏa mãn đồng thời hai điều kiện và biểu thức đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b bằng
A. -1
B. 2
C. -2
D. 1
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, . Điểm H nằm trên cạnh AB thỏa mãn , hai mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng đáy. Cosin góc giữa SD và (SBC) bằng
A.
B.
C.
D.
Cho phương trình , m là tham số thực. Có bao nhiêu giá trị nguyên của để phương trình có nghiệm?
A. 2015
B. 2016
C. 2018
D. 2017
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;2] thỏa mãn điều kiện và . Tích phân bằng
A.
B.
C.
D.
Tại trạm xe khách có 5 hành khách đang chờ xe đón, không ai quen nhau trong đó có anh A và chị B. Khi đó có 1 chiếc xe ghé trạm đón khách, biết rằng lúc đó trên xe chỉ còn đúng 5 ghế trống, mỗi ghế trống chỉ 1 người ngồi gồm có 1 dãy ghế trống 3 chỗ và 2 chỗ ghế đơn để chở 5 người. Tham khảo hình vẽ bên các ghế trống được ghi là (1) , (2), (3), (4), (5) và 5 hành khách lên ngồi ngẫu nhiên vào 5 chỗ trống. Xác suất để anh A và chị B ngồi cạnh nhau bằng

A.
B.
C.
D.
Cho x, y là các số dương . Giá trị nhỏ nhất của là . Tích ab bằng
A. 115
B. 45
C. 108
D. 81