35 đề minh họa THPT Quốc gia môn Toán năm 2022 có lời giải (Đề 11)

Câu 1:

Có bao nhiêu cách chọn 3 học sinh từ một nhóm gồm 8 học sinh?

A. $A_{8}^{3}$ .

B.

3^{8}

.

C.

8^{3}

.

D.

C_{8}^{3}

.

Câu 2:

Cho cấp số cộng $(u_{n})$ với $u_{17} = 33$ và $u_{33} = 65$ thì công sai bằng

A. 1

B. 3

C. -2

D. 2

Câu 3:

Cho hàm số $y = f (x)$ có bảng biến thiên dưới đây

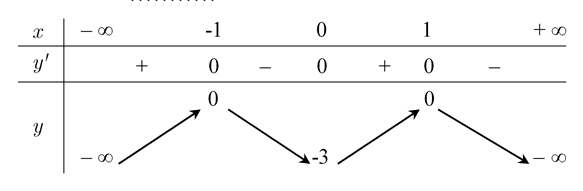
Hỏi hàm số đồng biến trên khoảng nào dưới đây?

A. $(- 1; 0)$ .

B.

(- 1; 1)

.

C.

(- \infty; 0)

.

D.

(- \infty; - 1)

.

Câu 4:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Giá trị cực đại của hàm số là:

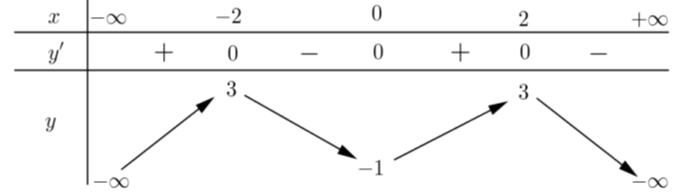
A. -1

B. 0

C. 2

D. 3

Câu 5:

Cho hàm số $f (x)$ có đạo hàm $f^{'} (x) = x {(x - 1)}^{2} {(x - 2)}^{5} {(x - 3)}^{7}$ . Số điểm cực trị của hàm số đã cho là

A. 3

B. 1

C. 4

D. 2

Câu 6:

Tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 1}{x - 1}$ là

A. y = -1.

B. y = 1.

C.

y = \frac{1}{2}

.

D. y = 2.

Câu 7:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. $y = - x^{4} + 2 x^{2}$ .

B.

y = x^{2} - 2 x + 1

.

C.

y = x^{3} - 3 x + 1

.

D.

y = - x^{3} + 3 x + 1

.

Câu 8:

Đường thẳng y = -3x cắt đồ thị hàm số $y = x^{3} - 2 x^{2} - 2$ tại điểm có tọa độ $(x_{0}; y_{0})$ thì

A.

y_{0} = 3

.

B.

y_{0} = - 3

.

C.

y_{0} = 1

.

D.

y_{0} = - 2

.

Câu 9:

Với a,b là hai số thực dương tùy ý, $\log_{3} (a^{3} \sqrt{b})$ bằng

A. $\frac{3}{2} \log_{3} (a b) .$

B.

\frac{3}{2} \log_{3} (a + b) .

C.

3 \log_{3} a + \frac{1}{2} \log_{3} b .

D.

3 \log_{3} a + 2 \log_{3} b

.

Câu 10:

Hàm số

y = 3^{x^{2} - x}

có đạo hàm là

A. $(2 x - 1) {.3}^{x^{2} - x} . \ln 3$ .

B. $(2 x - 1) {.3}^{x^{2} - x}$ .

C.

3^{x^{2} - x} . \ln 3

.

D.

(x^{2} - x) {.3}^{x^{2} - x - 1}

.

Câu 11:

Cho $x, y > 0$ và $α, β \in ℝ$ . Khẳng định nào sau đây sai?

A. ${(x^{α})}^{β} = x^{α β}$ .

B.

x^{α} + y^{α} = {(x + y)}^{α}

.

C.

x^{α} . x^{β} = x^{α + β}

.

D.

{(x y)}^{α} = x^{α} . y^{α}

.

Câu 12:

Phương trình $3^{x^{2} - 2 x} = 1$ có nghiệm là

A. x = 0, x = 2.

B. x = -1, x = 3.

C. x = 0, x = -2.

D. x = 1, x = -3.

Câu 13:

Nghiệm của phương trình $\log_{2} (x + 9) = 5$ là

A. x = 41.

B. x = 16.

C. x= 23.

D. x = 1.

Câu 14:

Tìm nguyên hàm của hàm số

f (x) = 4 x^{3} + 2 x

.

A. $\int f (x) d x = 12 x^{2} + x^{2} + C$ .

B.

\int f (x) d x = \frac{4}{3} x^{4} + x^{2} + C

.

C.

\int f (x) d x = 12 x^{2} + 2 + C

.

D.

\int f (x) d x = x^{4} + x^{2} + C

.

Câu 15:

Tìm họ nguyên hàm của hàm số

f (x) = e^{2 x + 1}

A. $\int f (x) d x = 2 e^{2 x + 1} + C$ .

B.

\int f (x) d x = e^{x^{2} + x} + C

.

C.

\int f (x) d x = \frac{1}{2} e^{2 x + 1} + C

.

D.

\int f (x) d x = e^{2 x + 1} + C

.

Câu 16:

Cho $\int_{0}^{1} f (x) d x = 3$ và $\int_{1}^{3} f (x) d x = - 2$ . Tính $\int_{0}^{3} f (x) d x$ .

A. 5

B. 1

C. -5

D. -1

Câu 17:

Tính tích phân

I = \int_{1}^{2} (2 x - 1) d x

.

A.

I = \frac{5}{6}

.

B. I = 3.

C. I = 1.

D. I = 2.

Câu 18:

Cho số phức

z = - 5 + 2 i

. Phần thực và phần ảo của số phức

\bar{z}

lần lượt là

A. 5 và -2.

B. 5 và 2.

C. -5 và 2.

D. -5 và -2.

Câu 19:

Cho hai số phức $z_{1} = - 2 - 3 i$ và $z_{2} = 5 - i$ . Tổng phần thực và phần ảo của số phức $2 z_{1} - z_{2}$ bằng

A. 13

B. -14

C. -6

D. 3

Câu 20:

Trên mặt phẳng tọa độ, cho số phức z thỏa mãn

\bar{z} = 3 i - 1

, điểm biểu diễn số phức z là

A. $Q (3; - 1)$

B.

P (- 1; - 3)

C.

N (1; - 3)

D.

M (- 1; 3)

.

Câu 21:

Cho khối chóp có diện tích đáy $B = 6 a^{2}$ và chiều cao $h = 2 a$ . Thể tích khối chóp đã cho bằng:

A.

12 a^{3}

.

B.

2 a^{3}

.

C.

4 a^{3}

.

D.

6 a^{3}

.

Câu 22:

Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6. Thể tích của khối hộp đã cho bằng

A. 8

B. 16

C. 48

D. 12

Câu 23:

Thể tích khối nón có chiều cao h , bán kính đường tròn đáy r là

A. $V = \frac{1}{2} π r^{2} h$ .

B.

V = π r^{2} h

.

C.

V = \frac{4}{3} π r^{2} h

.

D.

V = \frac{1}{3} π r^{2} h

.

Câu 24:

Cho khối nón có thể tích

V = 4 π

và bán kính đáy r = 2. Tính chiều cao h của khối nón đã cho.

A. h = 3.

B. h = 1.

C.

h = \sqrt{6}

.

D. h = 6.

Câu 25:

Trong không gian với hệ tọa độ $O x y z$ , cho $A (- 1; 2; - 3)$ và $B (- 3; - 1; 1)$ . Tọa độ của $\vec{A B}$ là

A. $\vec{A B} = (- 2; - 3; 4)$ .

B.

\vec{A B} = (4; - 3; 4)

.

C.

\vec{A B} = (- 4; 1; - 2)

.

D.

\vec{A B} = (2; 3; - 4)

.

Câu 26:

Trong không gian $O x y z$ , cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 4 x + 2 y - 6 z + 1 = 0$ . Tọa độ tâm I của mặt cầu là

A. $I (4; - 2; 6)$ .

B.

I (2; - 1; 3)

.

C.

I (- 4; 2; - 6)

.

D.

I (- 2; 1; - 3)

.

Câu 27:

Trong không gian với hệ tọa độ

O x y z

, điểm

M (- 2; 1; - 1)

thuộc mặt phẳng nào sau đây?

A. $- 2 x + y - z = 0$ .

B.

x + 2 y - z - 1 = 0

.

C.

2 x - y - z + 6 = 0

.

D.

- 2 x + y - z - 4 = 0

.

Câu 28:

Trong không gian $O x y z$ , cho đường thẳng $d : \frac{x - 3}{2} = \frac{y - 4}{- 5} = \frac{z + 1}{3}$ . Vecto nào dưới đây là một vecto chỉ phương của d?

A.

\vec{u_{2}} = (2; 4; - 1)

.

B.

\vec{u_{1}} = (2; - 5; 3)

.

C.

\vec{u_{3}} = (2; 5; 3)

.

D.

\vec{u_{4}} = (3; 4; 1)

.

Câu 29:

Chọn ngẫu nhiên 3 bóng từ hộp gồm 5 bóng xanh và 3 bóng vàng. Tính xác suất lấy được 3 bóng cùng màu?

A.

\frac{11}{56}

.

B.

\frac{5}{28}

.

C.

\frac{1}{7}

.

D.

\frac{56}{11}

.

Câu 30:

Hàm số $y = \frac{2}{3 x^{2} + 1}$ nghịch biến trên khoảng nào dưới đây?

A.

(- 1; 1)

.

B.

(- \infty; 0)

.

C.

(- \infty; + \infty)

.

D.

(0; + \infty)

.

Câu 31:

Giá trị nhỏ nhất của hàm số $y = x^{4} + 2 x^{2} - 1$ trên đoạn $[- 1; 2]$ là.

A. -1

B. 2

C. 1

D. -2

Câu 32:

Số nghiệm nguyên của bất phương trình ${(\frac{1}{3})}^{2 x^{2} - 3 x - 7} > 3^{2 x - 21}$ là

A. 7

B. 6

C. Vô số

D. 8

Câu 33:

Cho $\int_{0}^{1} f (x) d x = 2$ và $\int_{0}^{1} g (x) d x = 5$ . Tính $\int_{0}^{1} (f (x) - 2 g (x)) d x$ .

A. -8

B. 12

C. 1

D. -3

Câu 34:

Tìm môđun của số phức $z = 3 - 2 i$ .

A.

|z| = 5

.

B.

|z| = \sqrt{5}

.

C.

|z| = 13

.

D.

|z| = \sqrt{13}

.

Câu 35:

Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, $A B = a$ , $B C = 2 a$ , SA vuông góc với mặt phẳng đáy và $S A = \sqrt{15} a$ . Media VietJack

Góc giữa đường thẳng SC và mặt phẳng đáy bằng

A.

45 °

.

B.

30 °

.

C.

60 °

.

D.

90 °

.

Câu 36:

Cho hình chóp $S . A B C D$ có $S A ⊥ (A B C D)$ , đáy ABCD là hình chữ nhật. Biết $A D = 2 a$ , $S A = a$ . Khoảng cách từ A đến $(S C D)$ bằng

A.

\frac{3 a}{\sqrt{7}}

.

B.

\frac{3 a \sqrt{2}}{2}

.

C.

\frac{2 a}{\sqrt{5}}

.

D.

\frac{2 a \sqrt{3}}{3}

.

Câu 37:

Trong không gian $O x y z$ , cho hai điểm $I (1; 1; 1)$ và $A (1; 2; 3)$ . Phương trình mặt cầu có tâm I và đi qua A là

A. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 29$ .

B.

{(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 25

.

C.

{(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5

.

D.

{(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 5

.

Câu 38:

Trong không gian với hệ tọa độ

O x y z

, cho điểm

M (- 2; 3; - 1)

,

N (- 1; 2; 3)

và

P (2; - 1; 1)

. Phương trình đường thẳng d đi qua M và song song với NP là

A. $\{\begin{cases} x = - 1 + 3 t \\ y = 2 - 3 t \\ z = 3 - 2 t \end{cases}$ .

B.

\{\begin{cases} x = 2 + 3 t \\ y = - 1 - 3 t \\ z = 1 - 2 t \end{cases}

.

C.

\{\begin{cases} x = - 2 + 3 t \\ y = 3 - 3 t \\ z = - 1 - 2 t \end{cases}

.

D.

\{\begin{cases} x = 3 - 2 t \\ y = - 3 + 3 t \\ z = - 2 - t \end{cases}

.

Câu 39:

Cho hàm số f(x). Biết hàm số $f^{'} (x)$ có đồ thị như hình dưới đây. Trên $[- 4; 3]$ , hàm số $g (x) = 2 f (x) + {(1 - x)}^{2}$ đạt giá trị nhỏ nhất tại điểm nào?

Media VietJack

A. $x = - 1$ .

B. x = 3.

C. x = -4.

D. x = -3.

Câu 40:

Xét các số thức

a, b, x, y

thỏa mãn

a > 1, b > 1

và

a^{x} = b^{y} = \sqrt[3]{a b}

. Giá trị nhỏ nhất của biểu thức

Q = x + 3 y

thuộc tập hợp nào dưới đây?

A. $(0; 1)$ .

B.

(2; \frac{5}{2})

(\frac{3}{2}; 2)

.

C.

(\frac{3}{2}; 2)

.

D.

(\frac{5}{2}; 3)

.

Câu 41:

Cho hàm số $f (x)$ có $f (\frac{π}{2}) = \frac{8}{15}$ và $f^{'} (x) = \cos x . \sin^{2} 2 x, \forall \in R$ . Khi đó $\int_{0}^{\frac{π}{2}} f (x) d x$ bằng:

A.

\frac{102}{225}

.

B.

\frac{121}{225}

.

C.

\frac{104}{225}

.

D.

\frac{109}{225}

.

Câu 42:

Cho số phức z thỏa mãn điều kiện

(1 + i) \bar{z} - 1 - 3 i = 0

. Tìm phần ảo của số phức

w = 1 - i z + \bar{z}

.

A. -1

B. i

C. 2

D. -2i

Câu 43:

Cho khối lăng trụ đứng $A B C D . A' B' C' D'$ có đáy là hình thoi cạnh $2 a$ và $B D = 2 a$ (minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng.

Media VietJack

A. $2 \sqrt{3} a^{3}$ .

B.

4 a^{3}

.

C.

6 a^{3}

.

D.

8 \sqrt{3} a^{3}

.

Câu 44:

Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích 200 m³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m². Chi phí thuê công nhân thấp nhất là

A. 36 triệu đồng.

B. 51 triệu đồng.

C. 75 triệu đồng.

D. 46 triệu đồng.

Câu 45:

Trong không gian $O x y z$ , đường thẳng đi qua điểm $M (1; 2; 2)$ , song song với mặt phẳng $(P) : x - y + z + 3 = 0$ đồng thời cắt đường thẳng $d : \frac{x - 1}{1} = \frac{y - 2}{1} = \frac{z - 3}{1}$ có phương trình là

A. $\{\begin{cases} x = 1 - t \\ y = 2 + t \\ z = 2 \end{cases}$

B. $\{\begin{cases} x = 1 + t \\ y = 2 - t \\ z = 2 \end{cases}$

C. $\{\begin{cases} x = 1 - t \\ y = 2 - t \\ z = 2 - t \end{cases}$

D. $\{\begin{cases} x = 1 - t \\ y = 2 - t \\ z = 2 \end{cases}$

Câu 46:

Cho hàm số $y = f (x)$ , hàm số $y = f^{'} (x)$ có đồ thị như hình bên. Hàm số $g (x) = 2 f (\frac{5 \sin x - 1}{2}) + \frac{{(5 \sin x - 1)}^{2}}{4} + 3$ có bao nhiêu điểm cực trị trên khoảng $(0; 2 π)$ .

A. 9

B. 7

C. 6

D. 8

Câu 47:

Tổng tất cả các giá trị của tham số m để phương trình $3^{x^{2} - 2 x + 1 - 2 |x - m|} = \log_{x^{2} - 2 x + 3} (2 |x - m| + 2)$ có đúng ba nghiệm phân biệt là

A. 2

B. 3

C. 1

D. 0

Câu 48:

Cho f(x) là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm M có hoành độ bằng -2 cắt đồ thị tại điểm thứ hai $N (1; 1)$ cắt $O x$ tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là $\frac{9}{16}$ . Tích phân $\int_{- 1}^{1} f (x) d x$ bằng

A. $\frac{31}{18}$ .

B.

\frac{13}{6}

.

C.

\frac{19}{9}

.

D.

\frac{7}{3}

.

Câu 49:

Cho số phức

z = a + b i

(a, b,

\in ℝ

b) thỏa mãn

|z| = 1

. Tìm giá trị lớn nhất của biểu thức

A = |z + 2| + 2 |z - 2|

.

A.

10 \sqrt{2}

.

B. 7.

C. 10.

D.

5 \sqrt{2}

.

Câu 50:

Trong không gian $O x y z$ , cho ba điểm $A (2; - 2; 4)$ , $B (- 3; 3; - 1)$ , $C (- 1; - 1; - 1)$ và mặt phẳng $(P) : 2 x - y + 2 z + 8 = 0$ . Xét điểm M thay đổi thuộc $(P)$ , tìm giá trị nhỏ nhất của biểu thức $T = 2 M A^{2} + M B^{2} - M C^{2}$ .

A. 102.

B. 35.

C. 105.

D. 30.

35 đề minh họa THPT Quốc gia môn Toán năm 2022 có lời giải (Đề 11)

Giới thiệu

Liên kết

Chính sách

Kết nối

35 đề minh họa THPT Quốc gia môn Toán năm 2022 có lời giải (Đề 11)

CHỌN BỘ SÁCH BẠN MUỐN XEM