Bài toán cực trị có tham số đối với một số hàm số cơ bản
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Tìm tất cả các giá trị của m để hàm số có cực đại và cực tiểu.
A.
B.\left[ {\begin{array}{*{20}{c}}{m < 0}\\{m > 1}\end{array}} \right.
C.0<m<1..
D.m<0.
Tìm tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị ?
A.m<0
B.m=0
C.m>0
D.
Cho hàm số . Tất cả các giá trị của m để hàm số có 1 điểm cực trị là:
A.m>−1
B.m<−1
C.m=−1
D.
Tìm tất cả các giá trị của m để hàm số đạt cực đại tại x=2?
A.m=1
B.m=2
C.m=3
D.m=4
Tìm tất cả các giá trị của tham số m để hàm số đạt cực tiểu tại x=1.
A.m=3
B.
C.m=−1
D.m=1
Đồ thị hàm số có điểm cực tiểu và điểm cực đại nằm về hai phía của trục tung khi:
A.1<m<2
B.−2<m<−1
C.2<m<3
D.−3<m<−2
Cho hàm số . Tìm mm để hàm số có các điểm cực đại, cực tiểu thỏa mãn:
A.m=1
B.
C.
D.
Cho hàm số . Tìm m để hàm số có 2 điểm cực trị nhỏ hơn 2
A.m<−2
B.m>4
C.0<m<1
D.−1<m<2
Tìm m để (Cm) : có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân.
A.m=−4
B.m=−1
C.m=1
D.m=3
Cho hàm số . Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác đều là:
A.
B.
C.
D.
Cho hàm số . Tất cả các giá trị của mm để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có diện tích bằng là
A.
B.
C.
D.
Cho hàm số . Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có một góc 120o là:
A.
B.
C.
D.
Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số
A.
B.
C.
D.
Cho hàm số . Tìm mm để đồ thị hàm số có hai điểm cực trị là A,B sao cho đường thẳng AB vuông góc với
A.m=0
B.m=−1
C.m=0;m=2
D.m=1;m=2
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm . Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.
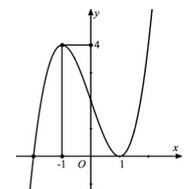
A.−4<m<0
</m<0
B. hoặc
C.m>0 hoặc m<−4
</−4
D.
Cho hàm số với mm là tham số thực. Tìm tất cả các giá trị của m để hàm số có hai điểm cực trị thỏa mãn
A.m>1
B.m<1
C.m>−1
D.m<−1
Cho hàm số với m là tham số thực. Tìm giá trị của mm để đồ thị hàm số có hai điểm cực trị thỏa mãn khoảng cách từ chúng đến trục tung bằng nhau.
A.m=2
B.m=−1
C.m=1
D.m=0
Cho hàm số với m là tham số thực. Tìm giá trị của mm để đồ thị hàm số có hai điểm cực trị A,B sao cho I(1;0) là trung điểm của đoạn thẳng AB.
A.m=0
B.m=−1
C.m=1
D.m=2.
Gọi là giá trị của mm thỏa mãn đồ thị hàm số có hai điểm cực trị A,B sao cho đường thẳng AB đi qua điểm I(1;−3). Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Hàm số (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
A.2
B.3
C.5
D.4
Gọi S là tập hợp tất cả các giá trị thực của tham số mm để đồ thị hàm số có hai điểm cực trị A,B và tam giác OAB vuông tại O. Tổng tất cả các phần tử của S là:
A.9.
B.1.
C.4.
D.5.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
A.3
B.2
C.1
D.4
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị?
A.26.
B.27.
C.16.
D.28.
Cho hàm số . Có bao nhiêu giá trị nguyên của tham số mm để hàm số có đúng 3 điểm cực trị?
A.5
B.3
C.4
D.1