Bất phương trình mũ
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hàm số \[f\left( x \right) = \frac{{{3^x}}}{{{7^{{x^2} - 4}}}}\]. Hỏi khẳng định nào sau đây là sai?
A.\[f\left( x \right) > 9 \Leftrightarrow x - 2 - \left( {{x^2} - 4} \right){\log _3}7 > 0\]
B. \[f\left( x \right) > 9 \Leftrightarrow \left( {x - 2} \right)\ln 3 - \left( {{x^2} - 4} \right)\ln 7 > 0\]
C. \[f\left( x \right) > 9{\rm{\;}} \Leftrightarrow \left( {x - 2} \right)\log 3 - \left( {{x^2} - 4} \right)\log 7 > 0\]
D. \[f\left( x \right) > 9 \Leftrightarrow \left( {x - 2} \right){\log _{0,2}}3 - \left( {{x^2} - 4} \right){\log _{0,2}}7 > 0\]
Tìm tập nghiệm S của bất phương trình \[{5^{x + 1}} - \frac{1}{5} > 0\]
A.\[S = \left( {1; + \infty } \right).\]
B. \[S = \left( { - 1; + \infty } \right).\]
C. \[S = \left( { - 2; + \infty } \right).\]
D. \[S = \left( { - \infty ; - 2} \right).\]
Tìm tập nghiệm của bất phương trình \[{5^x} < 7 - 2x\]
A.R
B.\[\left( { - \infty ;1} \right)\]
c. \[\left( {1; + \infty } \right)\]
D. \[\emptyset \]
Tập hợp nghiệm của bất phương trình: \[{3^{3x - 2}} + \frac{1}{{{{27}^x}}} \le \frac{2}{3}\] là:
A.(2;3)
B.(1;2)
C.{3}
D.\[\left\{ {\frac{1}{3}} \right\}\]
Nghiệm của bất phương trình \[{e^x} + {e^{ - x}} < \frac{5}{2}\] là
A.\[x < - \ln 2\] hoặc\[x > \ln 2\]
B. \[ - \ln 2 < x < \ln 2\]
C.\(x < \frac{1}{2}\) hoặc x>2
D.\(\frac{1}{2} < x < 2\)
Tìm tập nghiệm của bất phương trình \[{7^x} \ge 10 - 3x\]
A.\[\left[ {1; + \infty } \right)\]
B. \[( - \infty ;1]\]
C. \[\left( { - \infty ;\frac{{10}}{3}} \right)\]
D. \[\left( {\frac{{10}}{3}; + \infty } \right)\]
Tìm tập nghiệm của bất phương trình \[{\left( {\frac{1}{2}} \right)^x} \ge 2\].
A.\[\left( { - \infty ; - 1} \right]\]
B. \[\left[ { - 1; + \infty } \right)\]
C. \[\left( { - \infty ; - 1} \right)\]
D. \[\left( { - 1; + \infty } \right)\]
Tìm tập nghiệm S của bất phương trình \[{2^{x - 1}} > {\left( {\frac{1}{{16}}} \right)^{\frac{1}{x}}}\]
A.\[(0, + \infty )\]
B. \[( - \infty , + \infty )\]
C. \[(2, + \infty )\]
D. \[( - \infty ,0)\]
Bất phương trình \[{\left( {\sqrt 2 } \right)^{{x^2} - 2x}} \le {\left( {\sqrt 2 } \right)^3}\]có tập nghiệm là:
A.\[\left[ { - 2;1} \right]\]
B. \[\left( {2;5} \right)\]
C. \[\left[ { - 1;3} \right]\]
D. \[\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\]
Bất phương trình \[{\left( {2 - \sqrt 3 } \right)^x} > {\left( {2 + \sqrt 3 } \right)^{x + 2}}\]có tập nghiệm là:
A.\[\left( { - 1; + \infty } \right)\]
B. \[\left( { - \infty ; - 1} \right)\]
C. \[\left( {2; + \infty } \right)\]
D. \[\left( { - \infty ; - 2} \right)\]
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\frac{1}{3}} \right)^{x - 2}}\]
A.Vô số
B.0
C.9
D.1
Tìm số nghiệm nguyên của bất phương trình \[{\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\]
A.Vô số
B.6
C.4
D.5
Cho hàm số \[f\left( x \right) = {5^x}{.9^{{x^3}}}\], chọn phép biến đổi sai khi giải bất phương trình:
A.\[f\left( x \right) > 1 \Leftrightarrow {\log _9}5 + {x^2} > 0\]
B. \[f\left( x \right) > 1 \Leftrightarrow x.\ln 5 + {x^3}\ln 9 > 0\]
C. \[f\left( x \right) > 1 \Leftrightarrow x{\log _9}5 + {x^3} > 0\]
D. \[f\left( x \right) > 1 \Leftrightarrow x + {x^3}{\log _5}9 > 0\]
Tập nghiệm của bất phương trình \[{\left( {{x^2} + x + 1} \right)^x} < 1\] là:
A.\[\left( {0; + \infty } \right)\]
B. \[\left( { - \infty ;0} \right)\]
C. \[\left( { - \infty ; - 1} \right)\]
D. \[\left( {0;1} \right)\]
Tập nghiệm của bất phương trình \[{3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\] là:
A.\[\left( {0; + \infty } \right)\]
B. \[\left[ {0;2} \right]\]
C. \[\left[ {2; + \infty } \right)\]
D. \[\left[ {2; + \infty } \right) \cup \left\{ 0 \right\}\]
Cho hàm số y=f(x). Hàm số y=f′(x) có bảng biến thiên như sau:
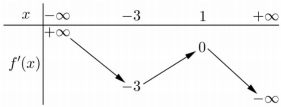
Bất phương trình \[f(x) < {e^x} + m\;\] đúng với mọi \[x \in \left( { - 1;1} \right)\] khi và chỉ khi:
A.\[m \ge f\left( 1 \right) - e\]
B. \[m > f\left( { - 1} \right) - \frac{1}{e}\]
C. \[m \ge f\left( { - 1} \right) - \frac{1}{e}\]
d. \[m > f\left( 1 \right) - e\]
Số nghiệm nguyên của bất phương trình \[{4^x} - {5.2^x} + 4 < 0\]là:
A.1
B.2
C.0
D.3
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \[\left( {{3^{{x^2} - x}} - 9} \right)\left( {{2^{{x^2}}} - m} \right) \le 0\]có 5 nghiệm nguyên?
A.65021
B.65024
C.65022
D.65023
Gọi S là tập hợp các số tự nhiên n có 4 chữ số thỏa mãn \[{\left( {{2^n} + {3^n}} \right)^{2020}} < {\left( {{2^{2020}} + {3^{2020}}} \right)^n}\]. Số phần tử của S là:
A.8999
B.2019
C.1010
D.7979
Cho x;y là hai số thực dương thỏa mãn \[x \ne y\;\] và \[{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\]. Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\]
A.\[\min P = \frac{{13}}{2}.\]
B. \[\min P = \frac{9}{2}.\]
C. \[\min P = - 2.\]
D. \[\min P = 6.\]
Có bao nhiêu giá trị thực của m để bất phương trình \[{4^x} - (m + 1){2^x} + m < 0\;\]vô nghiệm?
A.2
B.vô số
C.1
D.0