Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 18)
Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với Sinx
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Câu 1:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng \(\left( {a;b} \right)\)?
A. 2.
B. \(7\).
C. 4.
D. 3.
Câu 2:
Thể tích \(V\)của khối chóp có diện tích đáy bằng \(S\)và chiều cao bằng \(h\)là
A. \(V = \frac{1}{2}Sh\).
B. \(V = Sh\).
C. \(V = \frac{1}{3}Sh\).
D. \(V = 3Sh\).
Câu 3:
Số đường tiệm cận của đồ thị hàm số \(y = \frac{{2019}}{{x - 3}}\) là
A. \(0\).
B. \(1\).
C. \(2\).
D. \(3\).
Câu 4:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình \(2f\left( x \right) - 5 = 0\) là
A. \(1\).
B. \(0\).
C. \(2\).
D. \(3\).
Câu 5:
Khối bát diện đều là khối đa diện đều loại nào?
A. \(\left\{ {3\,;\,5} \right\}\).
B. \(\left\{ {3\,;\,4} \right\}\).
C. \(\left\{ {4\,;\,3} \right\}\).
D. \(\left\{ {5\,;\,3} \right\}\).
Câu 6:
Cho hình chóp \(S.ABC\)có đáy \(ABC\)là tam giác vuông tại \(B\), \(AB = a\), \(BC = 2a\), \(SA \bot \left( {ABC} \right)\), \(SA = 3a\). Thể tích của khối chóp \(S.ABC\)bằng
A. \(\frac{1}{6}{a^3}\).
B. \(\frac{1}{3}{a^3}\).
C. \(3{a^3}\).
D. \({a^3}\).
Câu 7:
Cho hàm số \(f\left( x \right)\)có đạo hàm \(f'\left( x \right) = - x{\left( {x - 2} \right)^2}\left( {x - 3} \right)\),\(\forall x \in \mathbb{R}\). Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0\,;\,4} \right]\)bằng
A. \(f\left( 4 \right)\).
B. \(f\left( 0 \right)\).
C. \(f\left( 2 \right)\).
D. \(f\left( 3 \right)\).
Câu 8:
Các khoảng đồng biến của hàm số \(y = {x^3} + 3x\) là
A. \(\left( {0;2} \right)\).
B. \(\mathbb{R}\).
C. \(\left( { - \infty ;1} \right)\) và \(\left( {2; + \infty } \right)\).
D. \(\left( {0; + \infty } \right)\).
Câu 9:
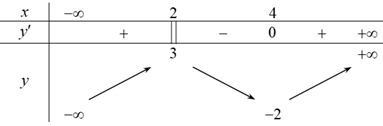
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên \(\left( {2;4} \right)\).
B. Hàm số nghịch biến trên \(\left( {4; + \infty } \right)\).
C. Hàm số đồng biến trên \(\left( { - \infty ;3} \right)\).
D. Hàm số đồng biến trên \(\left( { - 2; + \infty } \right)\).
Câu 10:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
Gọi \(S\) là tập hợp các giá trị cực đại của hàm số. Kết quả nào sau đây đúng?
A. \(S = \left\{ { - 1;\;1;\;3;\;5} \right\}\).
B. \(S = \left\{ {3;\;5} \right\}\).
C. \(S = \left\{ {2;\;3;\;5} \right\}\).
D. \(S = \left\{ 5 \right\}\).
Câu 11:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Tìm khẳng định đúng.
A. Hàm số đạt cực đại tại \(x = 1\) và đạt cực tiểu \(x = 2\).
B. Hàm số có giá trị cực tiểu bằng \(1\).
C. Hàm số có giá trị lớn nhất bằng \(1\) và giá trị nhỏ nhất bằng \(0\).
D. Hàm số có đúng một cực trị.
Câu 12:
Hàm số nào trong các hàm số sau đây có đồ thị như hình vẽ?
A. \(y = - {x^4} + 2{x^2}\).
B. \(y = {x^4} - 2{x^2} - 1\).
C. \(y = {x^4} - 2{x^2} + x\).
D. \(y = {x^4} - 2{x^2}\).
Câu 13:
Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3x\)trên đoạn \[{\rm{[}} - 3;3]\]bằng
A. \( - 2\).
B. \(2\).
C. \( - 18\).
D. \(18\).
Câu 14:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. \(4.\)
B. \(3.\)
C. \(1.\)
D. \(2.\)
Câu 15:
Hình lăng trụ tam giác có bao nhiêu cạnh?
A. \[9\].
B. \[12\].
C. \[6\].
D. \[10\].
Câu 16:
Cho khối lăng trụ có đáy hình vuông cạnh \(a\sqrt 2 \) chiều cao bằng \[4a\]. Tính thể tích khối lăng trụ đã cho.
A. \(4{a^3}\).
B. \(16{a^3}\).
C. \(8{a^3}\).
D. \(\frac{{16{a^3}}}{3}\)
Câu 17:
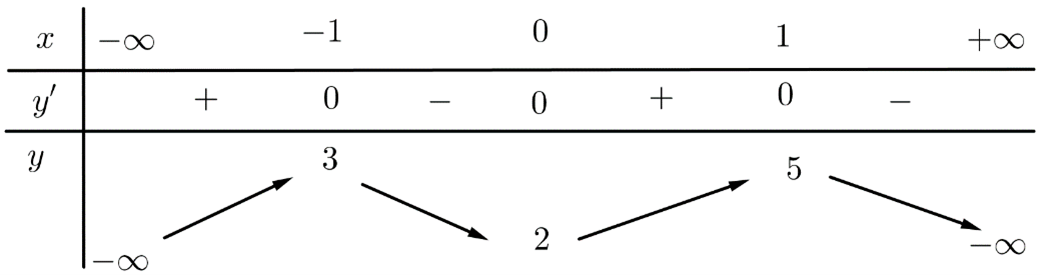
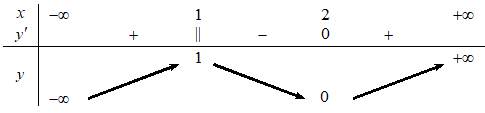
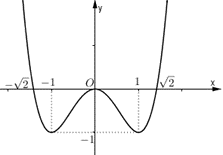
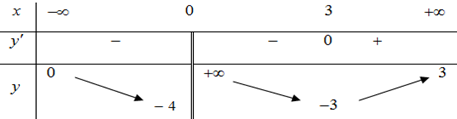
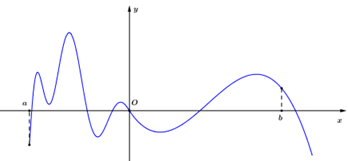
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có đồ thị như sau
Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng nào dưới đây?
A. \(\left( {0; + \infty } \right)\).
B. \(\left( { - \infty ; - 1} \right)\).
C. \(\left( { - 1;1} \right)\).
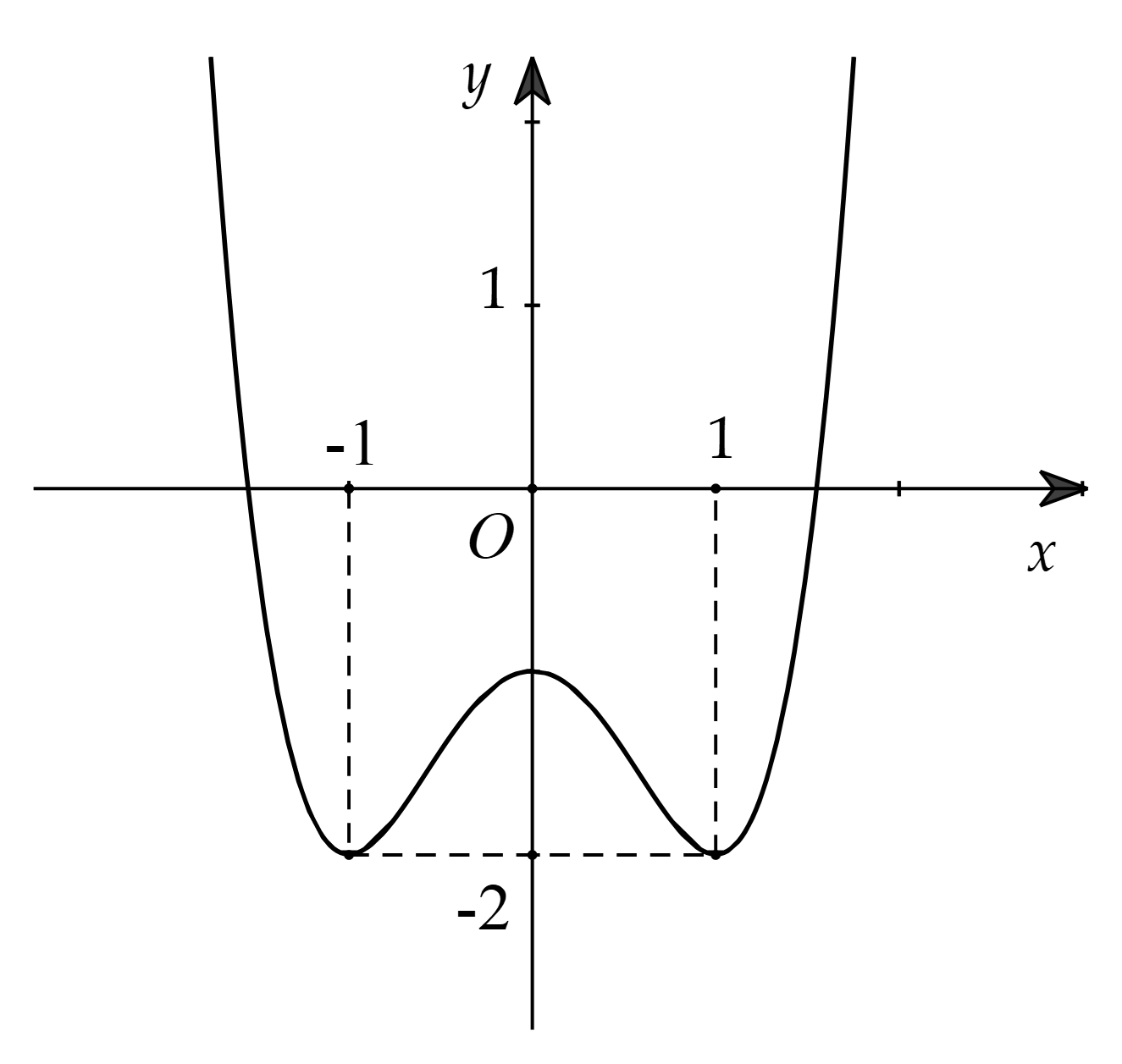
D. \(\left( { - \infty ;0} \right)\).
Câu 18:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y = \frac{{5x - 3}}{{{x^2} - 2mx + 1}}\) không có tiệm cận đứng.
A. \(m = 1\).
B. \(\left[ \begin{array}{l}m > 1\\m < - 1\end{array} \right.\).
C. \( - 1 < m < 1\).
D. \(m = - 1\).
Câu 19:
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\), có đạo hàm \[f'\left( x \right) = {\left( {x - 2} \right)^4} + 1\]. Khẳng định nào sau đây đúng?
A. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( { - \infty ;2} \right)\] và nghịch biến trên khoảng \[\left( {2; + \infty } \right)\].
B. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( {2; + \infty } \right)\] và nghịch biến trên khoảng \[\left( { - \infty ;2} \right)\].
C. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\].
D. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - \infty ; + \infty } \right)\].
Câu 20:
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có bảng biến thiên như sau:
Tính \(S = a + b.\)
A. \(S = - 1.\)
B. \[S = - 2.\]
C. \[S = 1.\]
D. \[S = 0.\]
Câu 21:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy \(\left( {ABC} \right)\). Biết góc tạo bởi \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích \(V\) của khối chóp \(SABC\).
A. \(V = \frac{{{a^3}\sqrt 3 }}{8}\).
B. \(V = \frac{{{a^3}\sqrt 3 }}{{12}}\).
C. \(V = \frac{{{a^3}\sqrt 3 }}{{24}}\).
D. \(V = \frac{{3\sqrt 3 {a^3}}}{8}\).
Câu 22:
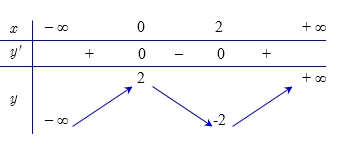
Khối lập phương \(ABCD.A'B'C'D'\)có cạnh bằng \(a.\) Khi đó thể tích khối chóp \(D.ABC'D'\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{3}\).
B. \(\frac{{{a^3}}}{3}\).
C. \(\frac{{{a^3}}}{4}\).
D. \(\frac{{{a^3}\sqrt 2 }}{6}\).
Câu 23:
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \), cạnh \(AB = 2a\). Thể tích \(V\) của khối lăng trụ \(ABC.A'B'C'\) bằng
A. \(2{a^3}\).
B. \(3{a^3}\sqrt 3 \).
C. \({a^3}\sqrt 3 \).
D. \(6{a^3}\).
Câu 24:
Tìm tất cả giá trị thực của tham số \[m\]để hàm số \[y = \left( {m - 1} \right){x^4} - 2\left( {m - 3} \right){x^2} + 1\] không có cực đại.
A. \(m \le 1\).
B. \(1 < m \le 3\).
C. \(m \ge 1\).
D. \(1 \le m \le 3\).
Câu 25:
Tìm tất cả giá trị của tham số \[m\]để hàm số \[f\left( x \right) = {x^3} + 3{x^2} + {m^2} - 5\]có giá trị lớn nhất trên đoạn \[\left[ { - 1;2} \right]\]là 19.
A. \[m = 2\]và \[m = 3\].
B. \[m = 1\]và \[m = - 2\].
C. \[m = 2\]và \[m = - 2\].
D. \[m = 1\]và \[m = 3\].
Câu 26:
Biết đồ thị hàm số \(y = f\left( x \right)\) có một tiệm cận ngang là \(y = 3\). Khi đó đồ thị hàm số \(y = 2f\left( x \right) - 4\) có một tiệm cận ngang là
A. \(y = 3\).
B. \(y = 2\).
C. \(y = 1\).
D. \(y = - 4\).
Câu 27:
Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = - \frac{1}{3}{x^3} - m{x^2} + \left( {2m - 3} \right)x + 2018\)nghịch biến trên \(\mathbb{R}\).
A. \( - 3 \le m \le 1\).
B. \( - 3 < m < 1\).
C. \(m \ge 1\)hoặc \(m \le - 3\).
D. \(m \le 1\).
Câu 28:
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ:
Khi đó phương trình \(2f\left( x \right) - 1 = 0\) có bao nhiêu nghiệm thực phân biệt.
A. 3.
B. 0.
C. 1.
D. 2.
Câu 29:
Cho hàm số \(y = \sqrt {{x^2} - 2x - 3} \). Khẳng định nào sau đây là đúng?
A. \({\rm{max}}y = 1\).
B. \({\rm{max}}y = 2\).
C. \({\rm{max}}y = 0\).
D. Hàm số không có giá trị lớn nhất.
Câu 30:
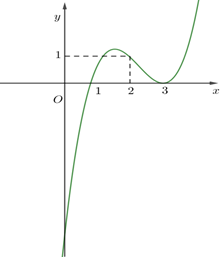
Đường cong ở hình vẽ dưới đây là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực.
Mệnh đề nào dưới đây đúng ?
A. \(y' < 0,\forall x \ne - 1.\)
B. \(y' > 0,\forall x \in \mathbb{R}.\)
C. \(y' > 0,\forall x \ne 2.\)
D. \(y' > 0,\forall x \ne - 1.\)
Câu 31:
Số điểm cực trị của hàm số \(f\left( x \right)\)có đạo hàm \(f'\left( x \right) = \left( {x + 1} \right){\left( {x - 2} \right)^2},\forall x \in \mathbb{R}\) là
A. \(0\).
B. \(3\).
C. \(1\).
D. \(2\).
Câu 32:
Cho hình chóp \(S.ABC\)có đáy \(ABC\)là tam giác vuông cân tại \(B\), \(SA\)vuông góc với mặt đáy\(\left( {ABC} \right),\;BC = a\), góc hợp bởi \(\left( {SBC} \right)\)và \(\left( {ABC} \right)\)là \({60^ \circ }\). Mặt phẳng \(\left( P \right)\)qua \(A\)vuông góc với \(SC\)cắt \(SB,SC\)lần lượt tại \(D,E\). Thể tích khối đa diện \(ABCED\)là
A. \(\frac{{3\sqrt 3 {a^3}}}{{40}}\).
B. \(\frac{{\sqrt 3 {a^3}}}{6}\).
C. \(\frac{{11\sqrt 3 {a^3}}}{{120}}\).
D. \(\frac{{3\sqrt 3 {a^3}}}{{60}}\).
Câu 33:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đúng hai điểm cực trị \(x = - 1,x = 1,\) có đồ thị như hình vẽ sau:
Hỏi hàm số \(y = f\left( {{x^2} - 2x + 1} \right) + 2020\) có bao nhiêu điểm cực tiểu?
A. \(4\).
B. \(3\).
C. \(2\).
D. \(1\).
Câu 34:
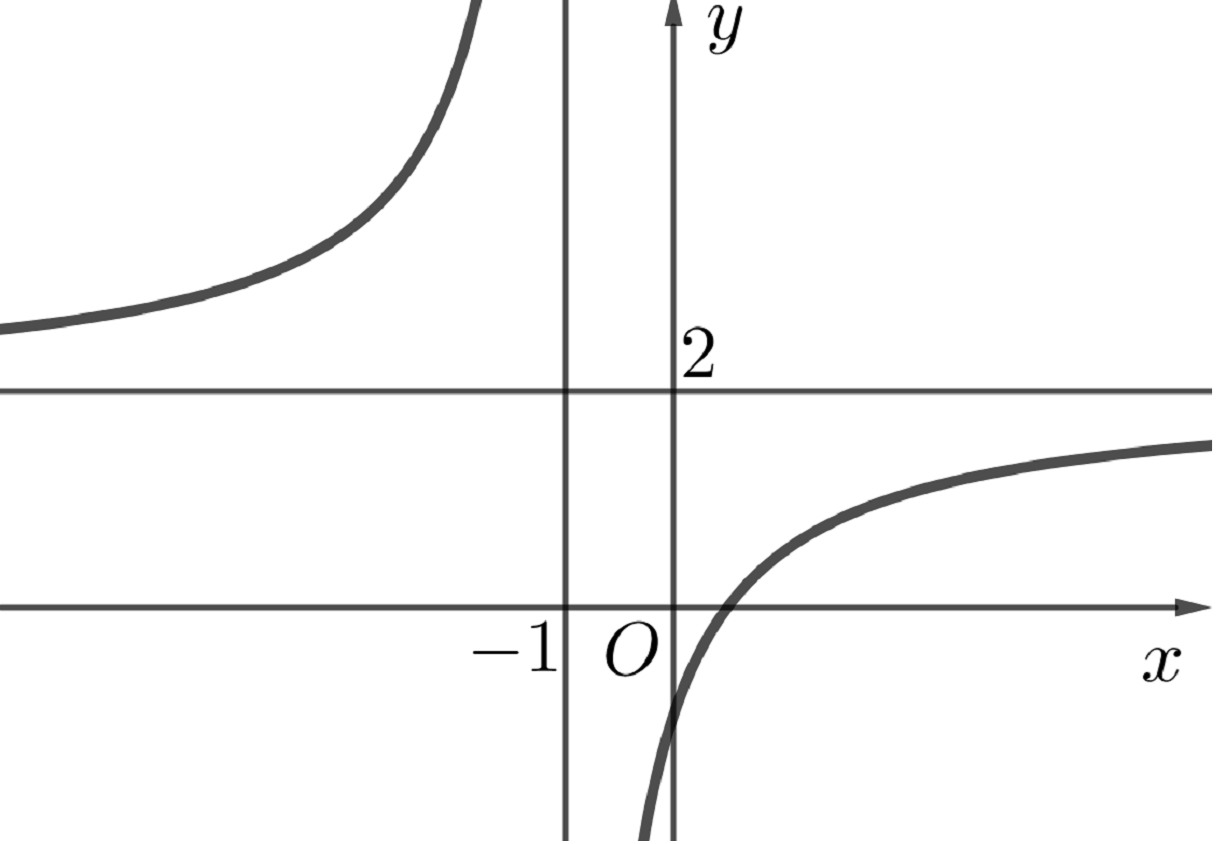
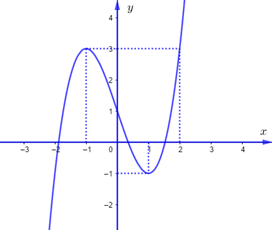
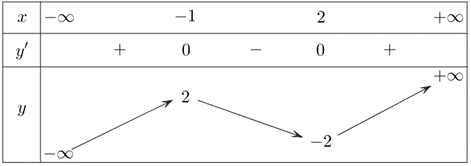
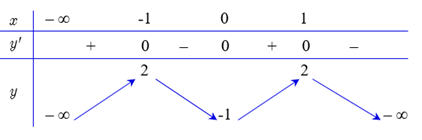
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Số nghiệm thuộc \(\left[ {0;\frac{{3\pi }}{2}} \right]\) của phương trình \(\left| {f\left( {\cos 2x} \right)} \right| = 1\) là
A. \(9\).
B. \(4\).
C. \(7\).
D. \(10\).
Câu 35:
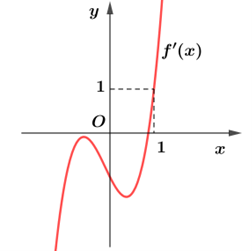
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình bên.
Hàm số \(g\left( x \right) = f\left( {{x^2} + 2x} \right) - {x^2} - 2x\)đồng biến trên khoảng nào dưới đây?
A. \(\left( { - 1 - \sqrt 2 ; - 1} \right)\).
B. \(\left( { - 1 - \sqrt 2 ; - 1 + \sqrt 2 } \right)\).
C. \(\left( { - 1; + \infty } \right)\).
D. \(\left( { - 1; - 1 + \sqrt 2 } \right)\).