Bộ đề thi thử Đại học môn Toán mới nhất cực hay có lời giải (Đề 2)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
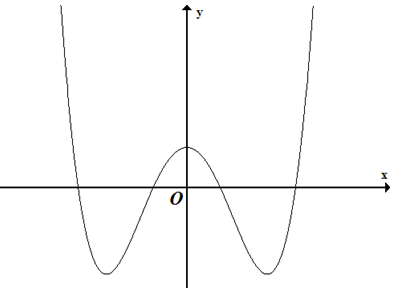
A. y = x4 + 5x2 + 2
B. y = x3 – 3x2 + 2
C. y = x4 – 5x2 + 2
D. y = x4 + 5x2 + 2
Tìm giá trị lớn nhất M của hàm số y = x3 – 3x2 trên đoạn [-1; 1].
A. M = 4
B. M = -2
C. M = 0
D. M = 2
Khối lăng trụ có diện tích đáy bằng 24 cm2, chiều cao bằng 3 cm thì có thể tích bằng
A. 24 (cm3)
B. 72 (cm3)
C. 8 (cm3)
D. 126(cm3)
Hàm số nghịch biến trên các khoảng:
A. R \ {1}
B. (-∞; 1) và (1; +∞)
C. (-∞; 2) và (2; +∞)
D. (-∞; -5) và (-5; +∞)
Khối lăng trụ ngũ giác có bao nhiêu mặt?
A. 7 mặt
B. 9 mặt
C. 6 mặt
D. 5 mặt
Đồ thị sau đây là của hàm số nào?
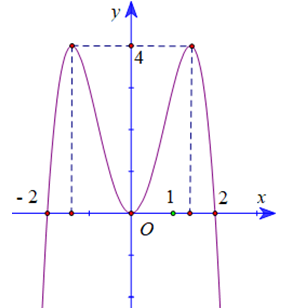
Hàm số có bao nhiêu điểm cực trị.
A. 3
B. 1
C. 0
D. 2
Tìm phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
A. x = 1, y = 2
B. x = 2, y = -2
C. x = -2, y = 2
D. x = 2, y = 1
Cho hàm số . Tọa độ điểm cực tiểu của đồ thị hàm số là
B. (1; -2)
C. (1; 2)
D. (-1; 2)
Cho hàm số y = f(x) có bảng biến thiên như sau
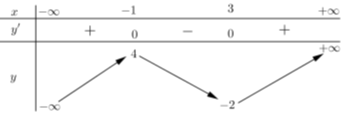
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
A. (-∞; -1)
B. (-1; 3)
C. (-2; 4)
D. (3; +∞)
Trong một hình đa diện, mệnh đề nào dưới đây đúng?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
B. Hai mặt bất kỳ có ít nhất một cạnh chung.
C. Hai cạnh bất kỳ có ít nhất một điểm chung.
D. Hai mặt bất kỳ có ít nhất một điểm chung.
Cho hàm số có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị (C) với trục tung là
A. y = x – 2
B. y = –x + 2
C. y = –x + 1
D. y = –x –2
Cho khối lăng trụ ABC.A’B’C’ có thể tích là V. Thể tích của khối tứ diện C A’B’C’ bằng
Cho hình lăng trụ đứng ABC.A’B’C’ có tam giác ABC vuông tại A, AB = AA’ = a, AC = 2a. Tính thể tích khối lăng trụ đã cho.
B. a3
C. 2a3
Thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ có AB = AD = 2, AA’ = 3 là
A. 12
B. 2
C. 4
D. 6
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
A. Một
B. Hai
C. Bốn
D. Ba
Cho hàm số y = -x4 + 6x2 + 1 có đồ thị (C). Mệnh đề nào dưới đây đúng?
Cho hàm số có đồ thị (C). Số giá trị nguyên của tham số m để có ba tiếp tuyến của(C) song song với đường thẳng d: y = mx là
A. 26
B. 28
C. 27
D. 25
Số giao điểm của đường cong y = x3 – 2x2 + 2x + 1 và đường thẳng y = 1 - x là
A. 1
B. 3
C. 0
D. 2
Với a, b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x3 + ax2 – bx + 1 là
A. 2
B. 1
C. 0
D. 3
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
A. 3
C. 2
Khối hộp chữ nhật ABCD.A’B’C’D’ có độ dài AD, AD’, AC’ lần lượt là 1; 2; 3. Tính thể tích V của khối chóp A.A’B’C’D’.
Nếu ba kích thước của một khối hộp chữ nhật tăng lên 3 lần thì thể tích của nó tăng lên bao nhiêu lần?
A. 3 lần
B. 9 lần
C. 18 lần
D. 27 lần
Cho hàm số y = f(x) xác định và có đạo hàm trên R \ { ± 1}. Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?
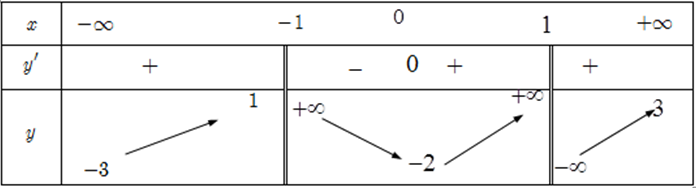
A. 3
B. 2
C. 4
D. 1
Hàm số y = x4 – 2x2 đồng biến trên khoảng nào sau đây?
A. (-∞; 0)
B. (-1; 1)
C. (-1; 0)
D. (0; +∞)
Cho lăng trụ tam giác đều ABC.A’B’C’ có chiều cao bằng 3. Biết hai đường thẳng AB’, BC’ vuông góc với nhau. Tính thể tích của khối lăng trụ.
Tìm giá trị nhỏ nhất của hàm số
B. 1
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD = 2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD.
Đồ thị hàm số y = ax3 + bx2 + cx + d (a, b, c, d là các hằng số thực và a ≠ 0) như hình vẽ.
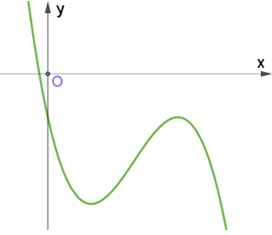
Khẳng định nào đúng
A. b > 0, c > 0
B. b < 0, c < 0
C. b < 0, c > 0
D. b > 0, c < 0
Cho hàm số f(x) = ax4 + bx2 + c (a ≠ 0) có đồ thị hàm số như hình vẽ:
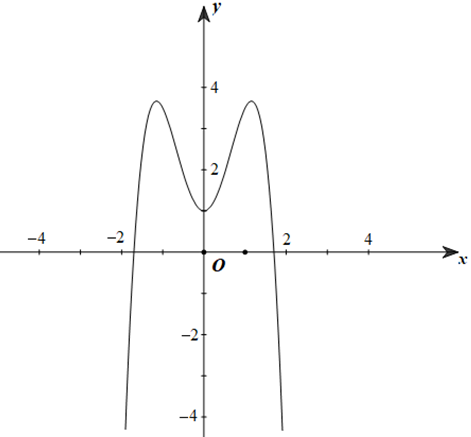
Tìm mệnh đề đúng trong các mệnh đề sau:
A. a > 0; b < 0; c > 0
B. a < 0; b > 0; c < 0
C. a < 0; b < 0; c > 0
D. a < 0; b > 0; c > 0
Tìm tất cả tham số thực m để hàm số có cực đại, cực tiểu.
A. m ∈ (-3; 1)
B. m ∈ (-∞; -3) ∪ (1; +∞)
C. m ∈ (-3; -2) ∪ (-2; 1)
D. m ∈ (-2; 1)
Cho hàm số f(x) = |3x4 – 4x3 – 12x2 + m|. Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1; 3] Giá trị nhỏ nhất của M bằng
C. 16
Cho hàm số y = f(x) liên tục trên đoạn [-2; 2] và có đồ thị là đường cong như hình vẽ bên. Tìm số nghiệm của phương trình |f(x)| = 1 trên đoạn [-2; 2].
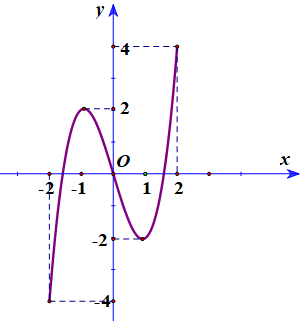
A. 3
B. 5
C. 6
D. 4
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
Cho hàm số y = f(x) có đạo hàm liên tục trên R, thỏa mãn 2f(2x) + f(1 – 2x) = 12x2. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1 là
A. y = 4x - 6
B. y = 2x - 6
C. y = 4x - 2
D. y = 2x + 2
Có bao nhiêu số nguyên dương m để hàm số nghịch biến trên khoảng (3; 6)?
A. 6
B. 4
C. 7
D. 3
Cho số thực a và hàm số . Số tiệm cận nhiều nhất ( nếu có ) của đồ thị hàm số trên là
A. 3
B. 1
C. 2
D. 0
Hàm số đạt cực đại tại x = 2 khi giá trị của m bằng
A. -3
B. 3
C. -1
D. 1
Cho hàm số y = f(x). Hàm số y = f’(x) có đồ thị như hình bên. Hàm số y = f(x2) có bao nhiêu điểm cực trị?
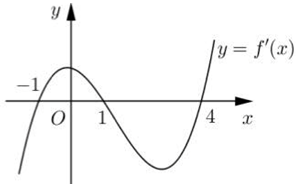
A. 3
B. 1
C. 5
D. 2
Biết đồ thị (C) của hàm số luôn cắt đường thẳng (d): y = -x + m tại hai điểm phân biệt A, B.Tìm giá trị của tham số m để độ dài đoạn AB là ngắn nhất.
B. m = 1
C. m = 0
D. m = 4
Cho hàm số y = f(x) = ax4 + bx2 + c biết a > 0, c > 2017 và a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 3
C. 7
D. 5
Cho hai tam giác đều ABC và ABD có độ dài cạnh bằng 1 và nằm trong hai mặt phẳng vuông góc. Gọi S là điểm đối xứng của B qua đường thẳng DC. Tính thể tích của khối đa diện ABDSC.
Một người thợ nhôm kính nhận đơn đặt hàng làm một bể cá cảnh bằng kính dạng hình hộp chữ nhật không có nắp có thể tích 3,2 m3; tỉ số giữa chiều cao của bể cá và chiều rộng của đáy bằng 2 (hình dưới). Biết giá một mét vuông kính để làm thành và đáy bể cá là 800 nghìn đồng. Hỏi người thợ đó cần tối thiểu bao nhiêu tiền để mua đủ số mét vuông kính làm bể cá theo yêu cầu (coi độ dày của kính là không đáng kể so với kích thước của bể cá).
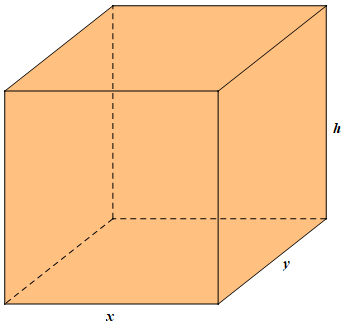
A. 9,6 triệu đồng
B. 10,8 triệu đồng
C. 8,4 triệu đồng
D. 7,2 triệu đồng
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số 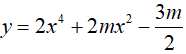 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
B. -3
C. -1
D. 0
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |3x4 – 4x3 – 12x2 + m| có 5 điểm cực trị.
A. 27
B. 16
C. 26
D. 44
Tất cả giá trị nào của m thì hàm số y = x(m – x2) + m nghịch biến trên khoảng (-1; 1)
A. m < 0
B. m < 3
C. m ≤ 3
D. m ≤ 0
Một Bác nông dân cần xây dựng một hố ga không nắp dạng hình hộp chữ nhật có thể tích 3200 cm3, tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng 2. Hãy xác định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất?
A. 1200 cm2
B. 1600 cm2
C. 160 cm2
D. 120 cm2
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, mặt bên tạo với đáy góc 75o. Mặt phẳng (P) chứa đường thẳng AB và tạo với đáy góc 45o chia khối chóp S.ABCD thành hai khối đa diện. Thể tích của khối đa diện chứa đỉnh S bằng
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x3 – 3x2 tại 3 điểm phân biệt A, B, C (B nằm giữa A và C) sao cho AB = 2BC. Tính tổng các phần tử thuộc S.
B. 0
C. -2
D. -4
Một trong các đồ thị dưới đây là đồ thị của hàm số g(x) liên tục trên R thỏa mãn g’(0) = 0, g’’(x) < 0 ∀x ∈ (-1; 2). Hỏi đồ thị của hàm số g(x) là đồ thị nào?