Các dạng toán viết phương trình mặt phẳng
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Trong không gian Oxyz, cho mặt phẳng . Vec-tơ nào sau đây không là vecto pháp tuyến của mặt phẳng (P) .
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận làm vectơ pháp tuyến.
A.
B.
C.
D.
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng là:
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2), B(2,−3,−2). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
A.
B.
C.
D.
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1) . Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
A.
b.
C.
D.
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với và .
A.
B.
C.
D.
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng và . Tính khoảng cách giữa (P) và (Q).
A.9
B.6
C.5
D.3
Viết phương trình mặt phẳng (P) song song với mặt phẳng và cách (Q) một khoảng là .
A. hoặc .
B. hoặc
C. hoặc .
D. hoặc .
Trong không gian Oxyz, cho hai mặt phẳng Hai mặt phẳng (P và (Q) song song với nhau khi m bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng và . Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.
A.m=−2
B.m=3
C.m=−3
D.m=2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng qua hai điểm A(3,2,1),B(−3,5,2) và vuông góc với mặt phẳng . Tính tổng
A.S=−2
B.S=2
C.S=−4
D.S=−12
Trong hệ trục toạ độ không gian Oxyz, cho biết b,c>0, phương trình mặt phẳng . Tính biết
A.2
B.
C.
D. 1
Cho mặt phẳng (P) có phương trình và mặt phẳng (Q) có phương trình . Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
A.Mặt phẳng (Oxy)
B.Mặt phẳng (Oyz)
C.Mặt phẳng (Oxz)
D.Mặt phẳng (Q)
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho. Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình .
B.(S) là mặt phẳng có phương trình .
C.(S) là mặt phẳng có phương trình .
D.(S) là mặt phẳng có phương trình .
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình và . Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình x=0.
B.(S) là mặt phẳng có phương trình .
C.(S) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x=0 và
D.(S) là hai mặt phẳng có phương trình x=0x=0 và
Với mỗi giá trị của tham số m, xét mặt phẳng (Pm) xác định bởi phương trình . Tìm tọa độ của điểm thuộc mọi mặt phẳng (Pm).
A. (1,−2,1)
B.(0,1,1)
C.(3,−1,1)
D.Không có điểm như vậy.
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng và là:
A.
B.
C.
D.
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x′Ox,y′Oy,z′Oz lần lượt tại các điểm A,B,C sao cho ?
A.3.
B.1.
C.4.
D.8.
Cho mặt phẳng đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng
A.1
B.
C.
D. 2
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:
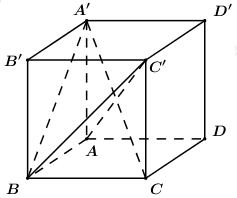
A.
B.
C. 0
D.
Trong không gian Oxyz, hai mặt phẳng và chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
A.
B.
C.
D.
Trong không gian Oxyz, cho ba mặt phẳng và . Tính tổng , biết và
A. -6
B. 1
C. 0
D. 6