Cách xét tính đồng biến, nghịch biến của hàm số

  • 1Làm xong biết đáp án, phương pháp giải chi tiết.
  • 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
  • 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
  • 4Biết điểm yếu và có hướng giải pháp cải thiện

Số câu đúng

0/11

Thời gian làm bài

00:00:00

Số câu đã làm

0

Câu 1:
Cho hàm số​​ f(x) = 4 – 3x. Khẳng định nào sau đây đúng?
A.​​ Hàm số​​ đồng biến​​ trên​​ (–∞; 43);
B.​​ Hàm số​​ nghịch biến trên​​ (43; +∞);​​
C.​​ Hàm số​​ đồng biến trên​​ ℝ;
D.​​ Hàm số​​ đồng biến trên​​ (34; +∞).
Câu 2:
Xét tính đồng biến, nghịch biến của hàm số​​ f(x) = 4x + 5​​ trên khoảng​​ (–∞; 2)​​ và trên khoảng​​ (2; +∞). Khẳng định nào sau đây đúng ?
A.​​ Hàm số​​ nghịch biến trên​​ (–∞; 2),​​ đồng biến trên​​ (2; +∞);
B.​​ Hàm số​​ đồng biến trên​​ (–∞; 2),​​​​ nghịch biến trên​​ (2; +∞);
C.​​ Hàm số​​ nghịch biến trên các khoảng​​ ​​(–∞; 2) và​​ (2; +∞);
D.​​ Hàm số​​ đồng biến trên các khoảng​​ ​​(–∞; 2) và​​ (2; +∞).
Câu 3:
Xét sự​​ biến thiên của hàm số​​ f(x) = 3x​​ trên khoảng​​ (0; +∞). Khẳng định nào sau đây đúng ?
A.​​ Hàm số​​ đồng biến trên khoảng​​ (0; +∞);
B.​​ Hàm số​​ nghịch biến trên khoảng​​ (0; +∞);
C.​​ Hàm số​​ vừa đồng biến, vừa nghịch biến trên khoảng​​ (0; +∞);
D.​​ Hàm số​​ không đồng biến, cũng không nghịch biến trên khoảng​​ (0; +∞).
Câu 4:
Xét tính đồng biến, nghịch biến của hàm số y = –0,5x. Khẳng định nào sau đây là sai:
A. Hàm số đồng biến trên khoảng (0; 10);
B. Hàm số nghịch biến trên khoảng (–1; 5);
C. Hàm số nghịch biến trên khoảng (–5; –2022);
D. Hàm số nghịch biến trên khoảng (100; 10000).
Câu 5:
Xét tính đồng biến, nghịch biến của hàm số y = –0,5x. Khẳng định nào sau đây là sai:
A. Hàm số đồng biến trên khoảng (0; 10);
B. Hàm số nghịch biến trên khoảng (–1; 5);
C. Hàm số nghịch biến trên khoảng (–5; –2022);
D. Hàm số nghịch biến trên khoảng (100; 10000).
Câu 6:

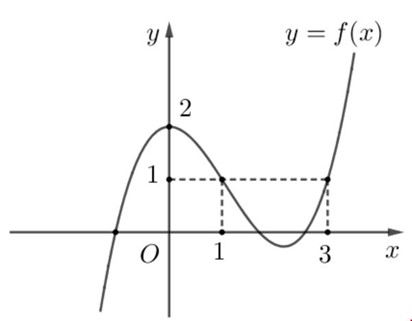
Cho hàm số có đồ thị như hình dưới:

Media VietJack

Khẳng định nào dưới đây là đúng ?

A. Hàm số đồng biến trên khoảng (0; 1);
B. Hàm số đồng biến trên khoảng (1; 3);
C. Hàm số nghịch biến trên khoảng (0; 1);

D. Hàm số nghịch biến trên khoảng (3; +∞).

Câu 7:

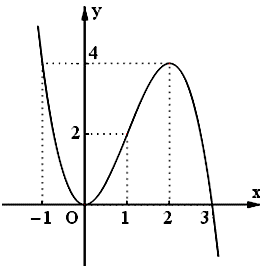
Cho hàm số có đồ thị như hình dưới:

Media VietJack

Khẳng định nào dưới đây là sai ?

A. Hàm số đồng biến trên khoảng (0; 1);
B. Hàm số đồng biến trên khoảng (2; 3);
C. Hàm số nghịch biến trên khoảng (–1; 0);
D. Hàm số nghịch biến trên khoảng (3; +∞).
Câu 8:

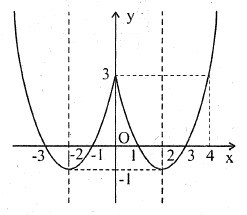
Cho hàm số có đồ thị như hình dưới:

Media VietJack

Khẳng định nào dưới đây là đúng ?

A. Hàm số đồng biến trên khoảng (0; 1);
B. Hàm số đồng biến trên khoảng (2; 4);
C. Hàm số nghịch biến trên khoảng (–2; 0);
D. Hàm số nghịch biến trên khoảng (3; +∞).
Câu 9:
Trong các hàm số sau, hàm số nào đồng biến trên khoảng (–1; 0) ?
A. y = x;
B. y=1xy = \frac{1}{x};
C. y = |x|;
D. y = x2.
Câu 10:
Cho hàm số y = 2x2. Khẳng định nào sau đây là đúng ?
A. Hàm số trên đồng biến trên khoảng (0; +∞);
B. Hàm số trên nghịch biến trên khoảng (0; +∞);
C. Hàm số trên đồng biến trên ℝ;
D. Hàm số trên nghịch biến trên ℝ.
Câu 11:
Cho hàm số f(x)=4x+1f(x) = \frac{4}{{x + 1}}. Khẳng định nào sau đây là đúng ?
A. f(x) đồng biến trên khoảng (–∞; –1) và nghịch biến trên khoảng (–1; +∞);
B. f(x) đồng biến trên các khoảng (–∞; –1) và (–1; +∞);
C. f(x) nghịch biến trên khoảng (–∞; –1) và đồng biến trên khoảng (–1; +∞);
D. f(x) nghịch biến trên các khoảng (–∞; –1) và (–1; +∞).