Chia đơn thức cho đơn thức

  • 1Làm xong biết đáp án, phương pháp giải chi tiết.
  • 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
  • 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
  • 4Biết điểm yếu và có hướng giải pháp cải thiện

Số câu đúng

0/10

Thời gian làm bài

00:00:00

Số câu đã làm

0

Câu 1:

Kết quả của phép chia 15x3y4 : 5x2y2 là

A. 3xy2;      

B. –3x2y;    

C. 5xy;        

D. 15xy2.

Câu 2:

Chia đơn thức (–3x)5 cho đơn thức (–3x)2 ta được kết quả là

A. –9x3;       

B. 9x3;         

C. 27x3;       

D. –27x3.

Câu 3:

Thương của phép chia (–xy)6 : (2xy)4 bằng

A. (–xy)2;     

B. (xy)2;      

C. (2xy)2;    

D. .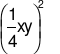 

Câu 4:

Chọn câu đúng.

A. 20x5y3 : 4x2y2 = 5x3y2;          

B. ;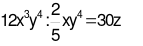 

C. ;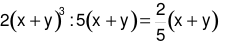 

D. x2yz3 : (–x2z3) = –y.

Câu 5:

Cho hai biểu thức ; . Khi đó A : B bằng

A. 16x4y6;    

B. 8x3y8;     

C. 4x3y7;      

D. 16x3y7.

Câu 6:

Chọn câu đúng.

A. 24x4y3 : 12x3y3 = 2xy;          

B. 18x6y5 : (–9x3y3) = 2x3y2;

C. 40x5y2 : (–2x4y2) = –20x;       

D. 9a3b4x4 : 3a2b2x2 = 3ab3x2.

Câu 7:

Giá trị số tự nhiên n để phép chia x2n : x4 thực hiện được là:

A. n ∈ ℕ, n > 2; 

B. n ∈ ℕ, n ≥ 4; 

C. n ∈ ℕ, n ≥ 2; 

D. n ∈ ℕ, n ≤ 2.

Câu 8:

Cho hai đơn thức: B = 4x4y4 ; C = xn – 1y4. Điều kiện của số tự nhiên n (n > 0) để đơn thức B chia hết đơn thức C là

A. n = 5;       

B. 0 < n ≤ 5; 

C. n ≥ 5;       

D. n = 0.

Câu 9:

Cho hai biểu thức 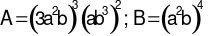. Khi đó A : B bằng

A. 27ab5;     

B. –27b5;     

C. 27b5;       

D. 9b5.

Câu 10:

Giá trị số tự nhiên n để phép chia xn : x6 thực hiện được là

A. n ∈ N, n < 6; 

B. n ∈ N, n ≥ 6; 

C. n ∈ N, n > 6; 

D. n ∈ N, n ≤ 6.