Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 2: Phép tịnh tiến

Phép dời hình nào có thể biến hình ngôi sao A thành hình ngôi sao B?

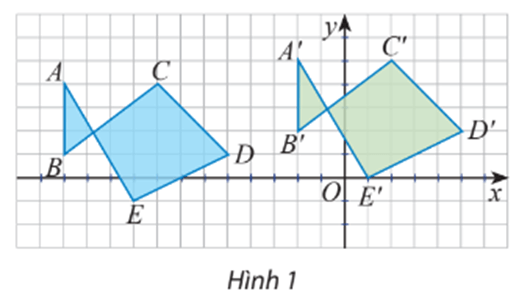
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).

a) Có nhận xét gì về các vectơ $\overrightarrow{{\mathrm{AA}}^{\text{'}}},\mathrm{\hspace{0.17em}}\overrightarrow{{\mathrm{BB}}^{\text{'}}},\mathrm{\hspace{0.17em}}...,\mathrm{\hspace{0.17em}}\overrightarrow{{\mathrm{EE}}^{\text{'}}}$

b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?

Chứng minh phép đồng nhất là một phép tịnh tiến.

Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ $\overrightarrow{\mathrm{v}}$ biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).

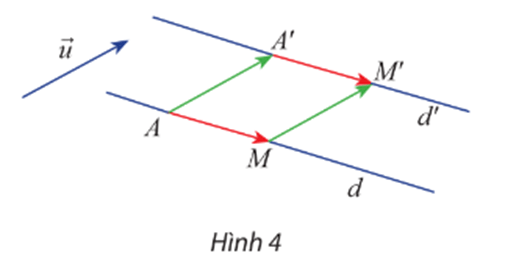
Cho vectơ $\overrightarrow{\mathrm{u}}$ và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến ${\mathrm{T}}_{\overrightarrow{\mathrm{u}}}$.

a) Hai vectơ $\overrightarrow{{\mathrm{A}}^{\text{'}}{\mathrm{M}}^{\text{'}}},\mathrm{\hspace{0.17em}\hspace{0.17em}}\overrightarrow{\mathrm{AM}}$ có bằng nhau không?

b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.

Trong mặt phẳng tọa độ Oxy, xét phép tịnh tiến ${\mathrm{T}}_{\overrightarrow{\mathrm{v}}}$ với $\overrightarrow{\mathrm{v}}=\left(3;2\right)$.

a) Biết ảnh của điểm M qua ${\mathrm{T}}_{\overrightarrow{\mathrm{v}}}$ là điểm M’(–8; 5). Tìm tọa độ điểm M.

b) Tìm ảnh của đường tròn (C): (x – 2)² + (y + 3)² = 4 qua ${\mathrm{T}}_{\overrightarrow{\mathrm{v}}}$.

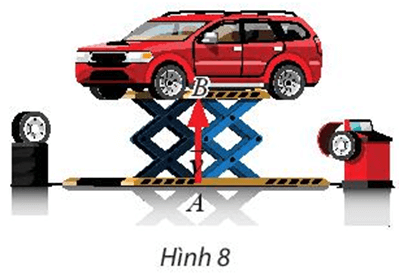
Trong Hình 8, người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép biến hình nào?

Cho phép tịnh tiến $T_{\overrightarrow{u}}$ và phép tịnh tiến $T_{\overrightarrow{v}}$. Với điểm M bất kì, $T_{\overrightarrow{u}}$ biến M thành M’, $T_{\overrightarrow{v}}$ biến M’ thành M’’. Hỏi có phép tịnh tiến nào biến điểm M thành M’’ không?

Cho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để $\overrightarrow{{\mathrm{MM}}^{\text{'}}}+\overrightarrow{\mathrm{MA}}=\overrightarrow{\mathrm{MB}}$ ?

Cho phép tịnh tiến $T_{\overrightarrow{u}}$ trong đó $\overrightarrow{u}=\left(3;5\right)$.

a) Tìm ảnh của các điểm A(–3; 4), B(2; –7) qua $T_{\overrightarrow{u}}$.

b) Biết rằng M’(2; 6) là ảnh của điểm M qua $T_{\overrightarrow{u}}$. Tìm tọa độ của điểm M.

c) Tìm ảnh của đường thẳng d: 4x – 3y + 7 = 0 qua $T_{\overrightarrow{u}}$.

Cho hai điểm B, C cố định trên đường tròn (O; R) và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.

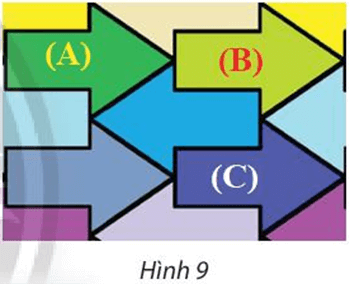
Trong Hình 9, tìm các vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ sao cho phép tịnh tiến $T_{\overrightarrow{u}}$ biến hình mũi tên (A) thành hình mũi tên (B) và phép tịnh tiến $T_{\overrightarrow{v}}$ biến hình mũi tên (A) thành hình mũi tên (C).