Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 4: Phép đối xứng tâm

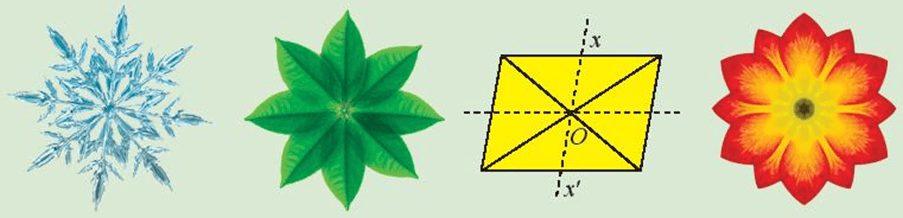
Trong các hình sau, hình nào có tâm đối xứng?

Tồn tại hay không phép biến hình biến mỗi hình phẳng sau đây thành chính nó?

Cho điểm O. Gọi f là quy tắc xác định như sau:

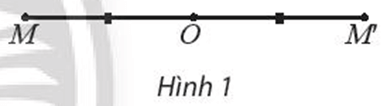
a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).

b) Với điểm M trùng với O thì f biến điểm M thành chính nó.

Hỏi f có phải là phép biến hình không?

Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm M’ = Đ_I(M), N’ = Đ_I(N), P’ = Đ_I(P).

Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó. 

Giả sử Đ_O là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua Đ_O. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.

Trong mặt phẳng tọa độ Oxy, tìm ảnh qua Đ_O của

a) điểm M(3; –4);

b) đường thẳng d: x – 3y + 6 = 0;

c) đường tròn (C): (x + 2)² + (y – 1)² = 4.

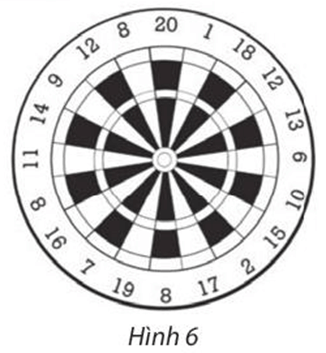
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.

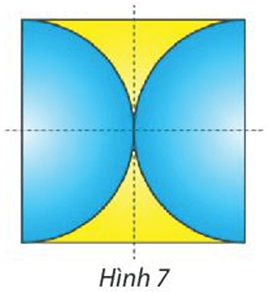
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.

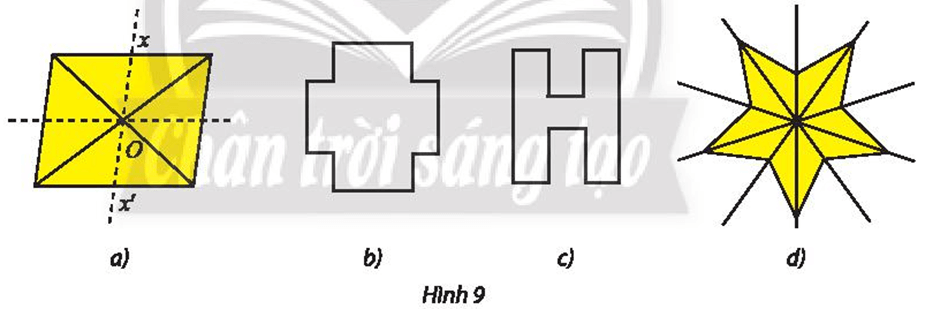
a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).

b) Nêu tên một hình có vô số tâm đối xứng.

Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình:

(C): x² + y² – 4x – 5 = 0. Viết phương trình ảnh của (C) qua phép đối xứng tâm O.

Cho đường tròn (O; R) và điểm I không nằm trên đường tròn. Với mỗi điểm A trên (O; R) ta xét hình vuông ABCD có tâm là I. Điểm C di động trên đường nào khi A di động trên đường tròn (O; R)?

Cho hình bình hành ABCD có AC cố định còn B di động trên (O; R). Hãy cho biết D di động trên đường nào.

Trong Hình 11, hình nào có trục đối xứng, hình nào có tâm đối xứng?

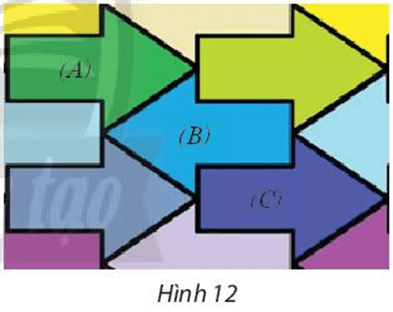
Trong Hình 12, tìm phép đối xứng biến hình mũi tên (A) thành hình mũi tên (B) và tìm phép đối xứng biến hình mũi tên (B) thành hình mũi tên (C).

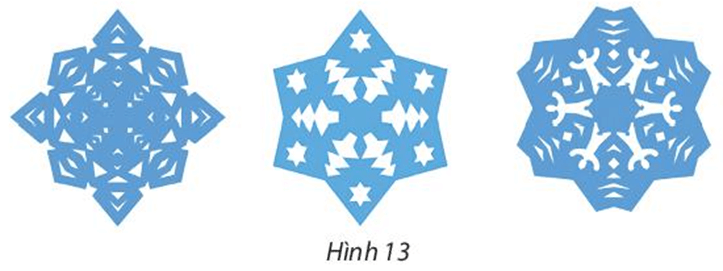
Nghệ thuật cắt giấy Kirigami của Nhật Bản đã sử dụng rất nhiều phép đối xứng khi cắt để tạo ra các hình đẹp. Hãy tìm trục đối xứng và tâm đối xứng của các hình trong Hình 13.

Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:

– Lấy một tờ giấy hình vuông, gấp đôi, gấp tư rồi gấp làm tám (Hình 14a).

– Vẽ hoa và lá trên bề mặt tam giác (Hình 14b).

– Dùng kéo cắt theo đường đã vẽ (Hình 14c).

– Trải phẳng tờ giấy ra để thấy hoa văn trang trí gồm hoa và lá (Hình 14d).

Tìm tâm đối xứng và trục đối xứng của hoa văn vừa làm.