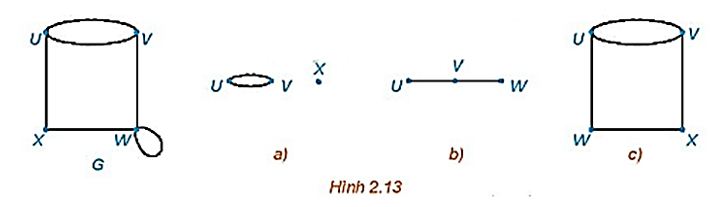Chuyên đề Toán 11 (Kết nối tri thức) Bài 8: Một vài khái niệm cơ bản

Trước khi vào một hồi nghị, các đại biểu bắt tay nhau (hai người bắt tay nhau nhiều nhất 1 lần). Có một đại biểu không bắt tay ai hết và thấy rằng có 4 người bắt tay 4 lần, 5 người bắt tay 5 lần và 6 người bắt tay 6 lần. Nếu hội nghị có đúng 16 đại biểu thì ông ta đếm nhầm. Vì sao có thể kết luận như vậy?

Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường, nhưng không là bạn của Dung; Dung là bạn của Cường, nhưng không là bạn của Bình; Bình là bạn của Cường.

a) Hãy biểu diễn mỗi bạn An, Bình, Cường, Dung bằng một điểm trên mặt phẳng và dùng chữ cái đầu (in hoa) trong tên của họ để đặt tên cho các điểm này.

b) Nếu hai người là bạn của nhau, hãy nối các điểm biểu diễn tương ứng bằng một đoạn thẳng (hay đoạn đường cong).

c) Từ hình vẽ thu được ở HĐ1b, hãy cho biết: ai có nhiều bạn nhất và ai có ít bạn nhất?

Bảng F của giải vô địch bóng đá thế giới World Cup 2018 gồm bốn đội: Đức, Hàn Quốc, Mexico và Thuỵ Điển. Biểu diễn các đội này bằng các điểm phân biệt kí hiệu lần lượt là D, H, M, T (vẽ sao cho không có ba điểm nào thẳng hàng để dễ quan sát) và nếu hai đội nào đấu với nhau thì ta nối hai điểm tương ứng bằng một đoạn thẳng, ta sẽ được một đồ thị G.

Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G.

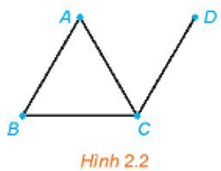
Xét đồ thị cho trong Hình 2.2.

a) Đồ thị trên có khuyên không?

b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?

Vẽ đồ thị G với các đỉnh và các cạnh như sau:

V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}.

G có phải là một đơn đồ thị không?

Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nào nối chúng không?

Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.

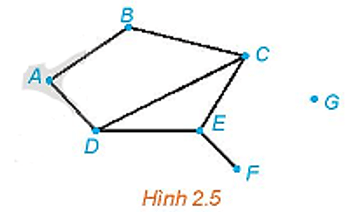
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.

Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.

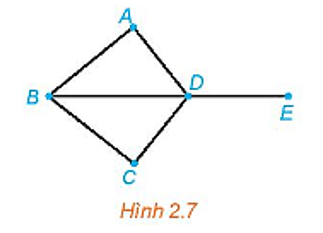
Cho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:

a) Đi từ đỉnh A đến đỉnh E.

b) Đi từ đỉnh A và lại quay về đỉnh A.

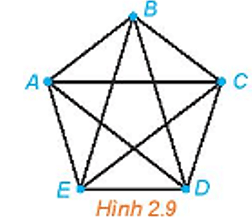
Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có: độ dài 4; độ dài 5.

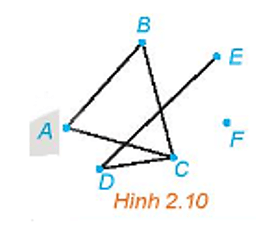
Trong đồ thị ở Hình 2.10, hãy:

a) Tìm một đường đi từ đỉnh A đến đỉnh E.

b) Có tồn tại một đường đi từ đỉnh A đến đỉnh F hay không?

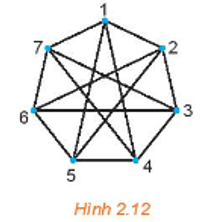
Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối đỉnh 1 và đỉnh 6.

Vẽ hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh

E(G) = {12; 14; 23; 25; 34; 35}.

Đồ thị G có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?

Hãy vẽ một đồ thị có 4 đỉnh và:

a) có đúng hai đỉnh cùng bậc và bậc là 1;

b) có đúng hai đỉnh cùng bậc và bậc là 2.

Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh của G và mọi cạnh của nó cũng là cạnh của G.

Những đồ thị nào trong các hình a), b), c) dưới đây là đồ thị con của đồ thị G?

Chứng minh rằng một đồ thị đầy đủ có n đỉnh thì có n(n−1)2𝑛𝑛−12 cạnh.

Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5. 

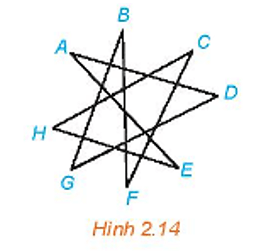
Cho đồ thị G như Hình 2.14.

a) Tìm một đường đi từ đỉnh A đến đỉnh B.

b) G có liên thông không?

c) Trong G có chu trình sơ cấp nào không?