Đề số 1
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Trong không gian vói hệ tọa độ Oxyz, đường thẳng đi qua điểm và vuông góc với mặt phẳng có phương trình là
Hàm số nào sau đây đồng biến trên khoảng
Tìm phần ảo của số phức
A. -2
B. 4i
C. 4
D.
Tìm tập xác định của hàm số
Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
B. Mỗi đỉnhlà đỉnh chung của ít nhất ba cạnh.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Biết F(x) là nguyên hàm của thỏa mãn Tính F(2)
Cho cấp số cộng có Khi đó bằng
A. -2020
B. -2006
C. 2019
D.
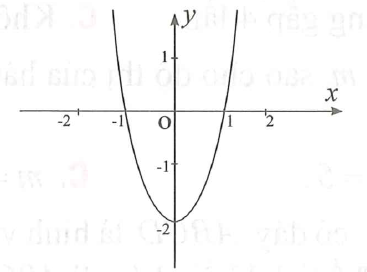
Đường cong như hình bên là đồ thị của hàm số nào sau đây?
Trong không gian Oxyz, tìm phương trình mặt phẳng (a) cắt ba trục Ox, Oy, Oz lần lượt tại 3 điểm
Biết rằng trong đó a và b là những số nguyên dương và phân số tối giản. Khi đó giá trị tổng của P = a+ tương ứng bằng
A. 23.
Số đường tiệm cận của đồ thị hàm số là
A. 1.
Cho hình nón có bán kính đáy và độ dài đường sinh Tính diện tích xung quanh của hình nón đã cho.
Tập nghiệm của bất phương trình là
Cho hàm số f(x) xác định trên R\{2} liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
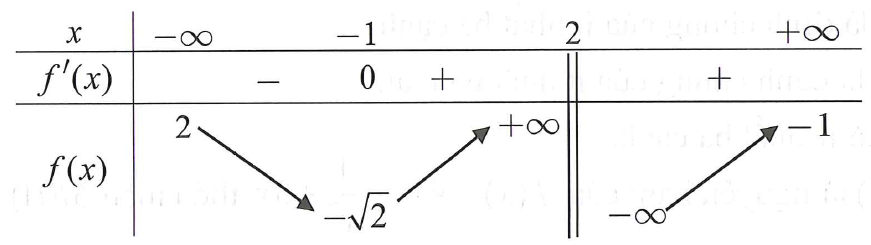
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f(x) = m có 3 nghiệm thực phân biệt.
A. (-1;1)
B. (-1;1]
Một khối trụ có bán kính R, chiều cao h và thể tích V1 Tăng bán kính đáy lên gấp đôi, chiều cao khối trụ không đổi thì thể tích khối trụ khi đó
A. Tăng gấp đôi.
Tìm giá trị của tham số m sao cho đồ thị của hàm số nhận điểm A(1;3) làm tâm đối xứng
A. m = 4
B. m = 5
C. m = 3
D. m = 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, . Góc giữa SC và (ABCD) là 45o Thể tích khối chóp S.ABCD là
Tìm tham số thực m để hàm số liên tục tại điểm
A. m = 4
B. m = 3
C. m = 2
D. m = 5
Cho hai số phức thỏa mãn Tính
C.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm H (1;-2;3) và cắt các trục tọa độ tại các điểm A, B và C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là
Cho và Khẳng định nào sau đây là đúng?
Cho đồ thị hàm số có 3 điểm cực trị là A, B, C. Biết M, N là hai điểm di động lần lượt thuộc các cạnh AB, AC sao cho diện tích tam giác ABC gấp 3 lần diện tích tam giác AMN. Giá trị nhỏ nhất của độ dài đoạn thẳng MN là
B.
D. 2
Tổng các nghiệm của phương trình bằng
Cho (với là phân số tối giản). Khẳng định nào sau đây là sai?
C.
Cho hàm số thỏa mãn và
Khẳng định nào đúng?
Cho số phức z thỏa mãn điều kiện Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là một hình phẳng có diện tích bằng
A.
D.
Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình tròn là 20 mét và 15 mét. Khoảng cách giữa hai tâm của hai hình tròn là 30 mét. Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 ngàn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 ngàn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào trong các số dưới đây?
Gọi là hai nghiệm phức của phương trình Giá trị của biểu thức bằng
Cho lăng trụ có ABCD là hình chữ nhật Tính thể tích khối lăng trụ biết rằng
D.
Cho ba điểm A, B, C lần lượt là điểm biểu diễn ba số phức với . Biết và Mệnh đề nào sau đây đúng?
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng
Cho tập Hỏi có tất cả bao nhiêu mệnh đề đúng trong các mệnh đề sau
(I) “Có số có 4 chữ số được lập từ tập X”
(II) “ là một tổ hợp chập 3 của X”
(III) “Mỗi hoán vị các phần tử của X là một chỉnh hợp chập 9 của X”
Cho hàm số Nếu là một nguyên hàm của hàm số và đồ thị hàm số đi qua thì là
D. 20.
Cho hàm số liên tục và nhận giá trị dương trên Biết với Tính giá trị
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt phẳng đi qua A, B và trung điểm M của SC. Mặt phẳng chia khối chóp đã cho thành hai phần có thể tích lần lượt là với Tính tỉ số
D.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và mặt cầu Số mặt phẳng chứa hai điểm và tiếp xúc với mặt cầu là
Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, và Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC.
Phương trình (với m là tham số thực) có tối đa bao nhiêu nghiệm thực?
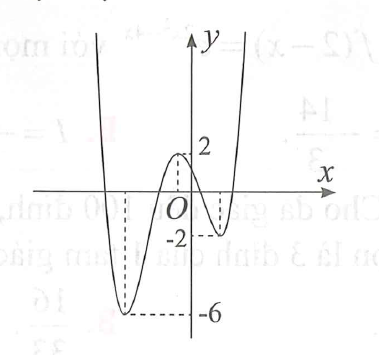
Cho đồ thị hàm số như hình vẽ dưới đây. Có bao nhiêu giá trị nguyên của tham số m để hàm số có 5 điểm cực trị?
Trong không gian với hệ tọa độ Oxyz, cho điểm và hai đường thẳng Phương trình đường thẳng đi qua M, cắt cả và là
Cho khối nón đỉnh O, trục OI. Mặt phẳng trung trực của OI chia khối nón thành hai phần. Tỉ số thể tích của hai phần là
Cho hình lăng trụ tam giác có thể tích là V và độ dài cạnh bên là Cho điểm thuộc cạnh sao cho Các điểm lần lượt thuộc cạnh sao cho Biết rằng thể tích khối đa diện bằng Giá trị của bằng
Biết rằng và Khi đó giá trị của biểu thức tương ứng bằng
Một kĩ sư được một công ty xăng dầu thuê thiết kế một mẫu bồn chứa xăng với thể tích V cho trước, hình dạng như hình bên, các kích thước r, h thay đổi sao cho nguyên vật liệu làm bồn xăng là ít nhất.
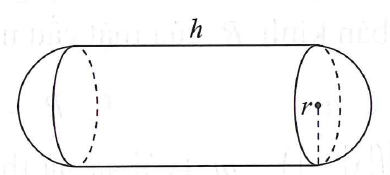
Người kĩ sư này phải thiết kế kích thước h như thế nào để đảm bảo được đúng yêu cầu mà công ty xăng dầu đã đưa ra?
Cho đa giác đều 100 đỉnh, chọn ngẫu nhiên 3 đỉnh của đa giác. Xác suất để 3 đỉnh được chọn là 3 đỉnh của 1 tam giác tù là
D.
Cho hai số thực thỏa mãn Giá trị nhỏ nhất của biểu thức bằng
D.
Cho hình hộp chữ nhật có Hai mặt phẳng và hợp với nhau góc Đường chéo hợp với mặt phẳng một góc β Hai góc thay đổi nhưng thỏa mãn hình hộp luôn là hình lăng trụ đều. Giá trị lớn nhất của thể tích khối hộp là