Đề số 23

Câu 1:

Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là:

A. $A_{30}^{3}$

B. 3³⁰

C. 10

D. $C_{30}^{3}$

Câu 2:

Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai d của cấp số cộng đó là bao nhiêu?

A. d = 4.

B. d = 5.

C. d = 6.

D. d = 7.

Câu 3:

Cho hàm số có bảng biến thiên như hình bên dưới.Mệnh đề nào sau đây đúng?

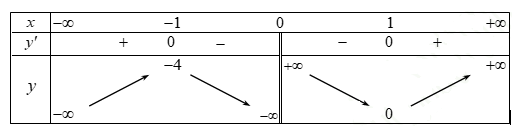
A. Hàm số đồng biến trên khoảng (0; $+ \infty) .$

B. Hàm số nghịch biến trên khoảng (-1;1).

C. Hàm số đồng biến trên khoảng (-1;0).

D. Hàm số nghịch biến trên khoảng (0;1).

Câu 4:

Cho hàm số y=f(x) có đồ thị

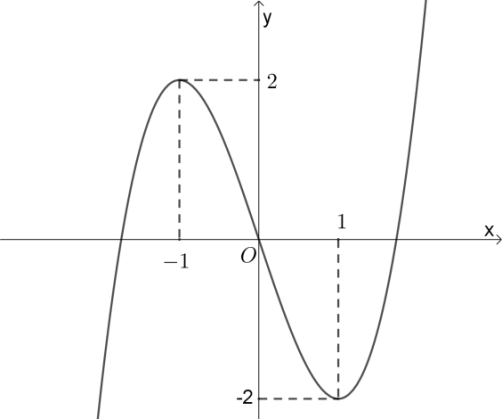
Media VietJack

Hàm số đã cho đạt cực đại tại

A. x = -1.

B. x = 2.

C. x = 1.

D. x = -2.

Câu 5:

Cho hàm số y=f(x) có đồ thị trên một khoảng K như hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?

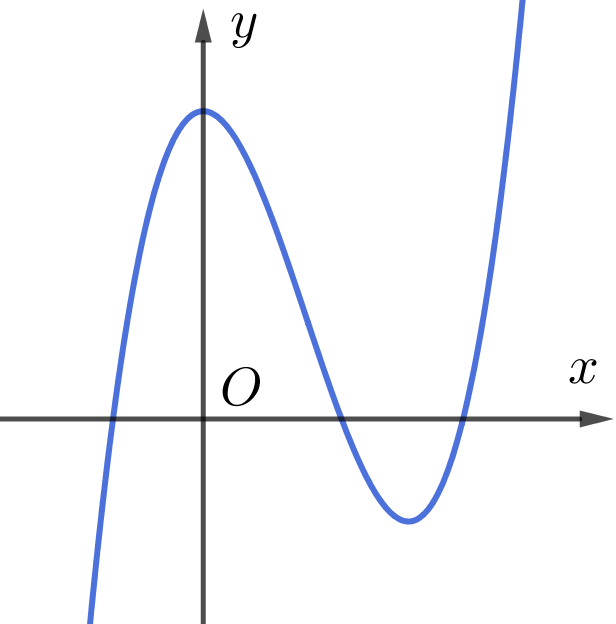
A. 3

B. 2

C. 0

D. 1

Câu 6:

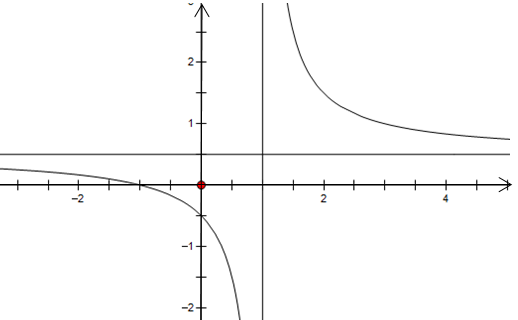
Đường tiệm cận ngang của đồ thị hàm số $y = \frac{2 x - 4}{x + 2}$ là

A. x = 2.

B. y = 2.

C. x = -2.

D. y = -2.

Câu 7:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. $y = \frac{x + 2}{2 x - 1}$

B. $y = \frac{2 x}{3 x - 3}$

C. $y = \frac{x + 1}{2 x - 2}$

D. $y = \frac{2 x - 4}{x - 1}$

Câu 8:

Tìm tung độ giao điểm của đồ thị

(C) : y = \frac{2 x - 3}{x + 3}

và đường thẳng d: y=x-1.

A. 1

B. -3

C. -1

D. 3

Câu 9:

Với a,b>0 tùy ý, mệnh đề nào dưới đây đúng?

A. log(ab)=loga.logb

B. log(ab²)=2loga+2logb

C. log(ab²)=loga+2logb

D. log(ab)=loga-logb

Câu 10:

Đạo hàm của hàm số y = 5^x + 2017 là:

A. $y' = \frac{5^{x}}{5 \ln 5}$

B. $y' = 5^{x} . \ln 5$

C. $y' = \frac{5^{x}}{\ln 5}$

D. $y' = 5^{x}$

Câu 11:

Cho a là số thực dương. Giá trị của biểu thức

P = a^{\frac{2}{3}} \sqrt{a}

bằng

A. $a^{\frac{5}{6}}$

B. $a^{5}$

C. $a^{\frac{2}{3}}$

D. $a^{\frac{7}{6}}$

Câu 12:

Tổng lập phương các nghiệm thực của phương trình

3^{x^{2} - 4 x + 5} = 9

là

A. 26

B. 27

C. 28

D. 25

Câu 13:

Tìm số nghiệm của phương trình

\log_{3} (2 x - 1) = 2

.

A. 1

B. 5

C. 2

D. 0

Câu 14:

Họ nguyên hàm của hàm số

f (x) = x^{2}

là

A. $\int x^{2} d x = \frac{x^{3}}{3} + C$

B. $\int x^{2} d x = \frac{x^{2}}{3} + C$

C. $\int x^{2} d x = \frac{x^{3}}{3}$

D. $\int x^{2} d x = 2 x + C$

Câu 15:

Một nguyên hàm của hàm số

f (x) = {(x + 1)}^{3}

là

A. $F (x) = 3 {(x + 1)}^{2}$ .

B. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

C. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

D. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

Câu 16:

Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-1;1] thỏa mãn

\int_{- 1}^{1} f^{'} (x) d x = 5

và f(-1)=4. Tìm f(1) .

A. f(1) = -1.

B. f(1) = 1

C. f(1) = 9

D. f(1) = -9

Câu 17:

Tích phân

I = \int_{1}^{2} (\frac{1}{x} + 2) d x

bằng

A. I = ln2 + 2.

B. I = ln2 + 1.

C. I = ln2 - 1.

D. I = ln2 + 3.

Câu 18:

Cho a,b là hai số thực thỏa mãn a+6i=2-2bi, với i là đơn vị ảo. Giá trị của a+b bằng

A. -1

B. 1

C. -4

D. 5

Câu 19:

Cho số phức

z_{1} = 3 + 2 i, z_{2} = 6 + 5 i

. Tìm số phức liên hợp của số phức

z = 6 z_{1} + 5 z_{2}

A. $z$ = 51 + 40i.

B. $z$ = 51 - 40i.

C. $z$ = 48 + 37i.

D. $z$ = 48 - 37i.

Câu 20:

Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z = -1 + 2i?

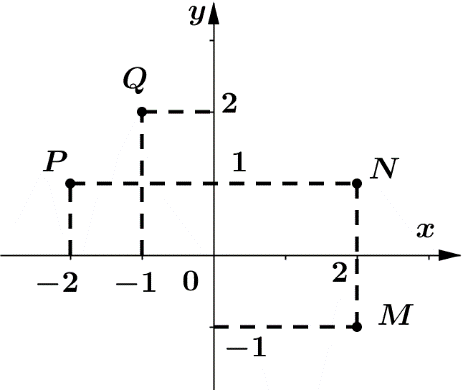
A. N

B. P

C. M

D. Q

Câu 21:

Thể tích của khối lập phương cạnh 2a bằng

A. 8a

B. 8a³

C. a³

D. 6a³

Câu 22:

Cho khối chóp có diện tích đáy bằng 6cm²và có chiều cao là 2cm. Thể tích của khối chóp đó là:

A. 6cm³

B. 4cm³

C. 3cm³

D. 12cm³

Câu 23:

Cho khối nón có bán kính đáy

r = \sqrt{3}

và chiều cao h=4. Tính thể tích V của khối nón đã cho.

A. $V = 16 π \sqrt{3}$ .

B. $V = 12 π$ .

C. $V = 4 π .$

D. 4.

Câu 24:

Tính thể tích V của khối trụ có bán kính đáy r=10cm và chiều cao h=6cm.

A. $V = 120 π {cm}^{3} .$

B. $V = 360 π {cm}^{3} .$

C. $V = 200 π {cm}^{3}$ .

D. $V = 600 π {cm}^{3}$ .

Câu 25:

Trong không gian với trục hệ tọa độ Oxyz, cho

\vec{a} = - \vec{i} + 2 \vec{j} - 3 \vec{k} .

Tọa độ của vectơ

\vec{a}

là:

A. $\vec{a} (- 1; 2; - 3$ ).

B. $\vec{a} (2; - 3; - 1$ ).

C. $\vec{a} (- 3; 2; - 1$ ).

D. $\vec{a} (2; - 1; - 3$ ).

Câu 26:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình

x^{2} + y^{2} + z^{2} + 4 x - 2 y - 4 = 0

.Tính bán kính R của (S).

A. 1

B. 9

C. 2

D. 3

Câu 27:

Trong không gian với hệ trục tọa độ Oxyz cho các điểm A(0;1;2) , B(2;-2;1) , C(-2;0;1) . Phương trình mặt phẳng đi qua A và vuông góc với BC là

A. 2x - y - 1 = 0.

B. -y + 2z - 3 = 0.

C. 2x - y + 1 = 0.

D. y + 2z - 5 = 0.

Câu 28:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;1); B(2;1;-1), véc tơ chỉ phương của đường thẳng AB là:

A. $\vec{u} = (1; - 1; - 2)$

B. $\vec{u} = (3; - 1; 0)$

C. $\vec{u} = (1; 3; - 2)$

D. $\vec{u} = (1; - 1; 0)$

Câu 29:

Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:

A. $\frac{13}{27}$ .

B. $\frac{14}{27} .$

C. $\frac{1}{2}$ .

D. $\frac{365}{729} .$

Câu 30:

Cho hàm số

y = \frac{2 x - 1}{x + 1}

. Mệnh đề nào dưới đây là đúng.

A. Hàm số nghịch biến trên các khoảng $(- \infty; - 1) v à (1; + \infty)$ .

B. Hàm số đồng biến trên các khoảng

(- \infty; - 1) v à (- 1; + \infty)

.

C. Hàm số luôn nghịch biến trên R.

D. Hàm số đồng biến trên R.

Câu 31:

Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

y = \frac{3 x - 1}{x - 3}

trên đoạn [0;2] . Tính 2M-m.

A. $2 M - m = \frac{- 14}{3}$

B. $2 M - m = \frac{- 13}{3}$

C. $2 M - m = \frac{17}{3}$

D. $2 M - m = \frac{16}{3}$

Câu 32:

Tập nghiệm của bất phương trình

\log_{2} (x - 1) \geq - 1

A. $[\frac{- 1}{2}; + \infty)$

B. $(- 1; - \frac{1}{2}]$

C. $(- \infty; - \frac{1}{2}]$

D. $[1; + \infty)$

Câu 33:

Cho

\int_{0}^{1} [f (x) - 2 g (x)] d x = 12

và

\int_{0}^{1} g (x) d x = 5

, khi đó

\int_{0}^{1} f (x) d x

bằng

A. -2.

B. 12.

C. 22.

D. 2.

Câu 34:

Cho hai số phức

z_{1} = 2 + i

và

z_{2} = - 3 + i

. Phần ảo của số phức

z_{1} \bar{z_{2}}

bằng

A. -5

B. -5i

C. 5

D. 5i

Câu 35:

Cho khối chóp S.ABC có

S A ⊥ (A B C)

, tam giác ABC vuông tại B, AC=2a, BC=a, SB=

2 a \sqrt{3}

. Tính góc giữa và mặt phẳng (SBC) .

A. 4 $5 °$ .

B. 3 $0 ° .$

C. 6 $0 ° .$

D. 9 $0 ° .$

Câu 36:

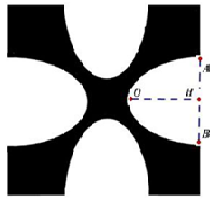
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng $a \sqrt{2} .$ Tính khoảng cách d từ O tâm của đáy ABCD

đến một mặt bên ttheo a.

A. $d = \frac{a \sqrt{5}}{2} .$

B. $d = \frac{a \sqrt{3}}{2} .$

C. $d = \frac{2 a \sqrt{5}}{3} .$

D. $d = \frac{a \sqrt{2}}{3} .$

Câu 37:

Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3) . Phương trình của mặt cầu có tâm I và đi qua A là

A. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 29 .$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5$ .

C. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 25 .$

D. $x + 1^{2} + y + 1^{2} + {(z + 1)}^{2} = 5$ .

Câu 38:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua hai điểm A(1;0;1) và B(3;2;-1) .

A. $\{\begin{cases} x = 1 + t \\ y = 1 + t \\ z = - 1 - t \end{cases}, t \in R$

B. $\{\begin{cases} x = 3 + t \\ y = 2 - t \\ z = - 1 - t \end{cases}, t \in R$

C. $\{\begin{cases} x = 1 - t \\ y = - t \\ z = 1 + t \end{cases}, t \in R$

D. $\{\begin{cases} x = 2 + t \\ y = 2 + t \\ z = - 2 - t \end{cases}, t \in R$

Câu 39:

Nếu hàm số f(x) có đạo hàm là

f^{'} (x) = x^{2} (x + 2) (x^{2} + x - 2) {(x - 1)}^{4}

thì điểm cực trị của hàm số f(x) là

A. x = 0.

B. x = 2.

C. x = 1.

D. x = -2.

Câu 40:

Số nghiệm nguyên của bất phương trình

{(17 - 12 \sqrt{2})}^{x} \geq {(3 + \sqrt{8})}^{x^{2}}

là

A. 3

B. 1

C. 2

D. 4

Câu 41:

Cho hàm số f(x) liên tục trên R và có

\int_{0}^{1} f (x) d x = 2, \int_{0}^{3} f (x) d x = 6

. Tính

I = \int_{- 1}^{1} f (| 2 x - 1 |) d x

.

A. I = 8

B. I = 16

C. I = 3/2

D. I = 4.

Câu 42:

Cho số phức z=a+bi (với

a, b \in ℝ

) thỏa |z|(2+i)=z-1+i(2z+3) . Tính S=a+b.

A. S = -1.

B. S = 1.

C. S = 7.

D. S = -5.

Câu 43:

Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác cân tại S và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc

60 °

. Tính thể tích khối chóp S.ABCD.

A. $\frac{a^{3} \sqrt{15}}{2}$

B. $\frac{a^{3} \sqrt{15}}{6}$

C. $\frac{a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3} \sqrt{3}}{6}$

Câu 44:

Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB=5cm, OH=4cm. Tính diện tích bề mặt hoa văn đó.

A. $\frac{160}{3} {cm}^{2}$

B. $\frac{140}{3} {cm}^{2}$

C. $\frac{14}{3} {cm}^{2}$

D. ${50cm}^{2}$

Câu 45:

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng

∆

là giao tuyến của hai mặt phẳng (P): z-1=0 và (Q): x+y+z-3=0. Gọi d là đường thẳng nằm trong mặt phẳng (P) , cắt đường thẳng

\frac{x - 1}{1} = \frac{y - 2}{- 1} = \frac{z - 3}{- 1}

và vuông góc với đường thẳng

∆

. Phương trình của đường thẳng d là

A. $\{\begin{cases} x = 3 + t \\ y = t \\ z = 1 + t \end{cases}$

B. $\{\begin{cases} x = 3 - t \\ y = t \\ z = 1 \end{cases}$

C. $\{\begin{cases} x = 3 + t \\ y = t \\ z = 1 \end{cases}$

D. $\{\begin{cases} x = 3 + t \\ y = - t \\ z = 1 + t \end{cases}$

Câu 46:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y=f(f(x)) có bao nhiêu điểm cực trị?

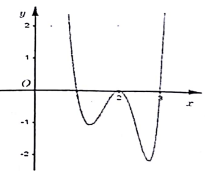
A. 6

B. 7

C. 8

D.9

Câu 47:

Cho

\log_{9} x = \log_{12} y = \log_{16} (x + y)

. Giá trị của tỷ số

\frac{x}{y}

là.

A. 2

B. $\frac{1 - \sqrt{5}}{2}$

C.1

D. $\frac{- 1 + \sqrt{5}}{2}$

Câu 48:

Cho hàm số y=f(x) . Hàm số y=f'(x) có đồ thị như hình vẽ. Biết phương trình f'(x)=0 có bốn nghiệm phân biệt a, 0, b, c với a<0<b<c.

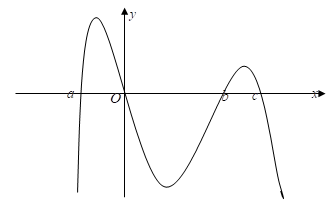
A. f(b) > f(a) > f(c).

B. f(a) > f(b) > f(c).

C. f(a) > f(c) > f(b).

D. f(c) > f(a) > f(b).

Câu 49:

Cho số phức z thỏa mãn |z-1-i| , số phức w thỏa mãn

|\bar{w} - 2 - 3 i| = 2

. Tìm giá trị nhỏ nhất của |z-w| .

A. $\sqrt{13} - 3$

B. $\sqrt{17} - 3$

C. $\sqrt{17} + 3$

D. $\sqrt{13} + 3$

Câu 50:

Trong không gian Oxyz, cho điểm $M (\frac{1}{2}; \frac{\sqrt{3}}{2}; 0)$ và mặt cầu $(S) : x^{2} + y^{2} + z^{2} = 8$ . Một đường thẳng đi qua điểm M và cắt (S) tại hai điểm phân biệt A, B. Diện tích lớn nhất của tam giác OAB bằng

A. 4

B. $2 \sqrt{7}$

C. $2 \sqrt{2}$

D. $\sqrt{7}$

Đề số 23

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề số 23

CHỌN BỘ SÁCH BẠN MUỐN XEM