Đề số 24

Câu 1:

Cho A là tập hợp gồm 20 điểm phân biệt. Số đoạn thẳng có hai điểm đầu mút phân biệt thuộc tập A là:

A. 170

B. 160

C. 190

D. 360

Câu 2:

Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm công bội q của cấp số nhân đã cho.

A. q = 3.

B. q = -3.

C. q = 2.

D. q = -2.

Câu 3:

Cho hàm số y=f(x) có bảng biến thiên bên dưới.

Media VietJack

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (0;1).

B. $(- \infty; 0)$ .

C. $(1; + \infty)$ .

D. (-1;0).

Câu 4:

Cho hàm số có bảng biến thiên như sau

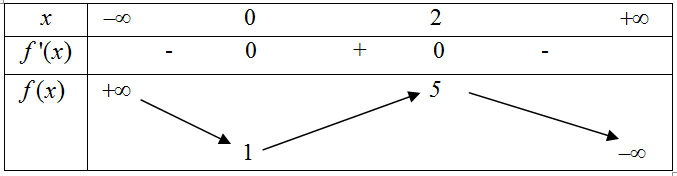
Media VietJack

Hàm số có cực đại là

A. y = 5.

B. x = 2.

C. x = 0.

D. y = 1.

Câu 5:

Cho hàm số y=f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y=f(x) trên đoạn [-2;3] .

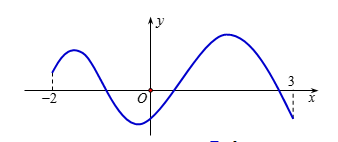
A. 1

B. 0

C. 2

D. 3

Câu 6:

Đồ thị hàm số

y = \frac{x + 1}{2 - x}

có tiệm cận ngang là đường thẳng:

A. y = 2.

B. y = -1.

C. y = $\frac{1}{2} .$

D. x = 2.

Câu 7:

Đường cong ở hình bên là đồ thị của hàm số nào?

A. $f (x) = x^{4} - 2 x^{2}$ .

B. $f (x) = x^{4} + 2 x^{2}$ .

C. $f (x) = - x^{4} + 2 x^{2} - 1$ .

D. $f (x) = - x^{4} + 2 x^{2} .$

Câu 8:

Số giao điểm của đồ thị hàm số

y = x^{3} - 3 x + 1

và trục hoành là

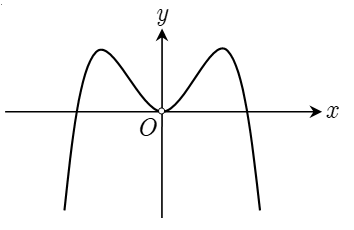
A. 3

B. 0

C. 2

D. 1

Câu 9:

Với a là số thực dương,

\log_{3}^{2} (a^{2})

bằng:

A. $2 \log_{3}^{2} a$ .

B. $4 \log_{3}^{2} a .$

C. $4 \log_{3} a .$

D. $\frac{4}{9} \log_{3} a$ .

Câu 10:

Tính đạo hàm của hàm số

y = \frac{1}{5} e^{4 x}

.

A. $y^{'} = \frac{1}{20} e^{4 x}$ .

B. $y^{'} = - \frac{4}{5} e^{4 x}$ .

C. $y^{'} = \frac{4}{5} e^{4 x}$ .

D. $y^{'} = - \frac{1}{20} e^{4 x} .$

Câu 11:

Cho a là số thực dương. Giá trị rút gọn của biểu thức

P = a^{\frac{4}{3}} \sqrt{a}

bằng

A. $a^{\frac{7}{3}} .$

B. $a^{\frac{5}{6}} .$

C. $a^{\frac{11}{6}} .$

D. $a^{\frac{10}{3}} .$

Câu 12:

Số nghiệm của phương trình

2^{2 x^{2} - 7 x + 5} = 1

là

A. 0

B. 3

C. 2

D. 1

Câu 13:

Tìm tập nghiệm S của phương trình

\log_{2} (x^{2} - 2) + 2 = 0

.

A. $S = \{- \frac{2}{3}; \frac{2}{3}\} .$

B. $S = \{- \frac{3}{2}; \frac{3}{2}\} .$

C. $S = \{\frac{2}{3}\} .$

D. $S = \{\frac{3}{2}\} .$

Câu 14:

Một nguyên hàm của hàm số f(x)=2x+1 là

A. $F (x) = x^{2} + x$ .

B. $F (x) = x^{2} + 1 .$

C. $F (x) = x^{2} + 1 .$

D. $F (x) = x^{2} + 1 .$

Câu 15:

Họ nguyên hàm của hàm số f(x) = x - sin2x là

A. $\int f (x) d x = \frac{x^{2}}{2} + \cos 2 x + C .$

B. $\int f (x) d x = \frac{x^{2}}{2} + \frac{1}{2} \cos 2 x + C .$

C. $\int f (x) d x = x^{2} + \frac{1}{2} \cos 2 x + C .$

D. $\int f (x) d x = \frac{x^{2}}{2} - \frac{1}{2} \cos 2 x + C .$

Câu 16:

Cho

\int_{a}^{c} f (x) d x = 50, \int_{b}^{c} f (x) d x = 20

. Tính

\int_{b}^{a} f (x) d x

.

A. -30.

B. 0.

C. 70.

D. 30.

Câu 17:

Tính tích phân

\int_{0}^{π} \sin 3 x d x

A. $- \frac{1}{3} .$

B. $\frac{1}{3} .$

C. $- \frac{2}{3} .$

D. $\frac{2}{3} .$

Câu 18:

Số phức z=5-6i có phần ảo là

A. 6

B. -6i

C. 5

D. -6

Câu 19:

Cho hai số phức $z_{1} = 1 + 2 i, z_{2} = 2 - 3 i$ . Xác định phần thực, phần ảo của số phức $z = z_{1} + z_{2}$ .

A. Phần thực bằng 3; phần ảo bằng -5.

B. Phần thực bằng 5; phần ảo bằng 5.

C. Phần thực bằng 3; phần ảo bằng 1.

D. Phần thực bằng 3; phần ảo bằng 1.

Câu 20:

Điểm M là biểu diễn của số phức z trong hình vẽ bên dưới. Chọn khẳng định đúng

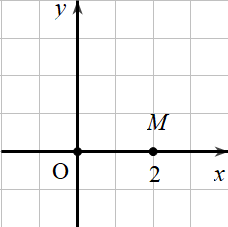
A. z = 2i

B. z =0

C. z = 2

D. z = 2 + 2i

Câu 21:

Khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích khối chóp đã cho bằng

A. $\frac{4}{3} a^{3}$

B. $\frac{16}{3} a^{3}$

C. $4 a^{3}$

D. $16 a^{3}$

Câu 22:

Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể tích của khối lăng trụ đó.

A. $\frac{a^{3} \sqrt{6}}{12} .$

B. $\frac{a^{3} \sqrt{6}}{4} .$

C. $\frac{a^{3} \sqrt{3}}{12} .$

D. $\frac{a^{3} \sqrt{3}}{4} .$

Câu 23:

Một khối nón có chiều cao bằng 3a, bán kính 2a thì có thể tích bằng

A. $2 π a^{3} .$

B. $12 π a^{3} .$

C. $6 π a^{3} .$

D. $4 π a^{3} .$

Câu 24:

Cho khối trụ tròn xoay có bán kính đáy bằng 3a, chiều cao bằng 4a, với

0 < a \in ℝ

. Thể tích của khối trụ tròn xoay đã cho bằng

A. $48 π a^{3} .$

B. $18 π a^{3} .$

C. $36 π a^{3} .$

D. $12 π a^{3} .$

Câu 25:

Trong không gian Oxyz, cho hai điểm A(1;1;-1) , B(2;3;2). Vectơ

\vec{A B}

có tọa độ là

A. (1;2;3).

B. (-1;-2;3).

C. (3;5;1).

D. (3;4;1).

Câu 26:

Trong không gian Oxyz, mặt cầu

{(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 4

có tâm và bán kính lần lượt là

A. I(1;2;-3), R=2.

B. I(-1;-2;3); R=2.

C. I(1;2;-3), R=4.

D. I(-1;-2;3), R=4.

Câu 27:

Phương trình mặt phẳng (P) đi qua điểm M(-1;2;0) và có vectơ pháp tuyến $\vec{n} = (4; 0; - 5)$ là

A. 4x - 5y - 4 = 0.

B. 4x - 5z - 4 = 0.

C. 4x - 5y + 4 = 0.

D. 4x - 5z + 4 = 0.

Câu 28:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng

d : \{\begin{cases} x = 1 \\ y = 2 + 3 t \\ z = 5 - t \end{cases}

. Vectơ chỉ phương của d là

A. $\vec{u_{2}} = (1; 3; - 1)$

B. $\vec{u_{2}} = (0; 3; - 1)$

C. $\vec{u_{4}} = (1; 2; 5)$

D. $\vec{u_{3}} = (1; - 3; - 1)$

Câu 29:

Gieo đồng tiền hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần

A. $\frac{1}{4} .$

B. $\frac{1}{2} .$

C. $\frac{3}{4} .$

D. $\frac{1}{3} .$

Câu 30:

Hàm số

f (x) = x^{4} - 2

nghịch biến trên khoảng nào?

A. $(- \infty; \frac{1}{2})$

B. $(0; + \infty)$

C. $(- \infty; 0)$

D. $(\frac{1}{2}; + \infty)$

Câu 31:

Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

f (x) = x^{3} - 3 x^{2} - 9 x + 35

trên đoạn [-4;4]. Tính M+2m

A. M + 2m = -1

B. M + 2m = 39

C. M + 2m = -41

D. M + 2m = -40

Câu 32:

Tập nghiệm của bất phương trình

{(\frac{1}{2})}^{x} > 4

là

A. $(- 2; + \infty) .$

B. $(- \infty; - 2) .$

C. $(- \infty; 2) .$

D. $(2; + \infty)$ .

Câu 33:

Cho

\int_{1}^{2} [4 f (x) - 2 x] d x = 1

. Khi đó bằng

\int_{1}^{2} f (x) d x

:

A. 1

B. -3

C. 3

D. -1

Câu 34:

Cho số phức z thỏa mãn (1+2i)z=(1+2i)-(-2+i) . Mô đun của z bằng

A. 2

B. 1

C. $\sqrt{2}$

D. $\sqrt{10}$

Câu 35:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc mặt đáy và SA=a. Gọi

φ

là góc tạo bởi SB và mặt phẳng (ABCD) . Xác định cot

φ

?

A. $\cot φ = 2$

B. $\cot φ = \frac{1}{2}$

C. $\cot φ = 2 \sqrt{2}$

D. $\cot φ = \frac{\sqrt{2}}{4}$

Câu 36:

Cho hình chóp S.ABC có ABC là tam giác vuông tại B,

S A ⊥ (A B C)

. Khoảng cách từ điểm A đến mặt phẳng (SBC) là:

A. Độ dài đoạn AC.

B. Độ dài đoạn AB.

C. Độ dài đoạn AH trong đó H là hình chiếu vuông góc của A trên SB.

D. Độ dài đoạn AM trong đó M là trung điểm của SC.

Câu 37:

Trong không gian Oxyz, cho hai điểm A(1;2;3) và B(3;2;1) . Phương trình mặt cầu đường kính AB là

A. ${(x - 2)}^{2} + {(y - 2)}^{2} + {(z - 2)}^{2} = 2$

B. ${(x - 2)}^{2} + {(y - 2)}^{2} + {(z - 2)}^{2} = 4$

C. $x^{2} + y^{2} + z^{2} = 2$

D. ${(x - 1)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

Câu 38:

Trong không gian với hệ trục Oxyz, cho tam giác ABC có A(-1;3;2), B(2;0;5) và C(0;-2;1) . Phương trình trung tuyến AM của tam giác ABC là.

A. $\frac{x + 1}{- 2} = \frac{y - 3}{- 2} = \frac{z - 2}{- 4}$

B. $\frac{x + 1}{2} = \frac{y - 3}{- 4} = \frac{z - 2}{1}$

C. $\frac{x - 2}{- 1} = \frac{y + 4}{3} = \frac{z - 1}{2}$

D. $\frac{x - 1}{2} = \frac{y + 3}{- 4} = \frac{z + 2}{1}$

Câu 39:

Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số

y = |\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m - 20|

trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng

A. 210

B. -195

C. 105

D. 300

Câu 40:

Có bao nhiêu số tự nhiên x không vượt quá 2018 thỏa mãn $\log_{2} (\frac{x}{4}) \log_{2}^{2} x \geq 0$ ?

A.2017

B.2016

C. 2014

D. 2015

Câu 41:

Cho hàm số y=f(x) có đạo hàm liên tục trên . Đồ thị hàm số y=f(x) như hình vẽ bên. Khi đó giá trị của biểu thức

\int_{0}^{4} f' (x - 2) d x + \int_{0}^{2} f' (x - 2) d x

bằng bao nhiêu

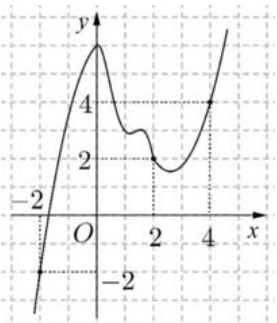
A.2

B. -2

C. 10

D. 6

Câu 42:

Tính tổng S của các phần thực của tất cả các số phức z thỏa mãn điều kiện

\bar{z} = \sqrt{3} z^{2} .

A. $S = \sqrt{3} .$

B. $S = \frac{\sqrt{3}}{6} .$

C. $S = \frac{2 \sqrt{3}}{3} .$

D. $S = \frac{\sqrt{3}}{3} .$

Câu 43:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) , góc giữa SB với mặt phẳng (ABCD) bằng

60 °

. Thể tích khối chóp S.ABCD là

A. $\frac{a^{3}}{\sqrt{3}}$

B. $\frac{a^{3}}{3 \sqrt{3}}$

C. $\sqrt{3} a^{3}$

D. $3 \sqrt{3} a^{3}$

Câu 44:

Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số tiền bác Năm phải trả là:

A. 33750000 đồng.

B. 12750000 đồng.

C. 6750000 đồng.

D. 3750000 đồng.

Câu 45:

Trong không gian Oxyz, đường thẳng đi qua điểm M(1;2;2) , song song với mặt phẳng (P): x - y + z + 3 = 0 đồng thời cắt đường thẳng

d : \frac{x - 1}{1} = \frac{y - 2}{1} = \frac{z - 3}{1}

có phương trình là

A. $\{\begin{cases} x = 1 - t \\ y = 2 - t \\ z = 2 \end{cases}$

B. $\{\begin{cases} x = 1 - t \\ y = 2 - t \\ z = 3 - t \end{cases}$

C. $\{\begin{cases} x = 1 + t \\ y = 2 - t \\ z = 3 \end{cases}$

D. $\{\begin{cases} x = 1 - t \\ y = 2 + t \\ z = 3 \end{cases}$

Câu 46:

Cho hàm số y=f(x) và đồ thị hình bên là đồ thị của đạo hàm f'(x). Hỏi đồ thị của hàm số

g (x) = |2 f (x) - {(x - 1)}^{2}|

có tối đa bao nhiêu điểm cực trị ?

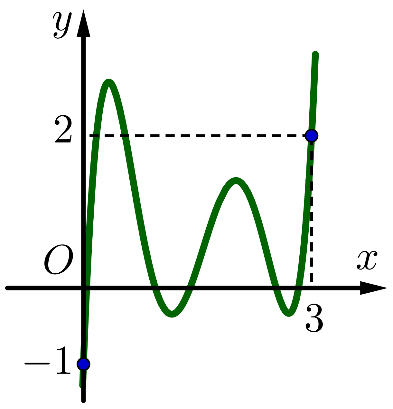
A. 9

B. 11

C. 8

D. 7

Câu 47:

Cho phương trình

\log_{2} (5^{x} - 1) . \log_{4} ({2.5}^{x} - 2) = m

. Hỏi có bao nhiêu giá trị nguyên m để phương trình có nghiệm thuộc đoạn

[1; \log_{5} 9]

?

A. 4

B. 5

C. 2

D. 3

Câu 48:

Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và đồ thị của f'(x) trên đoạn [-2;6] như hình bên dưới. Khẳng định nào dưới đây đúng?

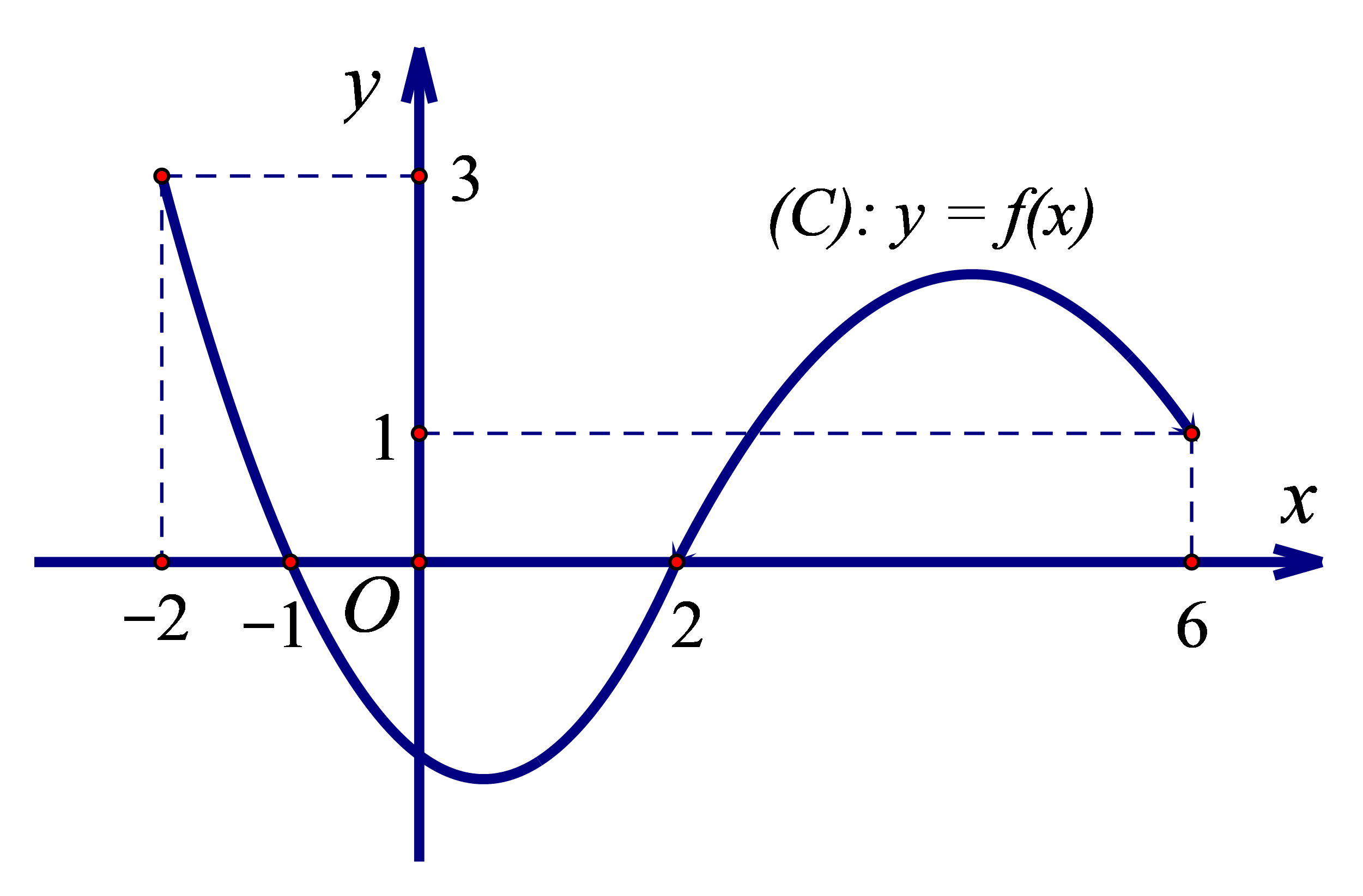
A. f(-2) < f(-1) < f(2) < f(6)

B. $f (2) < f (- 2) < f (- 1) < f (6)$

C. $f (- 2) < f (2) < f (- 1) < f (6)$

D. $f (6) < f (2) < f (- 2) < f (- 1)$

Câu 49:

Cho hai số phức z₁, z₂ thỏa mãn

|z_{1} + 1 - i| = 2 và z_{2} = i z_{1}

. Tìm giá trị nhỏ nhất

|z_{1} - z_{2}|

của biểu thức ?

A. $m = \sqrt{2} - 1$

B. $m = 2 \sqrt{2}$

C. m = 2

D. $m = 2 \sqrt{2} - 2$

Câu 50:

Trong không gian Oxyz, cho mặt phẳng (P): x+2y+2z+4=0 và mặt cầu

(S) : x^{2} + y^{2} + z^{2} - 2 x - 2 y - 2 z - 1 = 0.

Giá trị của điểm M trên (S) sao cho d(M,(P))) đạt GTNN là

A. (1;1;3)

B. $(\frac{5}{3}; \frac{7}{3}; \frac{7}{3})$

C. $(\frac{1}{3}; - \frac{1}{3}; - \frac{1}{3})$

D. (1;-2;1)

Đề số 24

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề số 24

CHỌN BỘ SÁCH BẠN MUỐN XEM