Đề số 25

Câu 1:

Một tổ học sinh có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn 4 học sinh của tổ đó tham gia đội xung kích?

A. 4!

B. $C_{5}^{4} + C_{7}^{4}$

C. $A_{12}^{4}$

D. $C_{12}^{4}$

Câu 2:

Cấp số cộng (u_n) có số hạng tổng quát $u_{n} = 2 n + 3.$ Số hạng thứ 10 có giá trị bằng

A. 23

B. 280

C. 140

D. 20

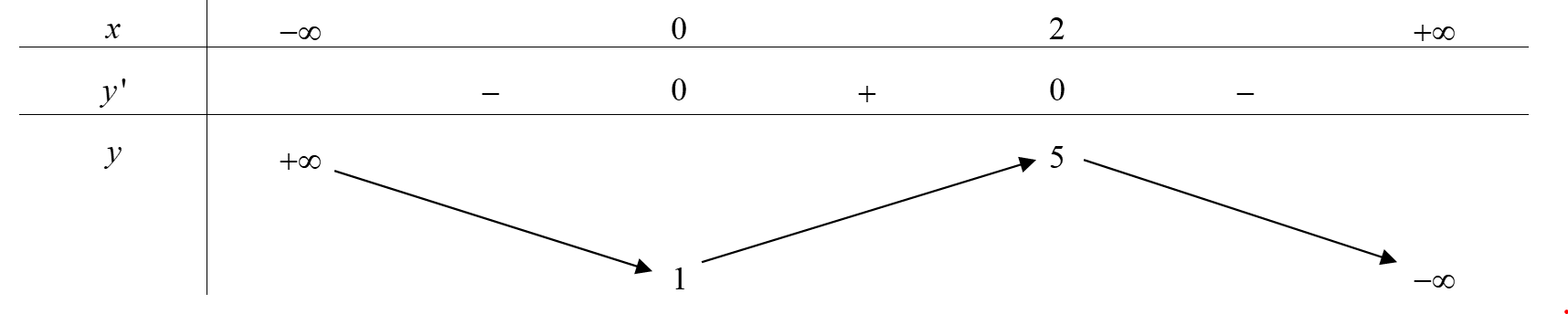
Câu 3:

Hàm số y=f(x) có bảng biến thiên như hình bên. Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?

A. $(- \infty; 0)$

B. $(2; + \infty)$

C. (1;5)

D. (0;2)

Câu 4:

Cho hàm số y=f(x) có bảng biến thiên như sau

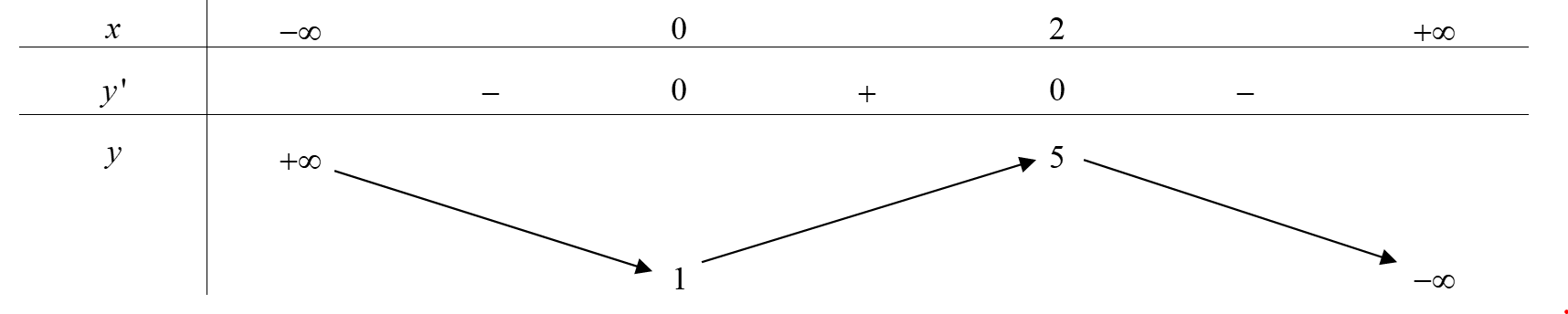
Hàm số đạt cực tiểu tại điểm

A. x = 5.

B. x = 2.

C. x = 1.

D. x = 0.

Câu 5:

Cho hàm số y=f(x) có đạo hàm trên R Biết rằng hàm số y=f'(x) có đồ thị như hình bên. Đặt g(x)=f(x)+x Hỏi hàm số có bao nhiêu điểm cực đại và bao nhiêu điểm cực tiểu?

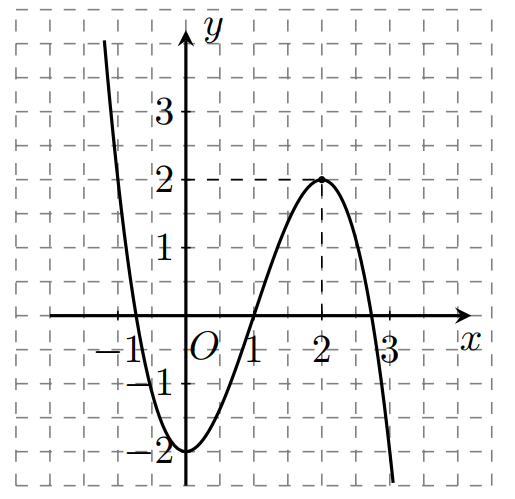
A. Hàm số có một điểm cực đại và hai điểm cực tiểu.

B. Hàm số không có điểm cực đại và có một điểm cực tiểu.

C. Hàm số có một điểm cực đại và một điểm cực tiểu.

D. Hàm số có hai điểm cực đại và một điểm cực tiểu.

Câu 6:

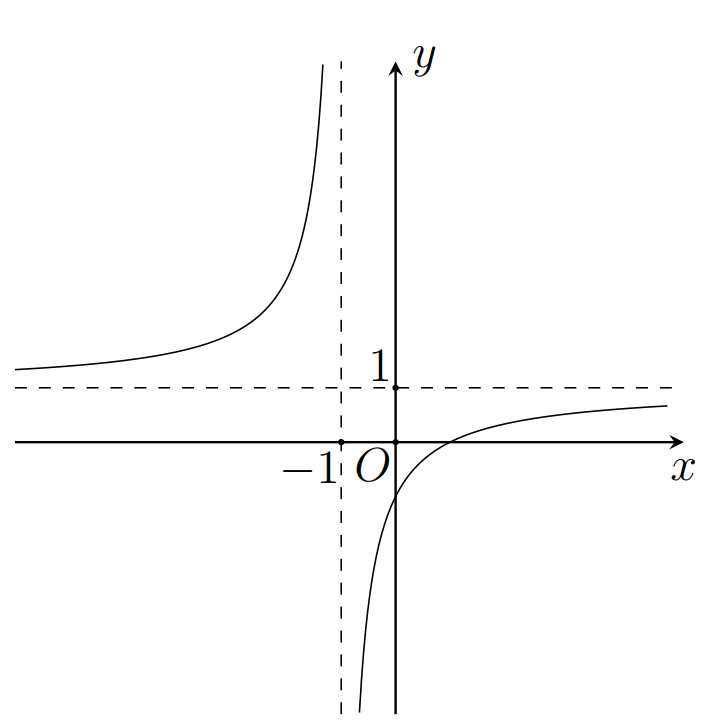
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y = \frac{x - 3}{3 x - 2} .$

A. $x = \frac{1}{3} .$

B. $x = \frac{2}{3} .$

C. $y = \frac{2}{3} .$

D. $y = \frac{1}{3} .$

Câu 7:

Đường cong trong hình bên phải là đồ thị của hàm số nào dưới đây?

A. $y = \frac{x - 1}{x + 1} .$

B. $y = x^{4} - 2 x^{2} - 1.$

C. $y = x^{3} - 3 x^{2} + 2.$

D. $y = \frac{x + 1}{x - 1} .$

Câu 8:

Tọa độ giao điểm của đồ thị các hàm số

y = \frac{x^{2} - 2 x - 3}{x - 2}

và y=x+1 là

A. (-1;0)

B. (3;1)

C. (2;-3)

D. (2;2)

Câu 9:

Với a là số thực dương tùy ý, $\log_{3} (3 a)$ bằng

A. $3 \log_{3} a$ .

B. $3 + \log_{3} a .$

C. $1 + \log_{3} a .$

D. $1 - \log_{3} a .$

Câu 10:

Tính đạo hàm của hàm số

y = \sin 2 x + 3^{x} .

A. $y' = 2 \cos 2 x + x 3^{x} - 1.$

B. $y' = - \cos 2 x + 3^{x} .$

C. $y' = - 2 \cos 2 x - 3^{x} \ln 3.$

D. $y' = 2 \cos 2 x + 3^{x} \ln 3.$

Câu 11:

Cho

0 < a \neq 1; α, β \in ℝ .

Trong các mệnh đề sau, mệnh đề nào đúng?

A. $\frac{a^{α}}{a^{β}} = a^{\frac{α}{β}}$

B. $a^{\sqrt{α}} = {(\sqrt{a})}^{α} (α > 0)$

C. $a^{α^{β}} = {(a^{α})}^{β}$

D. $\sqrt{a^{α}} = {(\sqrt{a})}^{α}$

Câu 12:

Tìm nghiệm của phương trình $\log_{25} (x + 1) = \frac{1}{2} .$

A. x = 4.

B. x = 6.

C. x = 24.

D. x = 0.

Câu 13:

Tìm nghiệm thực của phương trình

2^{x} = 7.

A. $x = \sqrt{7}$

B. $x = \frac{7}{2} .$

C. $x = \log_{2} 7.$

D. $x = \log_{7} 2.$

Câu 14:

Họ nguyên hàm của hàm số

f (x) = 2 x^{2} + x + 1

là

A. $\frac{2 x^{3}}{3} + x^{2} + x + C .$

B. 4x + 1.

C. $\frac{2 x^{3}}{3} + \frac{x^{2}}{2} + x .$

D. $\frac{2 x^{3}}{3} + \frac{x^{2}}{2} + x + C .$

Câu 15:

Hàm số f(x)=cox(4x+7) có một nguyên hàm là

A. -sin(4x + 7) + x.

B. $\frac{1}{4} \sin (4 x + 7) - 3.$

C. sin(4x + 7) - 1.

D. $- \frac{1}{4} \sin (4 x + 7) + 3.$

Câu 16:

Cho

I = \int_{- 2}^{3} \frac{2 x - 3}{x - 4} d x = a + b \ln 6

với

a, b \in ℤ .

Tính a-b

A. 15

B. 17

C. 7

D. 10

Câu 17:

Tích phân

\int_{0}^{3} (2 x + 1) d x

bằng

A. 6

B. 9

C. 12

D. 3

Câu 18:

Cho số phức z = 1 + 2i. Mô-đun của z là

A. 3

B. $\sqrt{5}$

C. 5

D. 4

Câu 19:

Cho hai số phức z₁= 2 - 7i và z₂= -4 + i. Điểm biểu diễn số phức $z_{1} + z_{2}$ trên mặt phẳng tọa độ là điểm nào dưới đây?

A. Q(-2;-6)

B. P(-5;-3)

C. N(6;-8)

D. M(3;-11)

Câu 20:

Điểm M trong hình bên dưới là điểm biểu diễn của số phức

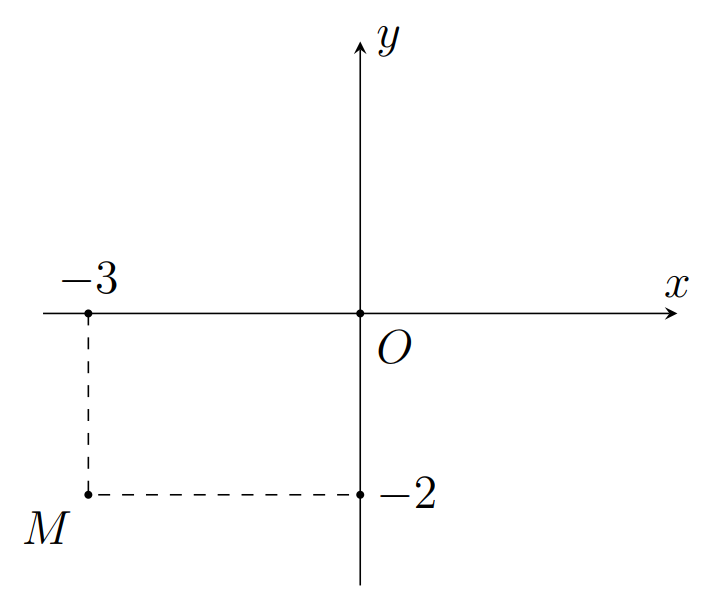
Media VietJack

A. z = -3 + 2i

B. z = 3 + 2i

C. z = -3 - 2i

D. z = 3 - 2i

Câu 21:

Cho hình trụ có diện tích đáy là B chiều cao là h và thể tích là V. Chọn công thức đúng?

A. B = V.h.

B. $V = \frac{1}{3} h B .$

C. $V = \frac{3 V}{B} .$

D. V = h.B.

Câu 22:

Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là

A. $V = \frac{1}{3} B h .$

B. V = B.h.

C. $V = \frac{1}{6} B h .$

D. V = 3B.h.

Câu 23:

Tính thể tích khối trụ có bán kính R=3 chiều cao h=5.

A. $V = 45 π .$

B. V = 45.

C. $V = 15 π .$

D. $V = 90 π .$

Câu 24:

Mặt cầu bán kính R nội tiếp trong một hình lập phương. Hãy tính thể tích V của hình lập phương đó.

A. $V = \frac{8 π R^{3}}{3} .$

B. $V = \frac{16 π R^{3}}{3} .$

C. $V = 16 R^{3} .$

D. $V = 8 R^{3} .$

Câu 25:

Hình chiếu vuông góc của điểm M(1;2;-4) trên mặt phẳng Oxy là điểm có tọa độ?

A. (1;2;0)

B. (1;2;-4)

C. (0;2;-4)

D. (1;0;-4)

Câu 26:

Trong không gian tọa độ Oxyz xác định phương trình mặt cầu có tâm I(3;-1;2) và tiếp xúc mặt phẳng (P): x+2y-2z=0

A. ${(x - 3)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4 .$

B. ${(x - 3)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 1.$

C. ${(x + 3)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 1.$

D. ${(x + 3)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 4 .$

Câu 27:

Trong không gian Oxyz mặt phẳng (P) đi qua điểm A(-1;2;0) và nhận

\vec{n} = (- 1; 0; 2)

làm một véc tơ pháp tuyến có phương trình là

A. -x + 2y - 5 = 0.

B. x + 2z -5 = 0.

C. -x + 2y - 5 = 0.

D. x - 2z + 1 = 0.

Câu 28:

Trong không gian Oxyz một véc-tơ chỉ phương của đường thẳng chứa trục Oy có tọa độ là

A. (0;1;2020)

B. (1;1;1)

C. (0;2020;0)

D. (1;0;0)

Câu 29:

Một nhóm gồm 10 học sinh trong đó có An và Bình, đứng ngẫu nhiên thành một hàng. Xác suất để An và Bình đứng cạnh nhau là

A. $\frac{2}{5}$

B. $\frac{1}{10}$

C. $\frac{1}{5}$

D. $\frac{1}{4}$

Câu 30:

Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

A. $y = x^{3} - 3 x^{2} + 3$

B. $y = x^{4} - 2 x^{2} + 1.$

C. $y = - x^{4} + 2 x^{2} + 1.$

D. $y = - x^{3} + 3 x^{2} + 1.$

Câu 31:

Giá trị nhỏ nhất của hàm số

y = \frac{x - 1}{x + 1}

trên đoạn [0;3] là:

A. $\min_{x \in [0; 3]} y = \frac{1}{2} .$

B. $\min_{x \in [0; 3]} y = - 3.$

C. $\min_{x \in [0; 3]} y = - 1.$

D. $\min_{x \in [0; 3]} y = 1.$

Câu 32:

Tập nghiệm S của bất phương trình

\log_{2} (x - 1) < 3

là

A. S = (1;10)

B. S = ( $- \infty; 9)$

C. S = ( $- \infty; 10)$

D. S = (1;9)

Câu 33:

Biết

\int_{2}^{3} \frac{x^{2} - 3 x + 2}{x^{2} - x + 1} d x = a \ln 7 + b \ln 3 + c \ln 2 + d

(với a,b,c,d là các số nguyên). Tính giá trị của biểu thức

T = a + 2 b^{2} + 3 c^{3} + 4 d^{4} .

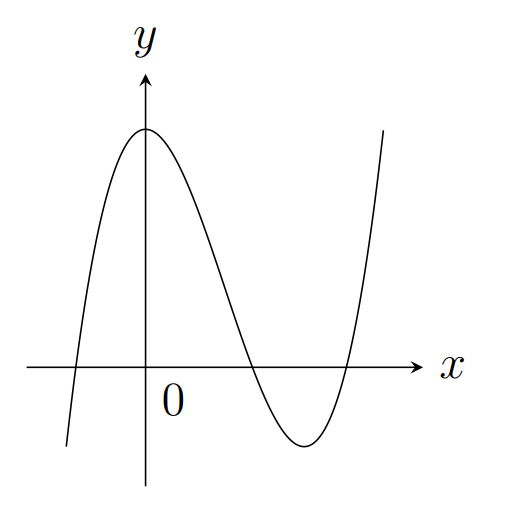
A. T = 6

B. T = 7

C. T = 9

D. T = 5

Câu 34:

Mô-đun của số phức z=(1+2i)(2-i) là

A. |z| = 5

B. |z| = $\sqrt{5}$

C. |z| = 10

D. |z| = 6

Câu 35:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,

\hat{A B C} = 60^{0},

cạnh bên

S A = \sqrt{2} a

và SA vuông góc với (ABCD). Tính góc giữa SB và (SAC).

A. $90^{0}$

B. $30^{0}$

C. $60^{0}$

D. $45^{0}$

Câu 36:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=AA'=a, AC=2a. Khoảng cách từ điểm D đến mặt phẳng (ACD') là

A. $\frac{a \sqrt{3}}{3} .$

B. $\frac{a \sqrt{5}}{5} .$

C. $\frac{a \sqrt{10}}{3} .$

D. $\frac{a \sqrt{21}}{7} .$

Câu 37:

Tìm độ dài đường kính của mặt cầu S có phương trình

x^{2} + y^{2} + z^{2} - 2 y + 4 z + 2 = 0.

A. $\sqrt{3}$

B. 2

C. 1

D. $2 \sqrt{3}$

Câu 38:

Cho đường thẳng $∆$ đi qua điểm M(2;0;-1) và có véc-tơ chỉ phương $\vec{a} = (4; - 6; 2) .$ Phương trình tham số của đường thẳng $∆$ là

A. $\{\begin{cases} x = 2 + 2 t \\ y = - 3 t \\ z = - 1 + t \end{cases}$

B. $\{\begin{cases} x = - 2 + 4 t \\ y = - 6 t \\ z = 1 + 2 t \end{cases}$

C. $\{\begin{cases} x = 4 + 2 t \\ y = - 6 - 3 t \\ z = 2 + t \end{cases}$

D. $\{\begin{cases} x = - 2 + 2 t \\ y = - 3 t \\ z = 1 + t \end{cases}$

Câu 39:

Giá trị lớn nhất của hàm số

y = 4 x^{2} + \frac{1}{x} - 2

trên đoạn [-1;2] bằng

A. $\frac{29}{2}$

B. 1

C. 3

D. Không tồn tại

Câu 40:

Bất phương trình $9^{x} - 2 (x + 5) 3^{x} + 9 (2 x + 1) \geq 0$ có tập nghiệm là $S = [a; b] \cup [c; + \infty) .$ Tính tổng a+b+c

A. 0

B. 1

C. 2

D. 3

Câu 41:

Giá trị của tích phân

I = \int_{0}^{1} \frac{x}{x + 1} d x

là

A. I = 2 + ln2

B. I = 1 + ln2

C. I = 1 - ln2

D. I = 2 - ln2

Câu 42:

Cho số phức

z = a + b i (a, b \in ℝ)

thỏa mãn phương trình

\frac{(|z| - 1) (1 + i z)}{z - \frac{1}{z}} = i .

Tính P=a+b

A. $P = 1 - \sqrt{2} .$

B. P=1.

C. $P = 1 + \sqrt{2} .$

D. P =0.

Câu 43:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A,

A C = a, \hat{A C B} = 60^{0} .

Đường chéo BC' của mặt bên (BCC'B') tạo với mặt phẳng ACC'A' một góc bằng

30 °

. Tính thể tích khối lăng trụ theo a.

A. $a^{3} \sqrt{3} .$

B. $a^{3} \sqrt{6} .$

C. $\frac{a^{3} \sqrt{3}}{3} .$

D. $\frac{a^{3} \sqrt{6}}{3} .$

Câu 44:

Mặt tiền của một ngôi biệt thự có 8 cây cột hình trụ tròn, tất cả đều có chiều cao bằng 4,2 m. Trong số các cây đó có 2 cây cột trước đại sảnh đường kính bằng 40 cm, 6 cây cột còn lại phân bố đều hai bên đại sảnh và chúng đều có đường kính bằng 26 cm. Chủ nhà thuê nhân công để sơn các cây cột bằng sơn giả đá biết giá thuê là 380000 đồng/1m2 (kể cả vật liệu sơn và nhân công thi công). Hỏi người chủ phải chi ít nhất bao nhiêu tiền để sơn hết các cây cột nhà đó (đơn vị đồng)? (lấy $π = 3,14159$ ).

A. $\approx$ 11.833.000

B. 12.521.000

C. $\approx$ 10.400.000

D. $\approx$ 15.642.000

Câu 45:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

d : \frac{x - 3}{1} = \frac{y - 3}{3} = \frac{z}{2}

và mặt phẳng (P): x+y-z+3=0. Đường thẳng

∆

đi qua A(1;2;-1), cắt d và song song với mặt phẳng (P) có phương trình là phương trình nào dưới đây?

A. $\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z + 1}{1} .$

B. $\frac{x - 1}{1} = \frac{y + 2}{2} = \frac{z + 1}{- 1} .$

C. $\frac{x - 1}{- 1} = \frac{y - 2}{- 2} = \frac{z + 1}{1} .$

D. $\frac{x - 1}{1} = \frac{y - 2}{- 2} = \frac{z + 1}{- 1} .$

Câu 46:

Cho hàm số y=f(x) liên tục trên R. Biết rằng đồ thị của hàm số y=f'(x) được cho bởi hình vẽ bên. Vậy khi đó hàm số

y = g (x) = f (x) - \frac{x^{2}}{2}

có bao nhiêu điểm cực đại?

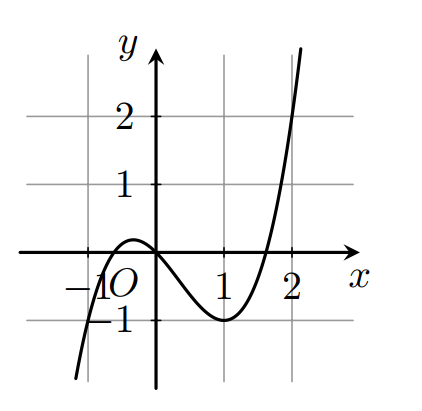
A. 3

B. 2

C. 0

D. 1

Câu 47:

Cho bất phương trình

\log_{3 a} 11 + \log_{\frac{1}{7}} (\sqrt{x^{2} + 3 a x + 10} + 4) . \log_{3 a} (x^{2} + 3 a x + 12) \geq 0.

Giá trị thực của tham số a để bất phương trình trên có nghiệm duy nhất thuộc khoảng nào sau?

A. (-1;0)

B. (1;2)

C. (0;1)

D. (2;-1)

Câu 48:

Cho parabol

(P) : y = x^{2} + 2

và hai tiếp tuyến của (P) tại các điểm M(-1;3) và N(2;6). Diện tích hình phẳng giới hạn bởi (P) và hai tiếp tuyến đó bằng

A. $\frac{9}{4}$

B. $\frac{13}{4}$

C. $\frac{7}{4}$

D. $\frac{21}{4}$

Câu 49:

Cho hai số phức

z_{1}, z_{2}

thỏa mãn

|z_{1} + 5| = 5, |z_{2} + 1 - 3 i| = |z_{2} - 3 - 6 i| .

Giá trị nhỏ nhất của

| z_{1} - z_{2} |

là

A. $\frac{5}{2}$

B. $\frac{7}{2}$

C. $\frac{1}{2}$

D. $\frac{3}{2}$

Câu 50:

Hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB=a,

\hat{A C B} = 30^{0}

và SA=SB=SD với S là trung điểm BC. Biết khoảng cách giữa hai đường thẳng SA và BC bằng

\frac{3 a}{4} .

Tính cos góc giữa hai mặt phẳng (SAC) và (SBC).

A. $\frac{2 \sqrt{5}}{11} .$

B. 3.

C. $\frac{\sqrt{65}}{13} .$

D. $\frac{\sqrt{5}}{33} .$

Đề số 25

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề số 25

CHỌN BỘ SÁCH BẠN MUỐN XEM