Đề số 25
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
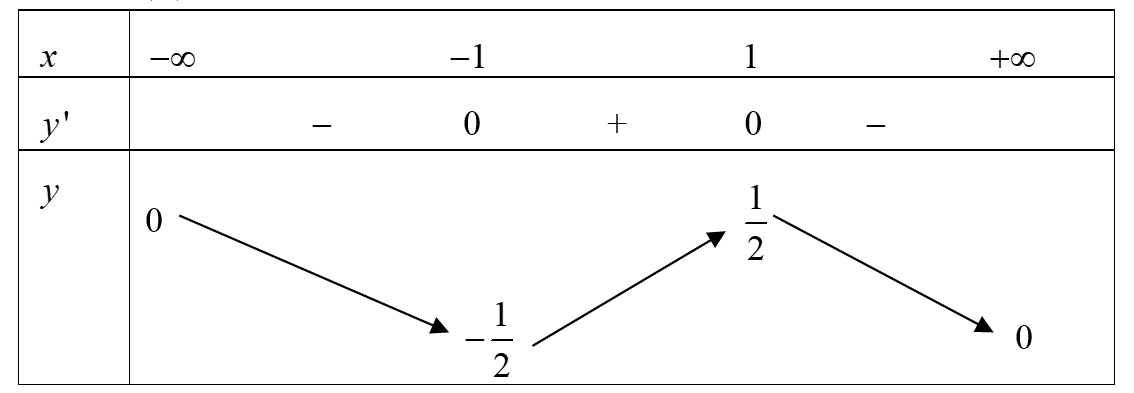
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là \(M,m.\) Giá trị biểu thức \(P = {M^2} + {m^2}\) bằng
A.\(P = \frac{1}{2}.\)
B.\(P = 1.\)
C.\(P = \frac{1}{4}.\)
D. \(P = 2.\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 2.\) Tính \({u_3}?\)
A.\({u_3} = 8.\)
B.\({u_3} = 4.\)
C.\({u_3} = 18.\)
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu như sau:
Hàm số \(y = f\left( x \right)\) đồng biến trong khoảng nào dưới đây?
A.\(\left( { - 2;0} \right).\)
B.\(\left( {0; + \infty } \right).\)
C.\(\left( { - \infty ; - 2} \right).\)
D. \(\left( { - 3;1} \right).\)
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và hai mặt bên \(\left( {SAB} \right),\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp \(S.ABC\) biết \(SC = a\sqrt 3 .\)
A.\(\frac{{2{a^3}\sqrt 6 }}{9}.\)
B.\(\frac{{{a^3}\sqrt 6 }}{{12}}.\)
C.\(\frac{{{a^3}\sqrt 3 }}{4}.\)
D. \(\frac{{{a^3}\sqrt 3 }}{2}.\)
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) là đúng?
A. Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
B. Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
C. Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
D. Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ.
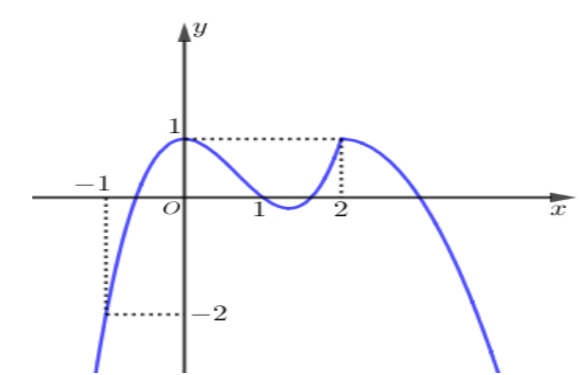
Hàm số \(g\left( x \right) = f\left( {{x^2}} \right) - \frac{{{x^6}}}{3} + {x^4} - {x^2}\) đạt cực tiểu tại bao nhiêu điểm?
A. 3.
B. 2.
C. 0.
D. 1.
Biết rằng đồ thị hàm số \(y = \frac{{\left( {m - 2n - 3} \right)x + 5}}{{x - m - n}}\) nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng \(S = {m^2} + {n^2} - 2.\)
A.\(S = 0.\)
B.\(S = 2.\)
C.\(S = - 1.\)
D. \(S = 1.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA\) vuông góc với đáy và \(SA = a\sqrt 3 .\) Góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
A.\({30^0}.\)
B.\({60^0}.\)
C.\(\arcsin \frac{3}{5}.\)
D.\({45^0}.\)
Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 8{x^2} + 16x - 9\) trên đoạn \(\left[ {1;3} \right]\) là
A.\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = 5.\)
B.\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 6.\)
C.\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = \frac{{13}}{{27}}.\)
D. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = 0.\)
Số đỉnh của hình mười hai mặt đều là:
A.Mười sáu.
B.Mười hai.
C.Ba mươi.
D.Hai mươi.
A.12.
B.10.
C.11.
D.20.
Đường cong sau đây là đồ thị của hàm số nào?
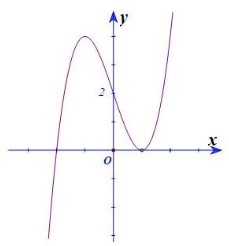
B.\(y = {x^3} - 3x + 2.\)
C.\(y = - {x^3} + 3x + 2.\)
D.\(y = {x^3} + 3x - 2.\)
Tìm hệ số \(h\) của số hạng chứa \({x^5}\) trong khai triển \({\left( {{x^2} + \frac{2}{x}} \right)^7}?\)
A.\(h = 84.\)
B. \(h = 560.\)
C.\(h = 672.\)
D. \(h = 280.\)
Gọi \(S\) là tập hợp các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;2} \right]\) bằng 2. Số phần tử của \(S\) là
A. 1.
B. 4.
C. 3.
D. 2.
Đồ thị hàm số \(y = \frac{{x + 1}}{{4x - 1}}\) có đường tiệm cận ngang là đường thẳng nào dưới đây?
A.\(x = - 1.\)
B.\(y = - 1.\)
C.\(y = \frac{1}{4}.\)
D. \(x = \frac{1}{4}.\)
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}.\)
A. 6.
B. 2.
C. 5.
D. 4.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 4;4} \right]\) và có bảng biến thiên trên đoạn \(\left[ { - 4;4} \right]\) như sau
![Cho hàm số y=f(x) liên tục trên đoạn [-4;4] và có bảng biến thiên trên đoạn [-4;4] như sau. Phát biểu nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1651165933/1651166122-image8.png)
Phát biểu nào sau đây đúng?
A. Hàm số không có GTLN, GTNN trên \(\left[ { - 4;4} \right].\)
B.\(\mathop {\min }\limits_{\left( { - 4;4} \right)} y = - 4\)và \(\mathop {\max }\limits_{\left( { - 4;4} \right)} y = 10.\)
C.\(\mathop {\max }\limits_{\left[ { - 4;4} \right]} y = 10\)và \(\mathop {\min }\limits_{\left[ { - 4;4} \right]} y = - 10.\)
D. \(\mathop {\max }\limits_{\left( { - 4;4} \right)} y = 0\)và \(\mathop {\min }\limits_{\left( { - 4;4} \right)} y = - 4.\)
Cho \(K\) là một khoảng, nửa khoảng hoặc một đoạn. Hàm số \(y = f\left( x \right)\) liên tục và xác định trên \(K.\) Mệnh đề nào không đúng?
A. Nếu hàm số \(y = f\left( x \right)\) đồng biến trên \(K\) thì \(f'\left( x \right) \ge 0,\forall x \in K.\)
B. Nếu \(f'\left( x \right) \ge 0,\forall x \in K\) thì hàm số \(y = f\left( x \right)\) đồng biến trên \(K.\)
C. Nếu hàm số \(y = f\left( x \right)\) là hàm số hằng trên \(K\) thì \(f'\left( x \right) = 0,\forall x \in K.\)
D. Nếu \(f'\left( x \right) = 0,\forall x \in K\) thì hàm số \(y = f\left( x \right)\) không đổi trên \(K.\)
Cho hai dãy ghế đối diện nhau mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
A.\(\frac{1}{{252}}.\)
B.\(\frac{1}{{945}}.\)
C.\(\frac{8}{{63}}.\)
D. \(\frac{4}{{63}}.\)
Bảng biến thiên trong hình vẽ là của hàm số
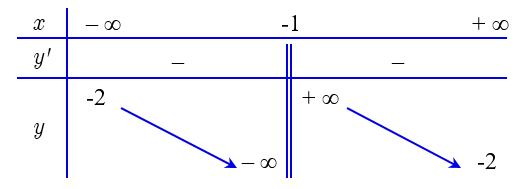
A. \(y = \frac{{ - 2x + 3}}{{x + 1}}.\)
B. \(y = \frac{{ - 2x - 4}}{{x + 1}}.\)
C. \(y = \frac{{2 - x}}{{x + 1}}.\)
D. \(y = \frac{{x - 4}}{{2x + 2}}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích \(V.\) Gọi \(E\) là điểm trên cạnh \(SC\) sao cho \(EC = 2ES.\) Gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng \(AE\) và song song với đường thẳng \(BD,\left( \alpha \right)\) cắt hai cạnh \(SB,SD\) lần lượt tại \(M,N.\) Tính theo \(V\) thể tích khối chóp \(S.AMEN.\)
A.\(\frac{V}{{12}}.\)
B.\(\frac{V}{{27}}.\)
C.\(\frac{V}{9}.\)
D. \(\frac{V}{6}.\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\},\) liên tục trên mỗi khoảng và có bảng biến thiên như sau:
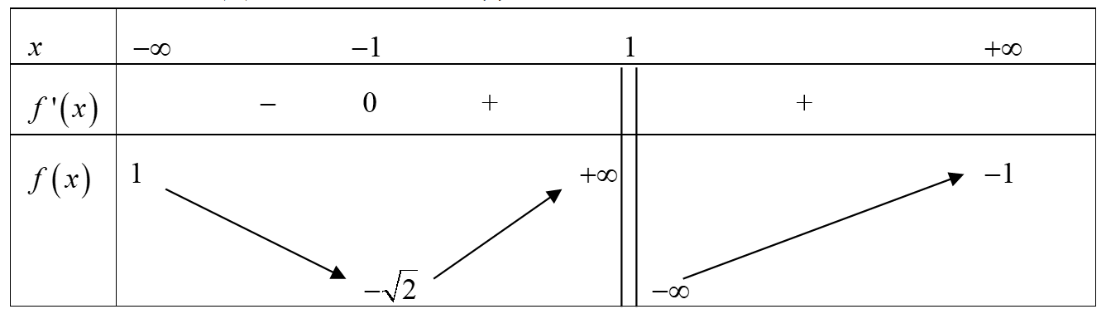
Tìm tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.
A.\(\left( { - 1;1} \right].\)
B.\(\left( { - \sqrt 2 ; - 1} \right).\)
C.\(\left( { - \sqrt 2 ; - 1} \right].\)
D. \(\left( { - 1;1} \right).\)
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = a,AD = 2a,SA\) vuông góc với mặt phẳng đáy và \(SA = a\sqrt 3 .\) Thể tích khối chóp \(S.ABCD\) bằng
A.\(2{a^3}\sqrt 3 .\)
B.\(\frac{{{a^3}\sqrt 3 }}{3}.\)
C.\(\frac{{2{a^3}\sqrt 3 }}{3}.\)
D. \({a^3}\sqrt 3 .\)
Cho tập \(A\) có 20 phần tử. Hỏi tập \(A\) có bao nhiêu tập con khác rỗng mà có số phần tử chẵn?
A.\({2^{20}}.\)
B. \({2^{19}} - 1.\)
C.\({2^{20}} + 1.\)
D.\({2^{19}}.\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Tìm số nghiệm thực phân biệt của phương trình \(f\left( x \right) = 1.\)
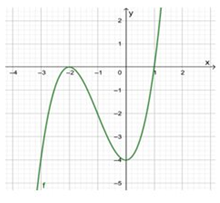
A. 0.
B. 2.
C. 1.
D. 3.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,SA \bot \left( {ABC} \right),\) góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}.\) Khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng:
A.\(\frac{{a\sqrt 3 }}{7}.\)
B.\(\frac{{a\sqrt 2 }}{2}.\)
C.\(\frac{{a\sqrt {15} }}{5}.\)
D. \(\frac{{a\sqrt 7 }}{7}.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm và liên tục trên \(\mathbb{R},\) có đồ thị như hình vẽ:
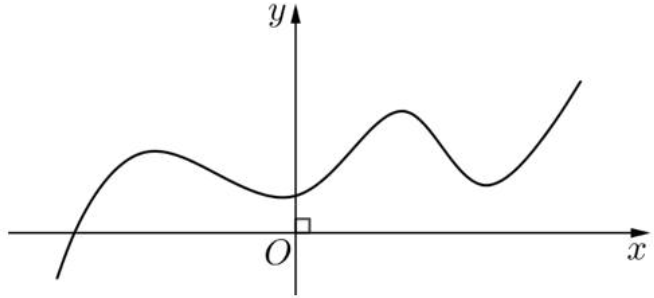
Số điểm cực trị của hàm số đã cho là:
A.3.
B.1.
C.4.
D.0.
Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc \(\left( C \right):y = {x^3} - 3{x^2} + 2,\) biết tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt \(\left( C \right)\) tại điểm \(N\left( {{x_N};{y_N}} \right)\) (khác \(M\)) sao cho \(P = 5x_M^2 + x_N^2\) đạt giá trị nhỏ nhất. Tính \(OM.\)
A.\(OM = \frac{{5\sqrt {10} }}{{27}}.\)
B.\(OM = \frac{{7\sqrt {10} }}{{27}}.\)
C.\(OM = \frac{{\sqrt {10} }}{{27}}.\)
D. \(OM = \frac{{10\sqrt {10} }}{{27}}.\)
Hàm số \(y = - {x^3} + 3{x^2} - 4\) đồng biến trên khoảng nào?
A.\(\left( { - \infty ;0} \right).\)
B.\(\left( {1;2} \right).\)
C.\(\left( {2; + \infty } \right).\)
D. \(\left( {0;3} \right).\)
Tìm \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x - 1}}.\)
A. 3.
B. 1.
C.\( - 1.\)
D. 2.
Cho khối chóp có thể tích \(V,\) diện tích đáy là \(B\) và chiều cao \(h.\) Tìm khẳng định đúng?
A.\(V = \frac{1}{3}Bh.\)
B.\(V = \sqrt {Bh} .\)
C.\(V = Bh.\)
D. \(V = 3Bh.\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên
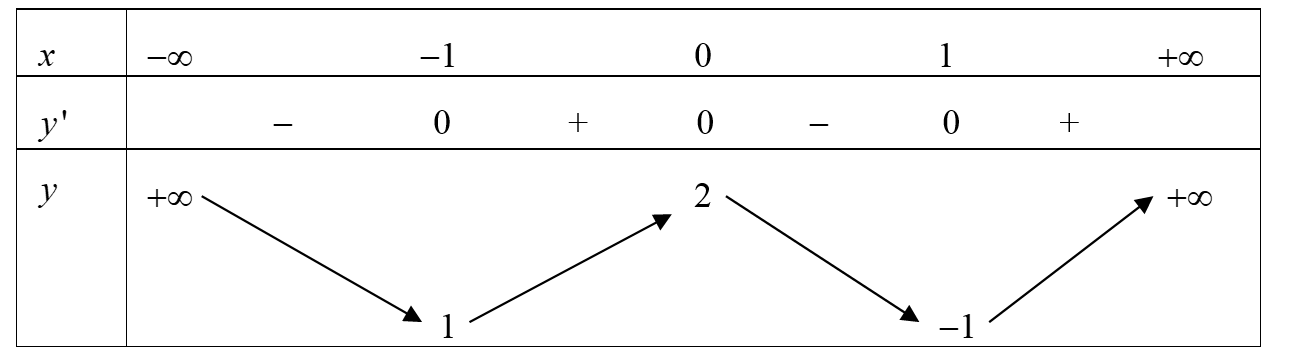
Khẳng định nào dưới đây sai?
A.\(f\left( { - 1} \right)\)là một giá trị cực tiểu của hàm số.
B.\({x_0} = 0\) là điểm cực đại của hàm số.
C.\({x_0} = 1\)là điểm cực tiểu của hàm số.
D. \(M\left( {0;2} \right)\)là điểm cực tiểu của đồ thị hàm số.
Tính thể tích khối tứ diện đều có cạnh bằng 2
A.\(\frac{{4\sqrt 2 }}{3}\)
C.\(\frac{{2\sqrt 2 }}{3}.\)
D.\(2\sqrt 3 .\)
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a.\) Gọi \(M,N\) lần lượt là trọng tâm các tam giác \(ABD,ABC\) và \(E\) là điểm đối xứng với \(B\) qua \(D.\) Mặt phẳng \(MNE\) chia khối tứ diện \(ABCD\) thành hai khối đa diện, trong đó khối đa diện chứa đỉnh \(A\) có thể tích \(V.\) Tính \(V.\)
A.\(V = \frac{{3\sqrt 2 {a^3}}}{{320}}.\)
B.\(V = \frac{{9\sqrt 2 {a^3}}}{{320}}.\)
C.\(V = \frac{{{a^3}\sqrt 2 }}{{96}}.\)
D. \(V = \frac{{3\sqrt 2 {a^3}}}{{80}}.\)
Cho \(k \in \mathbb{N},n \in \mathbb{N}.\) Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
A.\(C_{n + 1}^k = C_n^k + C_n^{k - 1}\)(với \(1 \le k \le n).\)
B.\(A_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)(với \(1 \le k \le n).\)
C.\(C_{n + 1}^k = C_n^{k + 1}\)(với \(1 \le k \le n).\)
D. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\)(với \(1 \le k \le n).\)
Cho hình chóp \(S.ABC\) có mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là điểm \(H\) nằm trong tam giác \(ABC\) sao cho \[\widehat {AHB} = {150^0},\widehat {BHC} = {120^0},\widehat {CHA} = {90^0}.\] Biết tổng diện tích các mặt cầu ngoại tiếp các hình chóp \(S.HAB,S.HBC,S.HCA\) là \(\frac{{124}}{3}\pi .\) Tính thể tích khối chóp \(S.ABC.\)
A.\(\frac{9}{2}.\)
B.\(\frac{4}{3}.\)
C.\(4{a^3}.\)
D.4.
Cho hàm số \(f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}.\) Đồ thị hàm số \(f'\left( x \right)\) như hình vẽ dưới đây
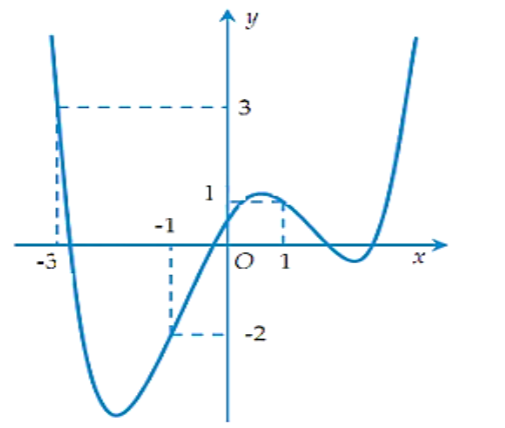
Xét hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{3}{x^3} - \frac{3}{4}{x^2} + \frac{3}{2}x + 2019.\) Trong các mệnh đề sau:
\(\left( I \right)g\left( 0 \right) < g\left( 1 \right).\)
\(\left( {II} \right)\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = g\left( { - 1} \right).\)
\(\left( {III} \right)\) Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - 3; - 1} \right).\)
\(\left( {IV} \right)\mathop {\max }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = \mathop {\max }\limits_{\left[ { - 3;1} \right]} \left\{ {g\left( { - 3} \right);g\left( 1 \right)} \right\}.\)
Số mệnh đề đúng là
A.2.
B.1.
C.3.
D.4.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Hai điểm \(M,N\) lần lượt thuộc các đoạn thẳng \(AB\) và \(AD(M\) và \(N\) không trùng với \(A)\) sao cho \(\frac{{AB}}{{AM}} + 2\frac{{AD}}{{AN}} = 4.\) Kí hiệu \(V,{V_1}\) lần lượt là thể tích của các khối chóp \(S.ABCD\) và \(S.MBCDN.\) Tìm giá trị lớn nhất của tỉ số \(\frac{{{V_1}}}{V}.\)
A.\(\frac{2}{3}.\)
B.\(\frac{1}{6}.\)
C.\(\frac{3}{4}.\)
D.\(\frac{{17}}{{14}}.\)
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới
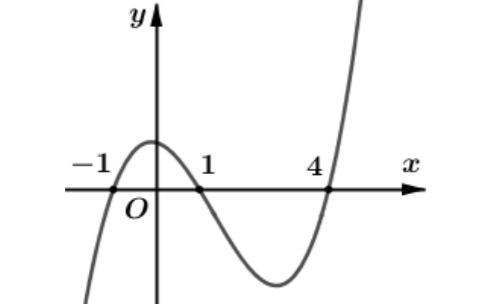
Hàm số \(g\left( x \right) = f\left( {\left| {3 - x} \right|} \right)\) đồng biến trên các khoảng nào trong các khoảng sau?
A.\(\left( {4;7} \right).\)
B.\(\left( { - 1;2} \right).\)
C.\(\left( {2;3} \right).\)
D.\(\left( { - \infty ; - 1} \right).\)
Cho tứ diện \(SABC\) có các cạnh \(SA,SB,SC\) đôi một vuông góc với nhau. Biết \(SA = 3a,SB = 4a,SC = 5a.\) Tính theo \(a\) thể tích \(V\) của khối tứ diện \(SABC\).
A.\(V = 20{a^3}.\)
B.\(V = 10{a^3}.\)
C.\(V = \frac{{5{a^3}}}{2}.\)
D. \(V = 5{a^3}.\)
A.\(y = {x^2}.\)
B. \(y = 2x.\)
C.\(y = \frac{{x - 1}}{x}.\)
D.\(y = 0.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}.\) Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới
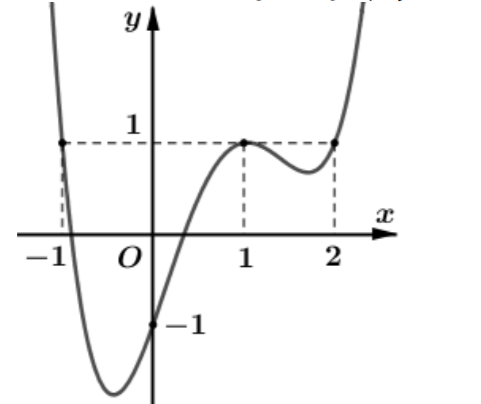
Đặt \(g\left( x \right) = f\left( x \right) - x,\) khẳng định nào sau đây là đúng?
B.\(g\left( { - 1} \right) < g\left( 1 \right) < g\left( 2 \right).\)
C.\(g\left( 2 \right) < g\left( { - 1} \right) < g\left( 1 \right).\)
D.\(g\left( 1 \right) < g\left( { - 1} \right) < g\left( 2 \right).\)
Viết phương trình tiếp tuyến với đồ thị \(\left( C \right):y = {x^3} - 3{x^2}\) tại điểm \(M\left( {1; - 2} \right).\)
A.\(y = - 3x + 1.\)
B. \(y = - 3x - 1.\)
C.\(y = 3x - 5.\)
D. \(y = - 2.\)
Cho phương trình: \({\sin ^3}x + 2\sin x + 3 = \left( {2{{\cos }^3}x + m} \right)\sqrt {2{{\cos }^3}x + m - 2} + 2{\cos ^3}x + {\cos ^2}x + m.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình trên có đúng một nghiệm \(x \in \left[ {0;\frac{{2\pi }}{3}} \right)?\)
A. 4.
B. 3.
C. 2.
D. 1.
Cho một tấm nhôm hình vuông cạnh \(6\left( {cm} \right).\) Người ta muốn cắt một hình thang như hình vẽ.
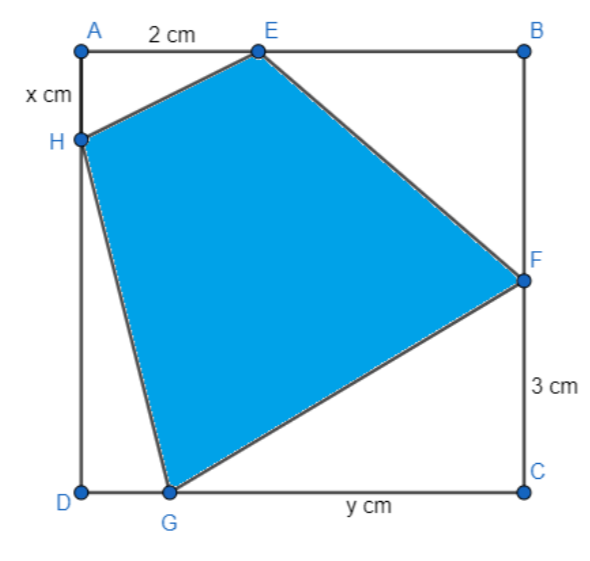
Trong đó \(AE = 2\left( {cm} \right),AH = x\left( {cm} \right),CF = 3\left( {cm} \right),CG = y\left( {cm} \right).\) Tìm tổng \(x + y\) để diện tích hình thang \(EFGH\) đạt giá trị nhỏ nhất.
A.\(x + y = 7.\)
B. \(x + y = 5.\)
C.\(x + y = \frac{{7\sqrt 2 }}{2}.\)
D. \(x + y = 4\sqrt 2 .\)
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 ,\) cạnh bên bằng \(2a.\) Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SCD} \right).\) Tính \(\cos \alpha .\)
A.\(\frac{{\sqrt {21} }}{2}.\)
B.\(\frac{{\sqrt {21} }}{{14}}.\)
C.\(\frac{{\sqrt {21} }}{3}.\)
D. \(\frac{{\sqrt {21} }}{7}.\)
Cho hàm số \(y = - {x^4} + 2{x^2}\) có đồ thị như hình vẽ.
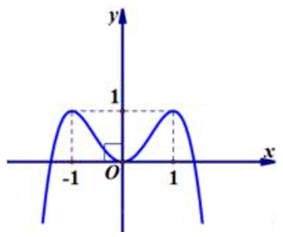
Tìm tất cả các giá trị thực của \(m\) để phương trình \( - {x^4} + 2{x^2} = m\) có hai nghiệm phân biệt.
A.\(m = 1\)hoặc \(m < 0.\)
B.\(0 < m < 1.\)
C.\(m < 1.\)
D. \(m >0.\)
Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 6\) có hai điểm cực trị
A. 1.
B.4.
C. vô số.
Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) có hai tiệm cận đứng?
A. 2.
B. 3.
C. 1.
D. 0.
Cho khối đa diện đều giới hạn bởi hình đa diện \(\left( H \right),\) khẳng định nào sau đây là sai?
A. Các mặt của \(\left( H \right)\) là những đa giác đều có cùng số cạnh.
B. Mỗi cạnh của một đa giác của \(\left( H \right)\) là cạnh chung của nhiều hơn hai đa giác.
C. Khối đa diện đều \(\left( H \right)\) là một khối đa diện lồi.
D. Mỗi đỉnh của \(\left( H \right)\) là đỉnh chung của cùng một số cạnh.