Đề số 26

Câu 1:

Từ các chữ số 1;2;3;4;5;6;7;8;9 có thể lập được bao nhiêu số tự nhiên có hai chữ số khác nhau?

A. $A_{9}^{2}$

B. $C_{9}^{2}$

C. 2⁹

D. 9²

Câu 2:

Cho cấp số cộng (u_n) với u₁=2 và công sai d=1. Khi đó

u₃bằng

A. 3

B. 1

C. 4

D. 2

Câu 3:

Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây. Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?

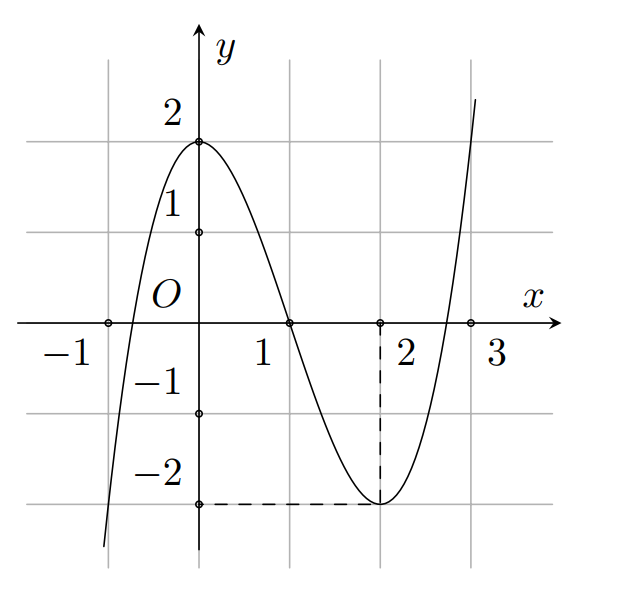
A. (-1;2)

B. (0;2)

C. $(- \infty; 0)$

D. $(2; + \infty)$

Câu 4:

Cho hàm số y=f(x) có đạo hàm trên R và có bảng xét dấu y' như sau

Media VietJack

Hàm số y=f(x) đạt cực đại tại điểm

A. x = 2

B. x = 2 và x = -2

C. x = -2

D. x = 0

Câu 5:

Cho hàm số có đồ thị y=f(x) như hình vẽ bên dưới. Trên đoạn [-3;1] hàm số đã cho có mấy điểm cực trị?

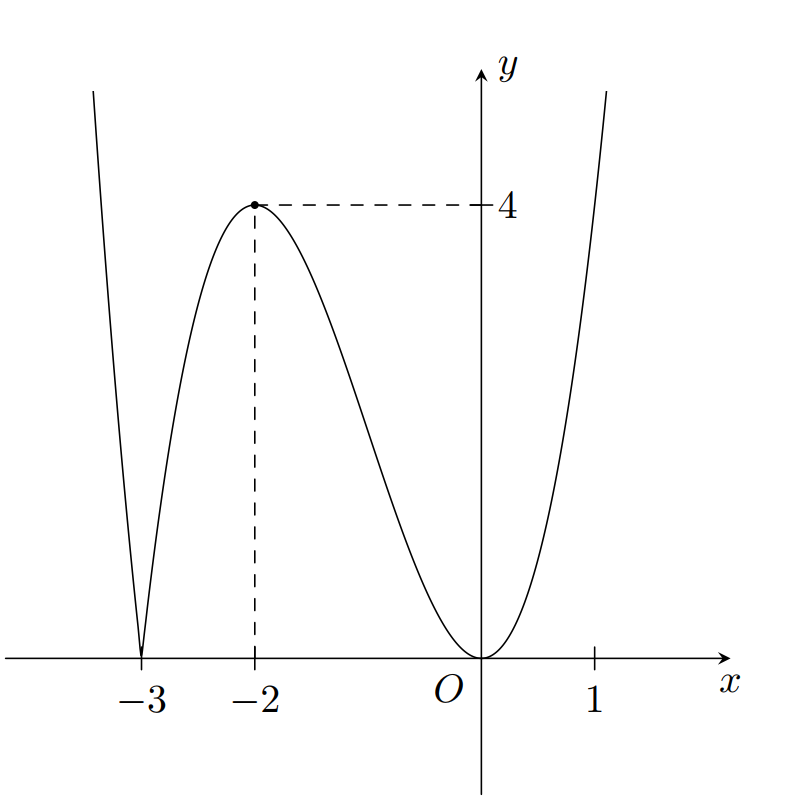
A. 1

B. 2

C. 3

D. 4

Câu 6:

Cho hàm số

y = \frac{2}{x - 5} .

Tìm đường tiệm cận ngang của đồ thị hàm số.

A. $y = - \frac{2}{5} .$

B. y = 2.

C. y = 0.

D. x = 5.

Câu 7:

Đường cong hình bên là đồ thị của hàm số

y = a x^{4} + b x^{2} + c

với a,b,c là các số thực. Mệnh đề nào dưới đây đúng?

A. $a < 0; b > 0; c < 0.$

B. $a > 0; b > 0; c < 0.$

C. $a > 0; b < 0; c < 0$

D. $a < 0; b < 0; c > 0$

Câu 8:

Cho hàm số

y = (x - 2) (x^{2} + 1)

có đồ thị (C) Mệnh đề nào sau đây đúng?

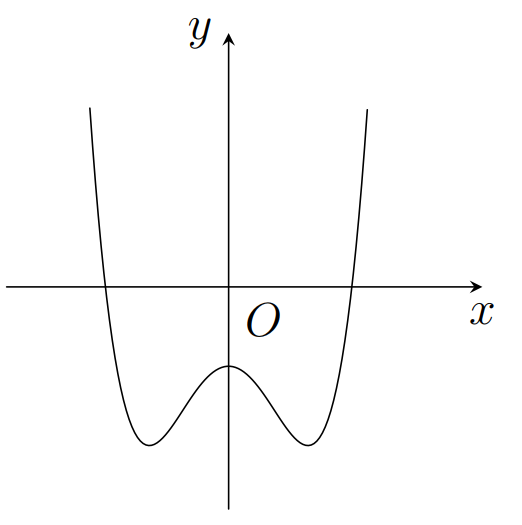
A. (C) cắt trục hoành tại hai điểm.

B. (C) cắt trục hoành tại một điểm.

C. (C) không cắt trục hoành.

D. (C) cắt trục hoành tại ba điểm.

Câu 9:

Với các số thực dương a,b bất kì. Mệnh đề nào dưới đây đúng?

A. $\ln (a b) = \ln a + \ln b .$

B. $\ln (a b) = \ln a . \ln b .$

C. $\ln \frac{a}{b} = \frac{\ln a}{\ln b} .$

D. $\ln \frac{a}{b} = \ln b - \ln a .$

Câu 10:

Đạo hàm của hàm số $y = 3^{x}$ là

A. $y' = 3^{x} \ln 3.$

B. $y' = \frac{3^{x}}{\ln 3} .$

C. $y' = x 3^{x - 1} .$

D. $y' = 3^{x} .$

Câu 11:

Cho các số thực m,n và a là số thực dương. Mệnh đề nào sau đây là mệnh đề đúng?

A. $a^{m + n} = {(a^{m})}^{n} .$

B. $a^{m + n} = \frac{a^{m}}{a^{n}}$ .

C. $a^{m + n} = a^{m} . a^{n} .$

D. $a^{m + n} = a^{m} + n .$

Câu 12:

Tìm tập nghiệm S của phương trình

3^{x^{2}} = 9.

A. $S = \{\sqrt{2}; 2\}$ .

B. $S = \{- \sqrt{2}; \sqrt{2}\}$ .

C. $S = \{- \sqrt{2}; 2\}$ .

D. $S = \{- 2; 2\} .$

Câu 13:

Phương trình

\log_{2} (x - 3) = 3

có nghiệm là

A. x = 5

B. x = 12

C. x = 9

D. x = 11

Câu 14:

Tìm nguyên hàm của hàm số

f (x) = 2 x^{3} - 9.

A. $\int_{}^{} f (x) d x = \frac{1}{2} x^{4} - 9 x + C .$

B. $\int_{}^{} f (x) d x = x^{4} - 9 x + C .$

C. $\int_{}^{} f (x) d x = \frac{1}{2} x^{4} + C .$

D. $\int_{}^{} f (x) d x = 4 x^{3} + 9 x + C .$

Câu 15:

Họ nguyên hàm của hàm số

f (x) = e^{2 x} + x^{2}

là

A. $F (x) = \frac{e^{2 x}}{2} + \frac{x^{3}}{3} + C .$

B. $F (x) = e^{2 x} + x^{3} + C .$

C. $F (x) = 2 e^{2 x} + 2 x + C .$

D. $F (x) = e^{2 x} + \frac{x^{3}}{3} + C .$

Câu 16:

Biết

\int_{a}^{b} f (x) d x = 10, F (x)

là một nguyên hàm của f(x) và F(a)=-3. Tính F(b)

A. F(b) = 13.

B. F(b) = 10.

C. F(b) = 16.

D. F(b) = 7.

Câu 17:

Cho

\int_{2}^{5} f (x) d x = 10.

Khi đó

\int_{5}^{2} [2 - 4 f (x)] d x

bằng

A. 32

B. 34

C. 42

D. 46

Câu 18:

Cho số phức

z = 7 - i \sqrt{5}

. Phần thực và phần ảo của số phức

\bar{z}

lần lượt là

A. 7 và $\sqrt{5}$

B. -7 và $\sqrt{5}$

C. 7 và $i \sqrt{5}$

D. 7 và $- \sqrt{5}$

Câu 19:

Cho hai số phức

z_{1} = 2 - 2 i, z_{2} = - 3 + 3 i .

Khi đó số phức

z_{1} - z_{2}

là

A. -5 + 5i

B. -5i

C. 5 - 5i

D. -1 + i

Câu 20:

Trên mặt phẳng tọa độ Oxyz cho điểm M trong hình vẽ bên là điểm biễu diễn của số phức z. Tìm z

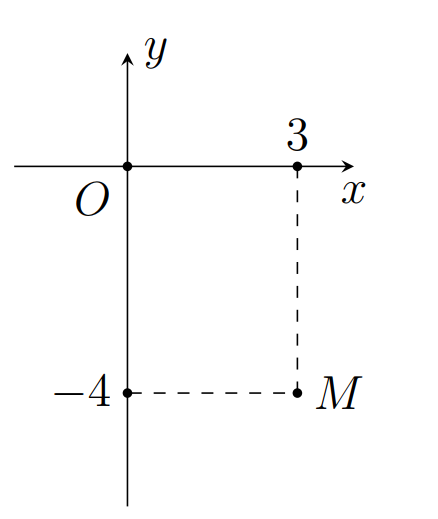
A. z = -4 + 3i

B. z = -3 + 4i

C. z = 3 - 4i

D. z = 3 + 4i

Câu 21:

Tính thể tích V của khối hộp có chiều cao bằng h và diện tích đáy bằng B.

A. $V = \frac{1}{3} B . h$

B. V = B.h

C. $V = \frac{1}{2} B . h$

D. $V = \frac{1}{6} B . h$

Câu 22:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có

A B = 2 a, A A' = a \sqrt{3} .

Tính thể tích khối lăng trụ ABC.A'B'C'.

A. $3 a^{3} .$

B. $a^{3} .$

C. $\frac{a^{3}}{4} .$

D. $\frac{3 a^{3}}{4} .$

Câu 23:

Một khối trụ có bán kính đáy R đường cao h. Thể tích khối trụ bằng

A. $V = π R^{2} h$

B. $\frac{1}{3} π R^{2} h .$

C. $2 π R^{2} h .$

D. $2 π R h .$

Câu 24:

Cho tam giác SOA vuông tại O có

S O = 3 c m, S A = 5 c m .

Quay tam giác SOA xung quanh cạnh SO được khối nón. Thể tích khối nón tương ứng là

A. $16 π c m^{3} .$

B. $36 π c m^{3} .$

C. $15 π c m^{3} .$

D. $\frac{80 π}{3} π c m^{3} .$

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $M (- 1; 2; 3), N (0; 2; - 1) .$ Tọa độ trọng tâm của tam giác OMN là

A. $(- \frac{1}{3}; \frac{4}{3}; \frac{2}{3}) .$

B. $(- \frac{1}{2}; 2; 1) .$

C. (1;0;-4).

D. (-1;4;2).

Câu 26:

Viết phương trình mặt cầu tâm I(1;-2;3) và bán kính R=2.

A. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 4.$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 4.$

C. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 2 .$

D. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 2 .$

Câu 27:

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A (1; 0; 0), B (0; - 2; 0), C (0; 0; 3) .$ Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?

A. $\frac{x}{3} + \frac{y}{1} + \frac{z}{- 2} = 1.$

B. $\frac{x}{1} + \frac{y}{- 2} + \frac{z}{3} = 0.$

C. $\frac{x}{- 2} + \frac{y}{1} + \frac{z}{3} = 1.$

D. $\frac{x}{1} + \frac{y}{- 2} + \frac{z}{3} = 1$ .

Câu 28:

Trong không gian Oxyz, cho hai điểm A(2;-1;4) và B(-1;3;2). Đường thẳng AB có một véc-tơ chỉ phương là

A. $\vec{m} (1; - 4; 2) .$

B. $\vec{u} (1; 2; 2)$ .

C. $\vec{v} (- 3; 4; - 2) .$

D. $\vec{n} (1; 2; 6)$ .

Câu 29:

Có 16 tấm bìa ghi 16 chữ “HỌC”, “ĐỂ”, “BIẾT”, “HỌC”, “ĐỂ”, “LÀM”, “HỌC”, “ĐỂ”, “CHUNG”, “SỐNG”, “HỌC”, “ĐỀ”, “TỰ”, “KHẲNG”, “ĐỊNH”, “MÌNH”. Một người xếp ngẫu nhiên 16 tấm bìa cạnh nhau. Tính xác suất để xếp các tấm bìa được dòng chữ “HỌC ĐỀ BIẾT HỌC ĐỂ LÀM HỌC ĐỂ CHUNG SỐNG HỌC ĐỂ TỰ KHẲNG ĐỊNH MÌNH

A. $\frac{8}{16!}$

B. $\frac{4!}{16!}$

C. $\frac{1}{16!}$

D. $\frac{4! .4!}{16!}$

Câu 30:

Cho hàm số y=f(x) có đồ thị như hình bên. Khi đó y=f(x) là hàm số nào sau đây?

A. $y = x^{3} - 3 x .$

B. $y = - x^{3} + 3 x$

C. $y = x^{3} + x^{2} - 4.$

D. $y = x^{3} - 3 x + 1.$

Câu 31:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;1].

A. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = 1.$

B. $\max_{[0; 1]} y = 0, \min_{[0; 1]} y = - 2.$

C. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = - 2.$

D. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = 0.$

Câu 32:

Tập nghiệm của bất phương trình

3^{x} > 9

là

A. $(2; + \infty)$

B. (0;2)

C. $(0; + \infty)$

D. $(- 2; + \infty)$

Câu 33:

Tính tích phân

I = \int_{0}^{\frac{π}{4}} \cos (\frac{π}{2} - x) d x .

A. $I = \frac{1 - \sqrt{2}}{\sqrt{2}}$ .

B. $I = 1 - \sqrt{2} .$

C. $I = \frac{\sqrt{2} - 1}{\sqrt{2}} .$

D. $I = \sqrt{2} - 1.$

Câu 34:

Cho hai số phức

z_{1} = 1 + 2 i v à z_{2} = 2 - 3 i .

Phần ảo của số phức

w = 3 z_{1} - 2 z_{2}

là

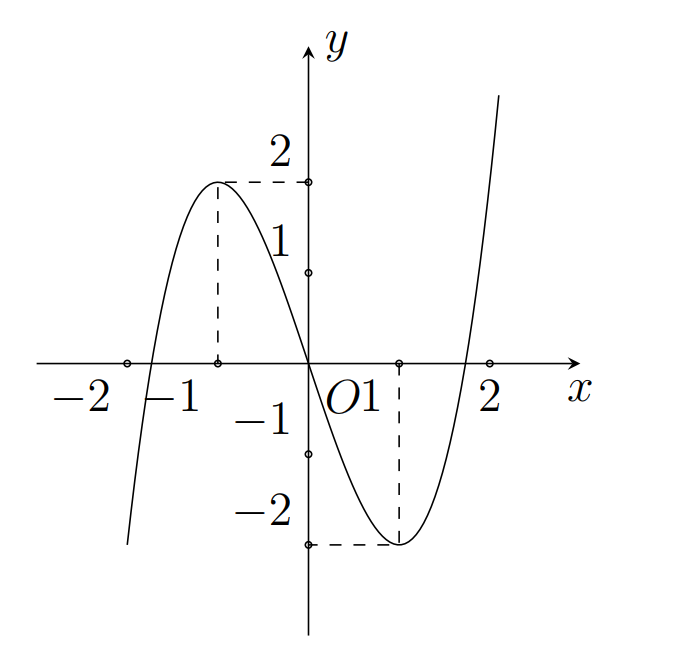
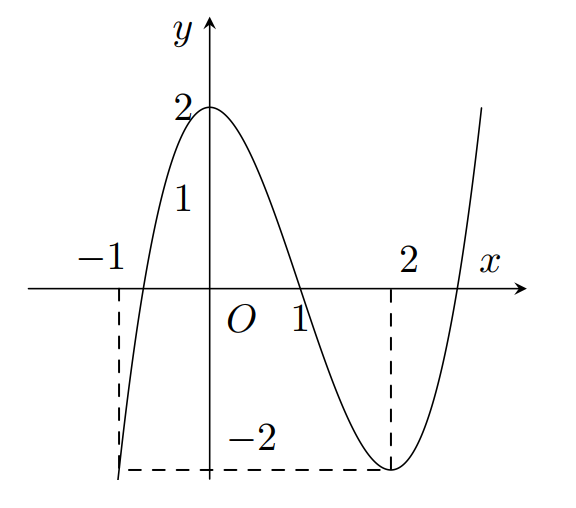
A. 12

B. 1

C. 11

D. 12i

Câu 35:

Cho hình chóp S.ABC có SA vuông góc với đáy ABC. Tam giác ABC vuông cân tại B và

S A = a \sqrt{2}, S B = a \sqrt{5} .

Tính góc giữa SC và mặt phẳng (ABC).

A. $45^{0}$

B. $30^{0}$

C. $120^{0}$

D. $60^{0}$

Câu 36:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh

a, S A ⊥ (A B C D)

và SA=a. Khoảng cách từ điểm A đến mặt phẳng (SBD) bằng

A. $\frac{a}{2} .$

B. $\frac{a \sqrt{6}}{3} .$

C. $\frac{a \sqrt{3}}{3} .$

D. $\frac{a \sqrt{2}}{2} .$

Câu 37:

Trong không gian Oxyz cho mặt cầu (S) có tâm I(1;1;1). Một mặt phẳng (P) cắt (S) theo giao tuyến là một đường tròn (C). Biết chu vi lớn nhất của (C) bằng $2 π \sqrt{2} .$ Phương trình của (S) là

A. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 4 .$

B. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 2$ .

C. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 4 .$

D. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 2.$

Câu 38:

Trong không gian Oxyz, cho A(1;-2;1) và B(0;1;3) Phương trình đường thẳng đi qua hai điểm A,B là

A. $\frac{x + 1}{- 1} = \frac{y - 3}{- 2} = \frac{z - 2}{1} .$

B. $\frac{x}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{2} .$

C. $\frac{x + 1}{- 1} = \frac{y - 2}{3} = \frac{z + 1}{2} .$

D. $\frac{x}{1} = \frac{y - 1}{- 2} = \frac{z - 3}{1} .$

Câu 39:

Tìm tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số

y = |x^{2} + 2 x + m - 4|

trên đoạn [-2;1] đạt giá trị nhỏ nhất. Giá trị của m là

A. 5

B. 4

C. 1

D. 3

Câu 40:

Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện

3^{|x^{2} - 2 x - 3| - \log_{3} 5} = 5^{- (y + 4)} và 4 |y| - |y - 1| + {(y + 3)}^{2} \leq 8.

A. 3

B. 2

C. 1

D. 4

Câu 41:

Biết $\int_{0}^{1} \frac{x^{3} + 3 x}{x^{2} + 3 x + 2} d x = a + b \ln 2 + c \ln 3$ với a,b,c là các số hữu tỉ, tính $S = 2 a + b^{2} + c^{2} .$

A. S = 515

B. S = 164

C. S = 436

D. S = -9

Câu 42:

Cho số phức

z = a + b i (a, b \in ℝ, a < 0)

thỏa mãn

1 + \bar{z} = {|\bar{z} - i|}^{2} + {(i z - 1)}^{2} .

Tính |z|

A. $\frac{\sqrt{2}}{2} .$

B. $\sqrt{5} .$

C. $\frac{\sqrt{17}}{2} .$

D. $\frac{1}{2} .$

Câu 43:

Cho hình hình hộp chữ nhật ABCD.A'B'C'D'có đáy là hình vuông cạnh a chiều cao

A A' = a \sqrt{3} .

Gọi M là trung điểm của CC'. Tính thể tích của khối tứ diện BDA'M

A. $\frac{a^{3} \sqrt{3}}{6} .$

B. $\frac{a^{3} \sqrt{3}}{4} .$

C. $\frac{a^{3} \sqrt{3}}{15} .$

D. $\frac{a^{3} \sqrt{3}}{12} .$

Câu 44:

Một chiếc cốc hình trụ có đường kính đáy 6 cm, chiều cao 15 cm chứa đầy nước. Nghiêng cốc cho nước chảy từ từ ra ngoài cho đến khi mép nước ngang với đường kính của đáy. Khi đó diện tích của bề mặt nước trong cốc bằng.

A. $9 \sqrt{26 π} c m^{2} .$

B. $\frac{9 \sqrt{26} π}{2} c m^{2} .$

C. $\frac{9 \sqrt{26} π}{5} c m^{2} .$

D. $\frac{9 \sqrt{26} π}{10} c m^{2} .$

Câu 45:

Trong không gian Oxyz, cho đường thẳng

d : \{\begin{cases} x = 1 + 2 t \\ y = - t \\ z = 2 + t \end{cases}

và mặt phẳng (P): x+2y+1=0. Tìm hình chiếu của đường thẳng d trên (P)

A. $\{\begin{cases} x = \frac{19}{5} + 2 t \\ y = - \frac{2}{5} - t \\ z = t \end{cases} .$

B. $\{\begin{cases} x = \frac{19}{5} + 2 t \\ y = - \frac{12}{5} - t \\ z = 1 + t \end{cases} .$

C. $\{\begin{cases} x = \frac{3}{5} + 2 t \\ y = - \frac{4}{5} - t \\ z = 2 + t \end{cases} .$

D. $\{\begin{cases} x = \frac{1}{5} + 2 t \\ y = - \frac{2}{5} - t \\ z = 1 + t \end{cases} .$

Câu 46:

Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ bên. Số điểm cực trị của hàm số

g (x) = 3 f (x) + x^{3} - 15 x + 1

là

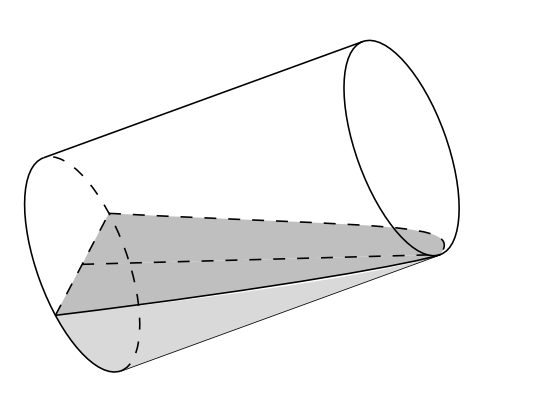
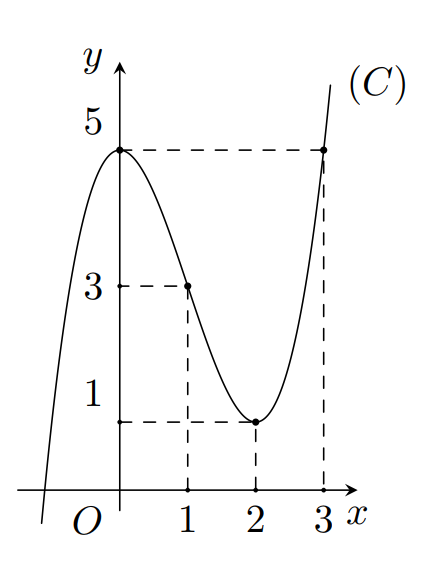
A. 2

B. 1

C. 3

D. 4

Câu 47:

Giả sử S=(a;b] là tập nghiệm của bất phương trình $5 x + \sqrt{6 x^{2} + x^{3} - x^{4}} \log_{2} x > (x^{2} - x) \log_{2} x + 5 + 5 \sqrt{6 + x - x^{2}} .$

Khi đó b-a bằng

A. $\frac{1}{2}$

B. 2

C. $\frac{7}{2}$

D. $\frac{5}{2}$

Câu 48:

Cho (H) là hình phẳng giới hạn bởi parabol $y = \sqrt{3} x^{2}$ và nửa đường tròn có phương trình $y = \sqrt{4 - x^{2}} với - 2 \leq x \leq 2$ (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

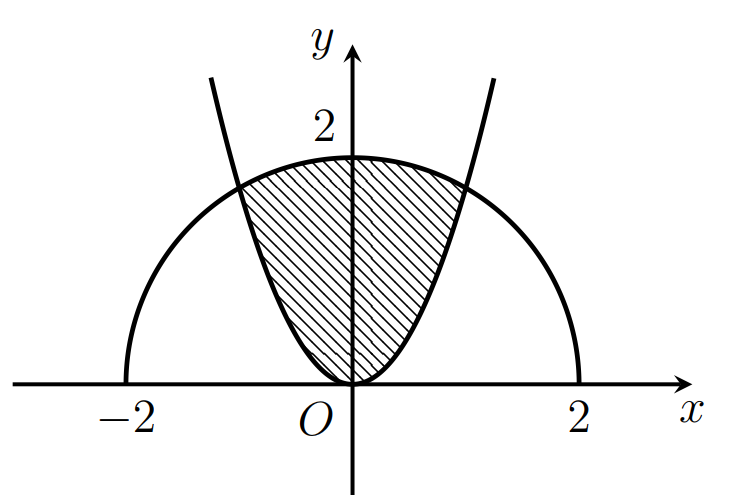
Media VietJack

A. $\frac{2 π + 5 \sqrt{3}}{3} .$

B. $\frac{4 π + 5 \sqrt{3}}{3} .$

C. $\frac{4 π + \sqrt{3}}{3} .$

D. $\frac{2 π + \sqrt{3}}{3} .$

Câu 49:

Cho số phức z thỏa mãn điều kiện $|z + 2| = |z + 2 i| .$ Giá trị nhỏ nhất của biểu thức $P = |z - 1 - 2 i| + |z - 3 - 4 i| + |z - 5 - 6 i|$ được viết dưới dạng $(a + b \sqrt{17}) / \sqrt{2}$ với a,b là các hữu tỉ. Giá trị của a+b là

A. 3

B. 2

C. 7

D. 4

Câu 50:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của BC và H là trung điểm của AM. Biết $H B = H C, \hat{H B C} = 30^{0};$ góc giữa mặt phẳng (SHC) và mặt phẳng (HBC) bằng $60^{0} .$ Tính cô-sin của góc giữa đường thẳng BC và mặt phẳng (SHC).

A. $\frac{1}{2}$

B. $\frac{\sqrt{3}}{2}$

C. $\frac{\sqrt{13}}{4}$

D. $\frac{\sqrt{3}}{4}$

Đề số 26

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề số 26

CHỌN BỘ SÁCH BẠN MUỐN XEM