Đề số 6

Câu 1:

Cho hình nón có bán kính đường tròn đáy là 6cm và diện tích hình tròn đáy bằng $\frac{3}{5}$ diện tích xung quanh của hình nón. Tính thể tích V khối nón

A. $V = 120 π ({cm}^{3})$

B. $V = 64 π ({cm}^{3})$

C. $V = 96 π ({cm}^{3})$

D. $V = 288 π ({cm}^{3})$

Câu 2:

Tìm cực tiểu của hàm số $y = - x^{3} + 6 x^{2} + 15 x + 10$

A. 5

B. 110

C. 2

D. -1

Câu 3:

Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?

A. $y = \frac{2 x - 3}{3 x - 1}$

B. $y = \frac{- 2 x + 3}{x + 1}$

C. $y = \frac{3 x + 4}{x - 1}$

D. $y = \frac{4 x + 1}{x + 2}$

Câu 4:

Tính thể tích V của khối lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2a

A. $V = \frac{a^{3} \sqrt{3}}{2}$

B. $V = \frac{a^{3} \sqrt{3}}{6}$

C. $V = \frac{2 a^{3} \sqrt{3}}{3}$

D. $V = 2 a^{3} \sqrt{3}$

Câu 5:

Kí hiệu (H) là hình phẳng giới hạn bởi đường cong y =tan x trục hoành và hai đường thẳng x = 0; x = $\frac{π}{4}$ . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox

A. $V = - π (1 - \frac{π}{4})$

B. $V = (1 + \frac{π}{4})$

C. $V = π (1 - \frac{π}{4})$

D. $V = π (2 - \frac{π}{4})$

Câu 6:

Trong không gian với hệ trục tọa độ Oxyz, cho A(1;2;-5), B(-3;0;1). Viết phương trình mặt cầu (S) có đường kính là AB.

A. $(S) : {(x + 2)}^{2} + {(y + 1)}^{2} + {(z - 3)}^{2} = 14$

B. $(S) : {(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 56$

C. $(S) : {(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 14$

D. $(S) : {(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 56$

Câu 7:

Cho số phức z thỏa mãn $\frac{30 i}{1 - z} = 9 - 3 i$ . Gọi M là điểm biểu diễn số phức z. Tìm tung độ của M

A. 2

B. 3

C. -3

D. -1

Câu 8:

Trong không gian với hệ trục tọa độ Oxyz, gọi H là hình chiếu vuông góc của điểm A(-3;-1;-1) lên mặt phẳng (P): 2x + y + z - 4 = 0. Tìm tọa độ điểm H

A. H(2;0;0)

B. H(1;2;0)

C. H(1;1;1)

D. $H (\frac{1}{2}; 1; 2)$

Câu 9:

Cho hai điểm A(0;-1;2), B(4;1;-1) và mặt phẳng $(α) : 3 x - y + z - 2 = 0$ . Xét vị trí tương đối của hai điểm AB, và $(α)$ .

A. $A \notin (α), B \in (α)$

B. $A \in (α), B \notin (α)$

C. A, B nằm về một phía đối với $(α)$

D. A, B nằm về hai phía đối với $(α)$

Câu 10:

Cho f(x) là hàm số chẵn trên $ℝ$ thỏa mãn $\int_{- 3}^{0} f (x) d x = 2$ . Chọn mệnh đề đúng.

A. $\int_{- 3}^{3} f (x) d x = 2$

B. $\int_{- 3}^{3} f (x) d x = 4$

C. $\int_{0}^{3} f (x) d x = - 2$

D. $\int_{0}^{3} f (x) d x = - \int_{- 3}^{0} f (x) d x$

Câu 11:

Hàm số nào sau đây thỏa mãn với mọi $x_{1}, x_{2} \in ℝ, x_{1} > x_{2}$ thì $f (x_{1}) > f (x_{2})$ ?

A. $f (x) = x^{4} + 2 x^{2} + 1$

B. $f (x) = \frac{2 x + 1}{x + 3}$

C. $f (x) = x^{3} + x^{2} + 1$

D. $f (x) = x^{3} + x^{2} + 3 x + 1$

Câu 12:

Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện $|z - (1 + i)| = |z + 2 i|$ là đường nào trong các đường cho dưới đây?

A. Đường thẳng

B. Đường tròn

C. Elip

D. Parabo

Câu 13:

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số $y = f (x) = \sqrt{x} e^{x^{2}}$ , trục hoành, đường thẳng x = 1. Tính thể tích V của khối tròn xoay thu được khi (H) quay quanh trục hoành.

A. $V = e^{2} - 1$

B. $V = π (e^{2} - 1)$

C. $V = \frac{1}{4} π e^{2} - 1$

D. $V = \frac{1}{4} π (e^{2} - 1)$

Câu 14:

Tìm môđun của số phức $z = (- 4 + i \sqrt{48}) (2 + i)$

A. $8 \sqrt{5}$

B. $5 \sqrt{5}$

C. $6 \sqrt{5}$

D. $9 \sqrt{5}$

Câu 15:

Dạng lũy thừa với số mũ hữu tỉ của biểu thức $\frac{1}{8} \sqrt[7]{2^{5} a x^{3}}$ với a > 0, x > 0 là:

A. $2^{\frac{16}{7}} a^{- \frac{1}{7}} x^{\frac{3}{7}}$

B. $2^{\frac{16}{7}} a^{\frac{1}{7}} x^{- \frac{3}{7}}$

C. $2^{- \frac{16}{7}} a^{\frac{1}{7}} x^{\frac{3}{7}}$

D. $2^{\frac{16}{7}} a^{\frac{1}{7}} x^{\frac{3}{7}}$

Câu 16:

Tìm tất cả các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm

A. Trục hoành (trừ gốc tọa độ O).

B. Đường thẳng y = x (trừ gốc tọa độ O).

C. Trục tung (trừ gốc tọa độ O)

D. Đường thẳng y = -x (trừ gốc tọa độ O).

Câu 17:

Một vật chuyển động với vận tốc 10 (m/s) thì tăng tốc với gia tốc $3 t + t^{2}, (m / s^{2})$ . Quảng đường vật di chuyển trong thời gian 10 giây kể từ lúc bắt đầu tăng tốc

A. 3600 m

B. $\frac{4300}{3}$ m

C. $\frac{1750}{3}$ m

D. $\frac{1450}{3}$ m

Câu 18:

Cho tam giác AOB vuông tại O và OAB = 30 $°$ . Đường cao hạ từ O là OH, OH = a. Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA.

A. $\frac{π}{3} a^{3}$

B. $\frac{9}{10} π a^{3}$

C. $\frac{9}{8} π a^{3}$

D. $\frac{8}{9} π a^{3}$

Câu 19:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình $\frac{x - 1}{2} = \frac{y}{- 5} = \frac{z - 3}{4} .$ Viết phương trình mặt phẳng $(α)$ chứa trục Oy và song song với đường thẳng d

A. -2x + y = 0

B. x - 2z = 0

C. 2x - z = 0

D. 2x + z = 0

Câu 20:

Tìm tập xác định D của hàm số $y = \log (\frac{x - 2}{1 - x})$

A. $D = (- \infty; 1) \cup (2; + \infty)$

B. $D = (1; 2)$

C. $D = ℝ \ \{1\}$

D. $D = ℝ \ (1; 2)$

Câu 21:

Tìm công thức tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P): y = $x^{2}$ và đường thẳng d: y = 2x quay xung quanh trục Ox

A. $π \int_{0}^{2} {(x^{2} - 2 x)}^{2} d x$

B. $π \int_{0}^{2} 4 x^{2} d x - π \int_{0}^{2} x^{4} d x$

C. $π \int_{0}^{2} 4 x^{2} d x + π \int_{0}^{2} x^{4} d x$

D. $π \int_{0}^{2} {(2 x - x^{2})}^{2} d x$

Câu 22:

Đồ thị các hàm số $y = \frac{4 x + 4}{x - 1}$ và $y = x^{2} - 1$ cắt nhau tại bao nhiêu điểm?

A. 0

B. 1

C. 2

D. 3

Câu 23:

Tính môđun số phức nghịch đảo của số phức $z = {(1 - 2 i)}^{2}$

A. $\frac{1}{\sqrt{5}}$

B. $\sqrt{5}$

C. $\frac{1}{25}$

D. $\frac{1}{5}$

Câu 24:

Trong không gian với hệ trục tọa độ Oxyz, tính khoảng cách từ điểm M(1;3;2) đến đường thẳng có phương trình $(d) : \{\begin{cases} x = 1 + t \\ y = 1 + t \\ z = - t \end{cases}$

A. $\sqrt{2}$

B. 2

C. $2 \sqrt{2}$

D. 3

Câu 25:

Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình $\{\begin{cases} x = 6 + t \\ y = - 2 - 5 t \\ z = - 1 + t \end{cases}$ . Xét đường thẳng $∆ : \frac{x - a}{5} = \frac{y - 1}{- 12} = \frac{z + 5}{- 1}$ , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và $∆$ cắt nhau.

A. a = 0

B. a = 4

C. a = 8

D. $a = \frac{1}{2}$

Câu 26:

Xét hàm số $y = f (x) = 2 x^{4} - 3 x^{2} + m$ liên tục trên $[- \frac{1}{2}; 2] .$ Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số trên đoạn đã cho bằng $\frac{31}{8}$

A. m = -4

B. m = $\pm 3$

C. m = 2

D. m = 5

Câu 27:

Có bao nhiêu giá trị m để đồ thị hàm số $y = \frac{m x^{2} - 1}{x^{2} - 3 x + 2}$ có đúng 2 đường tiệm cận?

A. 2

B. $\forall m$

C. 3

D. 1

Câu 28:

Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3;5} có cạnh bằng 1

A. $\frac{5 \sqrt{3}}{2}$

B. $5 \sqrt{3}$

C. $3 \sqrt{3}$

D. $\frac{3 \sqrt{3}}{2}$

Câu 29:

Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2}$ . Hãy tính giá trị của tổng sau:

$P = f (\sin^{2} \frac{π}{2016}) + f (\sin^{2} \frac{2 π}{2016}) + f (\sin^{2} \frac{3 π}{2016}) + . . . + f (\sin^{2} \frac{1008 π}{2016})$

A. $\frac{1007}{2}$

B. $\frac{3025}{6}$

C. $\frac{1511}{3}$

D. $504$

Câu 30:

Biết rằng chỉ có hai giá trị thực khác nhau của tham số m thì đồ thị hàm số $y = \frac{m + 1}{x^{2} - 2 x + m}$ có đúng hai đường tiệm cận; kí hiệu m = a là giá trị thứ nhất, m = a là giá trị thứ hai. Tính ab

A. ab = -1

B. ab = -2

C. ab = -3

D. ab = -4

Câu 31:

Gọi $T = [a; b]$ là tập các giá trị của hàm số $y = \frac{x + 1}{\sqrt{x^{2} + 1}}$ trên [-1;2]. Khẳng định nào sau đây là đúng?

A. $a^{2} + b^{2} = \sqrt{2}$

B. $a^{2} + b^{2} = \frac{9}{5}$

C. $a^{2} + b^{2} = \frac{19}{5}$

D. $a^{2} + b^{2} = 2$

Câu 32:

Biết rằng T=[a;b] là tập tất cả các giá trị thực của tham số m để phương trình $\log_{\frac{1}{3}}^{2} x + \sqrt{\log_{3}^{2} + 1} - 1 - 5 m = 0$ có ít nhất một nghiệm thuộc khoảng $[1; 3^{2 \sqrt{2}}]$ . Tính $a^{2} + b^{2}$

A. $a^{2} + b^{2} = 4$

B. $a^{2} + b^{2} = 6$

C. $a^{2} + b^{2} = 8$

D. $a^{2} + b^{2} = 10$

Câu 33:

Tính tích phân $\int_{1}^{e} \frac{x^{2} + \ln x}{x^{3}} d x = \frac{a}{b} - \frac{3}{4 e^{2}}$ , trong đó a, b dương và $\frac{a}{b}$ là phân số tối giản. Tính ab

A. ab = 10

B. ab = 20

C. ab = 40

D. ab = 30

Câu 34:

Cho số phức z thỏa mãn điều kiện $|z| = 1$ . Tìm giá trị lớn nhất của $A = |1 + z| + 3 |1 - z|$

A. $4 \sqrt{8}$

B. $2 \sqrt{15}$

C. $\sqrt{10}$

D. $2 \sqrt{10}$

Câu 35:

Cho khối tứ diện ABCD có thể tích V. Gọi $G_{1}, G_{2}, G_{3}, G_{4}$ là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện $G_{1} G_{2} G_{3} G_{4}$ là

A. $\frac{V}{27}$

B. $\frac{V}{18}$

C. $\frac{V}{4}$

D. $\frac{V}{12}$

Câu 36:

Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.

A. $V = \frac{4}{3} {πa}^{3}$

B. $V = \frac{4 + 10 \sqrt{2}}{3} {πa}^{3}$

C. $V = \frac{10 \sqrt{2}}{3} {πa}^{3}$

D. $V = \frac{14 \sqrt{2}}{3} {πa}^{3}$

Câu 37:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số $y = x^{3} + x^{2} + m x - 1$ nằm bên phải trục tung. Tìm số phần tử của tập hợp $(- 5; 6) \cap S$

A. 2

B. 5

C. 3

D. 4

Câu 38:

Một chậu nước hình trụ cao 12 cm, rộng 10 cm. Người ta đổ nước vào trong chậu sao cho nước trong chậu cao 10 cm. Sau đó người ta thả các viên bi vào chậu, biết bán kính mỗi viên bi là 2 cm và sau mỗi lần thả viên bi vào thì nước bắn ra ngoài bằng 15% thể tích viên bi. Hỏi cần thả ít nhất bao nhiêu viên bi vào chậu nước thì nước vừa bắn vừa đầy miệng chậu tràn ra ngoài

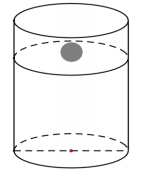
A. 4

B. 5

C. 6

D. 7

Câu 39:

Bạn Linh cần mua một chiếc gương hình dạng đường Parabol bậc 2 (xem hình vẽ).

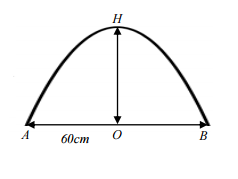
Biết rằng khoảng cách đoạn AB = 60 cm, OH = 30 cm. Diện tích của chiếc gương bạn Linh mua là

A. $1000 (c m^{2})$

B. $1200 (c m^{2})$

C. $1400 (c m^{2})$

D. $900 (c m^{2})$

Câu 40:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I(1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Chọn đẳng thức không đúng khi nói về a, b, c?

A. a + b + c = 12

B. $a^{2} + b = c + 6$

C. a + b + c = 18

D. a + b - c = 0

Câu 41:

Cho $z_{1}, z_{2}$ là hai nghiệm của phương trình $2017 z^{2} - 2016 z + 2017 = 0$ . Tính giá trị của biểu thức $P = {|1 - \vec{z_{1}} . z_{2}|}^{2} - {|z_{1} - z_{2}|}^{2}$

A. 3

B. $\frac{1}{3}$

C. 1

D. 6

Câu 42:

Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là $R \sqrt{17}$ và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón

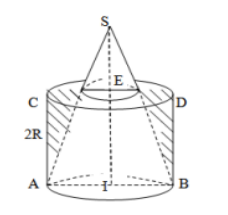
A. $\frac{5}{12} {πR}^{3}$

B. $\frac{1}{3} {πR}^{3}$

C. $\frac{4}{3} {πR}^{3}$

D. $\frac{5}{6} {πR}^{3}$

Câu 43:

Gọi (H) là hình phẳng giới hạn bởi đồ thị (P) của hàm số $y = 6 x - x^{2}$ và trục hoành. Hai đường thẳng $y = m, y = n$ chia hình (H) thành ba phần có diện tích bằng nhau. Tính $P = {(9 - m)}^{3} + {(9 - n)}^{3}$

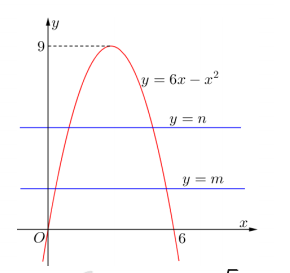
A. P = 405

B. P = 409

C. P = 407

D. P = 403

Câu 44:

Cho x, y là các số thực dương thỏa mãn $\log_{25} \frac{x}{2} = \log_{15} y = \log_{9} \frac{x + y}{4}$ và $\frac{x}{y} = \frac{- a + \sqrt{b}}{2}$ với a, b là các số nguyên dương. Tính a + b

A. 14

B. 3

C. 21

D. 32

Câu 45:

Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân

A. $\frac{2}{35}$

B. $\frac{17}{114}$

C. $\frac{8}{57}$

D. $\frac{3}{19}$

Câu 46:

Tính tổng tất cả các nghiệm của phương trình $e^{\sin (x - \frac{π}{4})} = \tan x$ thuộc đoạn $(0; 50 π)$ ?

A. $\frac{1853 π}{2}$

B. $\frac{2475 π}{2}$

C. $\frac{2671 π}{2}$

D. $\frac{2105 π}{2}$

Câu 47:

Cho phương trình $2 \log_{4} (2 x^{2} - x + 2 m - 4 m^{2}) + \log_{\frac{1}{2}} (x^{2} + m x - 2 m^{2}) = 0$ . Biết rằng $S = (a; b) \cup (c; d), a < b < c < d$ là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa ${x_{1}}^{2} + {x_{2}}^{2} > 1$ . Tính giá trị biểu thức A = a + b + 5c + 2d

A. A = 1

B. A = 2

C. A = 0

D. A = 3

Câu 48:

Gia đình Thầy Hùng ĐZ xây một bể nước dạng hình hộp chữ nhật có nắp dung tích 2018 lít, đáy bể là một hình chữ nhật có chiều dài gấp ba lần chiều rộng được làm bằng bê tông có giá 250.000 đồng/m², thân bể được xây bằng gạch có giá 200.000 đồng/m²và nắp bể làm bằng tôn có giá 100.000 đồng/m². Hỏi chi phí thấp nhất gia đình Thầy cần bỏ ra để xây dựng bể nước là bao nhiêu? (làm tròn đến hàng đơn vị)

A. 2.017.332 đồng

B. 2.017.331 đồng

C. 2.017.333 đồng

D. 2.017.334 đồng

Câu 49:

Một bạn đã cắt tấm bìa carton phẳng và cứng có kích thước như hình vẽ. Sau đó bạn ấy gấp theo đường nét đứt thành một hình hộp chữ nhật. Hình hộp có đáy là hình vuông cạnh a (cm), chiều cao là h (cm) và diện tích tấm bìa là $3 m^{2}$ . Tổng a + h bằng bao nhiêu để thể tích hộp là lớn nhất

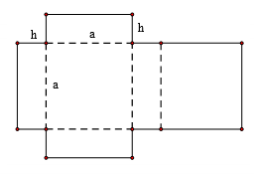
A. $2 \sqrt{2}$

B. $\frac{\sqrt{2}}{2}$

C. 46,3

D. $\sqrt{2}$

Câu 50:

Cho hàm số $y = x^{3} - \frac{3}{4} x^{2} - \frac{3}{2} x$ có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m sao cho phương trình $4 |x^{3}| - 3 x^{2} - 6 |x| = m^{2} - 6 m$ có đúng ba nghiệm phân biệt

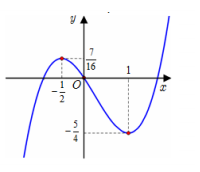
A. m = 0 hoặc m = 6

B. m < 0 hoặc m > 6

C. 0 < m < 3

D. 1 < m < 6

Đề số 6

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề số 6

CHỌN BỘ SÁCH BẠN MUỐN XEM