Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 30)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
Với a là số thực dương tùy ý, bằng:
A.
B.
C.
D.
Tập nghiệm của phương trình là:
A.
B.
C.
D. S = {4}.
Cho cấp số nhân có và Giá trị của là:
A.
B.
C.
D.
A. x = 1
B. y = 1
C. y = -1
D. x = -1
A.
B.
C.
D.
Môđun của số phức bằng:
A.
B.
C.
D.
Đạo hàm của hàm số là:
A.
B.
C.
D.
Cho hàm số f(x) có bảng biến thiên như sau:
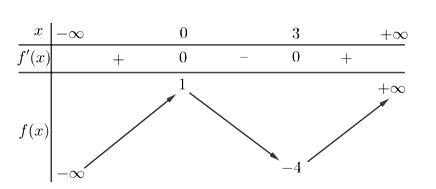
Điểm cực tiểu của hàm số đã cho là:
A. x = -4
B. x = 0
C. x = 3
D. x = 1
Nghiệm của phương trình là
A. x = -3
B. x = 3
C. x = 1
D. x = -1
A. (-2; 1)
B. (-2; -1)
C. (2; 1)
D. (2; -1)
Cho hàm số f(x) = sin3x. Khẳng định nào sau đây đúng:
A.
B.
C.
D.
Cho hai số phức Số phức bằng:
A. w = -8 - i
B. w = 8 - i
C. w = -8 + i
D. w = 8 + i
Cho Khi đặt t = 2x thì ta được:
A.
B.
C.
D.
Cho hai hàm số f(x), g(x) thỏa mãn Giá trị là:
A. I = 7
B. I = -3
C. I = 3
D. I = -7
Cho hàm số f(x) có bảng xét dấu của đạo hàm f'(x) như sau:
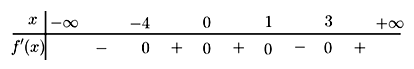
Số điểm cực trị của hàm số f(x) đã cho là:
Có bao nhiêu cách chọn ra 2 học sinh trong 8 học sinh:
A.
B. 6!
C.
D.
Cho hàm số f(x) có bảng biến thiên như sau:
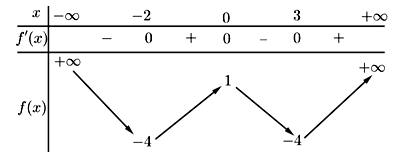
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
B.
C. (-2; 3)
D. (0; 3)
Cho F(x) là một nguyên hàm của hàm số f(x) = 2 và F(0) = 2. Tìm F(x)?
A. F(x) = 2
B. F(x) = 2x + 1
C.
D.
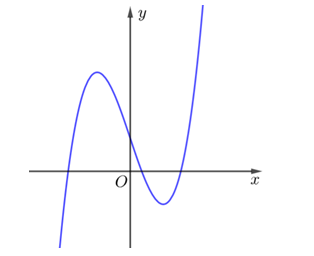
A.
B.
C.
D.
Tổng hai nghiệm của phương trình bằng:
Cho hàm số f(x) liên tục trên và Tính
A. I = 1
B. I = 4
C. I = 2
D. I = 3
Trong không gian tọa độ Oxyz, cho ba điểm và C(0; 2; 3). Trọng tâm G của tam giác ABC có tọa độ là:
A. (1; 2; 1)
B. (2; 0; -1)
C. (1; 1; 1)
D. (1; 1; -2)
Một lớp có 38 học sinh, trong đó có 20 học sinh nam. Chọn ngẫu nhiên một học sinh. Tính xác suất để chọn được một học sinh nữ.
A.
B.
C.
D.
Trong không gian tọa độ Oxyz, cho mặt phẳng và điểm A(1; 1; 4). Tìm giá trị của tham số m để điểm A thuộc (P)?
A. m = 5
B. m = 4
C. m = 9
D. m = 3
Cho số phức z = a + bi thỏa mãn Tính a - b?
A.
B.
C.
D.
Biết giá trị lớn nhất của hàm số trên đoạn [0; 2] bằng 5, tìm giá trị của tham số m
Cho hình lăng trụ đứng có diện tích đáy là độ dài cạnh bên bằng 2a. Thể tích khối lăng trụ này bằng:
A.
B.
C.
D.
Hàm số nghịch biến trên khoảng nào sau đây?
A. (0; 2)
B. (-2; -1)
C. (-1; 0)
D. (-2; 0)
Trong không gian tọa độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(1; 1; 1) và có vectơ pháp tuyến là:
A.
B.
C.
D.
Cho khối hộp ABCD.A'B'C'D' có thể tích V = 2021. Tính thể tích của khối lăng trụ ABC.A'B'C'.
A.
B.
C.
D.
Cho hình nón có đường sinh l =6, bán kính đáy r = 2. Diện tích toàn phần của hình nón bằng:
A.
B.
C.
D.
Trong không gian tọa độ Oxyz, mặt cầu (S) tâm I(-1; 0; 2) và bán kính R = 4 có phương trình là:
A.
B.
C.
D.
A.
B.
C.
D.
Cho số phức thỏa mãn Tính S = 2a + 3b
A. S = 5
B. S = 6
C. S = -5
D. S = -6
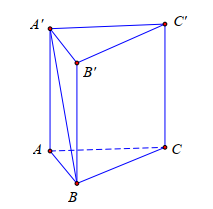
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B với (tham khảo hình vẽ). Tính góc giữa đường thẳng A'B và mặt phẳng (ABC)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng Phương trình mặt cầu (S) có tâm O và tiếp xúc với mặt phẳng (P) là:
A.
B.
C.
D.
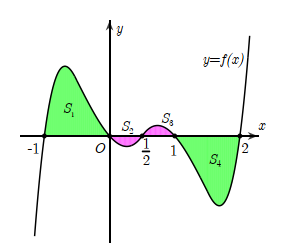
Cho hàm số y = f(x) liên tục trên có đồ thị tạo với trục hoành các miền có diện tích (như hình vẽ) và Biết tích phân với là phân số tối giản. Tính tích ab?
Trong không gian Oxyz, cho hai điểm Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
A.
B.
C.
D.
Trong không gian Oxyz, cho ba đường thẳng và Gọi (P) là mặt phẳng chứa đường thẳng cắt các đường thẳng lần lượt tại A và sao cho đường thẳng AB vuông góc với Phương trình của mặt phẳng (P) là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và điểm M là trung điểm của SA. Biết thể tích khối chóp A.SBC bằng và tính khoảng cách từ M đến mặt phẳng (ABCD).
A.
B.
C.
D.
Cho hai số phức thỏa mãn và Gọi số phức z = a + bi thỏa mãn 3a - 2b = 12. Giá trị nhỏ nhất của bằng
A.
B.
C.
C.
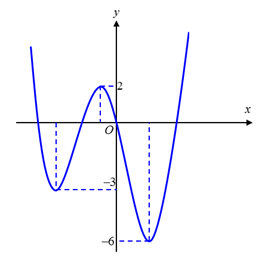
Cho hàm số f(x) liên tục trên và đồ thị hàm số y = f(x) cắt trục hoành tại các điểm có hoành độ lần lượt là (như hình bên dưới). Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên [a; c] bằng 2021. Tổng tất cả các phần tử của S bằng:
A. -36
B. -2022
C. -2021
D. 24
Gọi A, B, C là 3 điểm có hoành độ thỏa mãn và tung độ bằng nhau, lần lượt thuộc đồ thị hàm số Tính độ dài đoạn thẳng AB?
Trong hệ tọa độ Oxyz, cho tam giác ABC với Gọi M là một điểm di động trên mặt cầu sao cho hình chiếu vuông góc của M lên các cạnh lần lượt là H, K, E. Hỏi có bao nhiêu điểm M thuộc mặt cầu (S) sao cho đạt giá trị nhỏ nhất.
Có bao nhiêu giá trị nguyên để phương trình sau: có nghiệm thực?
A.
B.
C.
D.
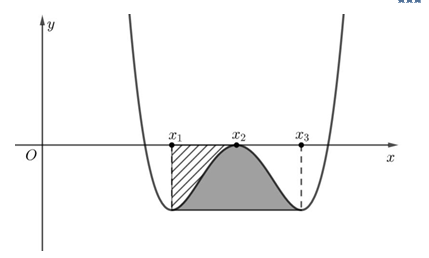
Cho hàm số bậc bốn f(x) thỏa mãn và đồ thị y = f'(x) (như hình vẽ bên dưới).
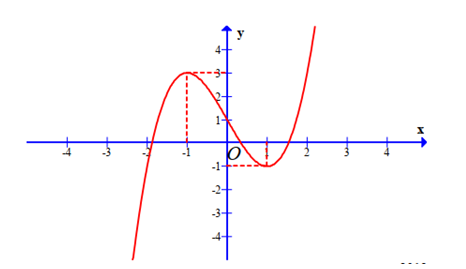
Xét hàm số f(x) thỏa mãn và Tìm số nghiệm của phương trình g'(x) = 0.
Một xí nghiệp chế biến sữa bò muốn sản xuất lon đựng sữa có dạng hình trụ bằng thiếc có thể tích không đổi. Để giảm giá một lon sữa khi bán ra thị trường người ta cần chế tạo lon sữa có kích thước sao cho ít tốn kém vật liệu. Để thỏa mãn yêu cầu đặt ra (diện tích toàn phần bé nhất), người ta phải thiết kế lon sữa thỏa mãn điều kiện nào trong các điều kiện sau:
A. Chiều cao bằng 3 lần bán kính của đáy
B. Chiều cao bằng bình phương bán kính của đáy.
C. Chiều cao bằng đường kính của đáy.