Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 4)

Câu 1:

Có bao nhiêu cách sắp xếp 5 học sinh vào một ghế dài từ một nhóm gồm 10 học sinh?

A. $10^{5} .$

B. $5^{10} .$

C. $C_{10}^{5} .$

D. $A_{10}^{5} .$

Câu 2:

Cho cấp số cộng $(u_{n})$ với $u_{1} = 5$ và $u_{2} = 15.$ Công sai của cấp số cộng đã cho bằng

A. 20.

B. 75.

C. 3.

D. 10.

Câu 3:

Nghiệm của phương trình

5^{x + 1} = 125

là

A. x = 2

B. x = 3

C. x = 0

D. x = 1

Câu 4:

Thể tích của khối lập phương cạnh $2 \sqrt{3}$ bằng

A. $24 \sqrt{3} .$

B. $54 \sqrt{2} .$

C. 8

D. $18 \sqrt{2}$

Câu 5:

Tập xác định của hàm số

y = \log_{2} (3 x - 6)

là

A. $(- \infty; 2) .$

B. $(2; + \infty)$

C. $(- \infty; + \infty)$

D. $(0; + \infty)$

Câu 6:

Tìm nguyên hàm của hàm số $f (x) = x^{2021}$ trên $ℝ .$

A. $\int f (x) d x = \frac{x^{2022}}{2022} .$

B. $\int f (x) d x = 2021 x^{2020} + C .$

C. $\int f (x) d x = \frac{x^{2022}}{2022} + C .$

D. $\int f (x) d x = \frac{x^{2021}}{2021} + C .$

Câu 7:

Cho khối lăng trụ có diện tích đáy B = 5 và chiều cao h = 6. Thể tích của khối lăng trụ đã cho bằng

A. 15.

B. 30.

C. 150.

D. 10.

Câu 8:

Cho khối lăng trụ có chiều cao h = 3 và bán kính đáy r = 2. Thể tích của khối trụ đã cho bằng

A. $V = 18 π .$

B. $V = 6 π .$

C. $V = 4 π .$

D. $V = 12 π .$

Câu 9:

Cho mặt cầu có bán kính R = 6. Diện tích S của mặt cầu đã cho bằng

A. $S = 144 π .$

B. $S = 38 π .$

C. $S = 36 π .$

D. $S = 288 π .$

Câu 10:

Cho hàm số y = f(x) có bảng biến thiên như sau

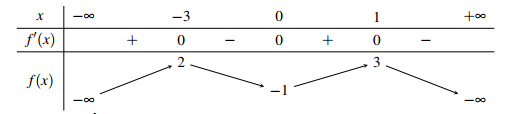
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (-3; 1)

B. $(1; + \infty) .$

C. $(- \infty; 0) .$

D. (0; 1)

Câu 11:

Với a là số thực dương tùy ý, $\log_{3} (a^{5})$ bằng

A. $\frac{1}{5} \log_{3} a .$

B. $5 \log_{3} a .$

C. $5 + \log_{3} a .$

D. $\frac{3}{5} \log_{3} a .$

Câu 12:

Cho hình nón có bán kính đáy là r đường cao h và đường sinh l. Diện tích xung quanh $S_{x q}$ hình nón đó là

A. $S_{x q} = \frac{1}{3} π r^{2} h .$

B. $S_{x q} = π r l .$

C. $S_{x q} = 2 π r l .$

D. $S_{x q} = π r h .$

Câu 13:

Cho hàm số có bảng biến thiên như sau:

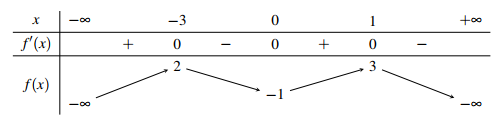
Hàm số đã cho đạt cực đại tại

A. x = 2

B. x = -3

C. x = -1

D. x = 0

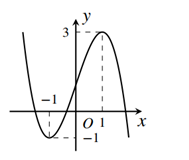
Câu 14:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. $y = x^{3} - 3 x + 1.$

B. $y = - x^{3} + 3 x + 1.$

C. $y = - x^{4} + 2 x^{2} + 1.$

D. $y = x^{4} - 2 x^{2} + 1.$

Câu 15:

Đồ thị hàm số $y = \frac{3 x - 2}{2 x - 4}$ có tiệm cận đứng và tiệm cận ngang tương ứng là x = a, y = b. Khi đó a.b bằng

A. 3

B. -3

C. $\frac{1}{2} .$

D. $- \frac{1}{2}$

Câu 16:

Tập nghiệm của bất phương trình $\log_{\frac{1}{3}} x \geq - 2$ là

A. $[0; + \infty)$

B. $(- \infty; 9)$

C. $(0; 9]$

D. $(9; + \infty)$

Câu 17:

Cho hàm số trùng phương y = f(x) có đồ thị hình bên. Số nghiệm của phương trình f(x) = 0,5 là

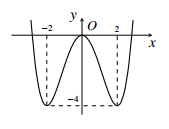
Cho hàm số trùng phương y = f(x) có đồ thị hình bên. Số nghiệm của phương trình (ảnh 1)

A. 2

B. 1

C. 3

D. 4

Câu 18:

Nếu

\int_{0}^{1} f (x) d x = 4

và

\int_{0}^{1} g (x) d x = 3

thì

\int_{0}^{1} [2 f (x) + 3 g (x)] d x

bằng

A. 7

B. 13

C. 17

D. 11

Câu 19:

Số phức liên hợp của số phức

z = (2 - 3 i) (4 + i)

là

\bar{z} = a + b i .

Khi đó a + b bằng

A. -21

B. 1

C. 21

D. -1

Câu 20:

Cho số phức z thỏa mãn phương trình

(2 - i) z + 1 = 3 i .

Phần thực của số phức z bằng

A. -2

B. -1

C. 2

D. 1

Câu 21:

Trên mặt phẳng tọa độ Oxy điểm biểu diễn số phức

z = z_{1} + z_{2}

(với

z_{1} = 5 + 3 i

và

z_{2} = 6 + 4 i

) là điểm nào dưới đây?

A. M(1; -1)

B. Q(11; 7)

C. P(-1; -1)

D. N(-11; -7)

Câu 22:

Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2; 3; -4) trên mặt phẳng (Oyz) có tọa độ là

A. (2; 3; 0)

B. (0; 3; 0)

C. (0; 3; -4)

D. (2; 0; -4)

Câu 23:

Trong không gian Oxyz, mặt cầu (S) có tâm I(-2; 3; 4) và đi qua M(0; 2; 2) có phương trình là

A. $(S) : {(x + 2)}^{2} + {(y - 4)}^{2} + {(z - 3)}^{2} = 3.$

B. $(S) : {(x - 2)}^{2} + {(y + 4)}^{2} + {(z + 3)}^{2} = 9.$

C. $(S) : {(x - 2)}^{2} + {(y + 4)}^{2} + {(z + 3)}^{2} = 3.$

D. $(S) : {(x + 2)}^{2} + {(y - 4)}^{2} + {(z - 3)}^{2} = 9.$

Câu 24:

Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x + 3 y + 2 = 0.$ Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?

A. $\vec{n} = (- 2; - 3; 1) .$

B. $\vec{n} = (- 2; - 3; 0)$

C. $\vec{n} = (2; 3; 1)$

D. $\vec{n} = (2; 3; 2)$

Câu 25:

Trong không gian Oxyz, cho mặt phẳng $(α) : 2 x + 2 y - z + m = 0$ (m là tham số). Tìm giá trị m dương để khoảng cách từ gốc tọa độ đến $(α)$ bằng 1.

A. m = -3

B. m = 3

C. m = -6

D. m = 6

Câu 26:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), $S A = \sqrt{2} a,$ tam giác ABC vuông tại A và $A C = a, \sin B = \frac{1}{\sqrt{3}}$ (minh họa như hình bên). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng

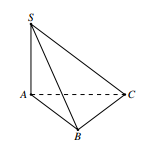
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = căn bậc hai của 2.a (ảnh 1)

A. $90^{0}$

B. $30^{0}$

C. $45^{0}$

D. $60^{0}$

Câu 27:

Cho hàm số f(x) xác định trên $ℝ$ và có bảng xét dấu của f'(x) như sau

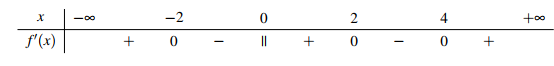
Cho hàm số f(x) xác định trên R và có bảng xét dấu của f'(x) như sau (ảnh 1)

Số điểm cực tiểu của hàm số đã cho là

A. 2

B. 4

C. 3

D. 1

Câu 28:

Biết rằng giá trị lớn nhất của hàm số

y = x + \sqrt{4 - x^{2}} + m

là

3 \sqrt{2} .

Giá trị của m là

A. $m = 2 \sqrt{2}$

B. $m = - \sqrt{2}$

C. $m = \frac{\sqrt{2}}{2}$

D. $m = \sqrt{2}$

Câu 29:

Cho $a > 0, b > 0$ và a khác 1 thỏa mãn $\log_{a} b = \frac{b}{4}; \log_{2} a = \frac{16}{b} .$ Tính tổng a + b.

A. 32

B. 16

C. 18

D. 10

Câu 30:

Số giao điểm của đồ thị hàm số $y = x^{4} - 2 x^{2} + 1$ và đường thẳng y = 4 là

A. 4

B. 2

C. 3

D. 1

Câu 31:

Tập nghiệm của bất phương trình $\log_{\frac{1}{2}} (\log_{2} \frac{3 x - 1}{x + 1}) \leq 0$ là

A. $(- \infty; - 1)$

B. $[3; + \infty)$

C. $(- \infty; - 1) \cup [3; + \infty)$

D. $(- 1; 3]$

Câu 32:

Cho hình nón có chiều cao h = 20cm, bán kính đáy r = 25cm. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích S của thiết diện đó.

A. $S = 500 c m^{2} .$

B. $S = 300 c m^{2}$

C. $S = 406 c m^{2}$

D. $S = 400 c m^{2}$

Câu 33:

Khi đổi biến

x = \sqrt{3} \tan t,

tích phân

I = \int_{0}^{1} \frac{d x}{x^{2} + 3}

trở thành tích phân nào?

A. $I = \int_{0}^{\frac{π}{3}} \frac{\sqrt{3}}{3} d t$

B. $I = \int_{0}^{\frac{π}{6}} \frac{1}{t} d t$

C. $I = \int_{0}^{\frac{π}{6}} \frac{\sqrt{3}}{3} d t$

D. $I = \int_{0}^{\frac{π}{6}} \sqrt{3} t d t$

Câu 34:

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số $(H) : y = \frac{x - 1}{x + 1}$ và các trục tọa độ. Khi đó giá trị của S bằng

A. S = ln2 + 1

B. S = 2ln2 +1

C. S = ln2 - 1

D. S = 2ln2 - 1

Câu 35:

Điểm biểu diễn của các số phức z = 7 + bi với $b \in ℝ$ nằm trên đường thẳng có phương trình là

A. x = 7

B. y = 7

C. x = -7

D. y = -7

Câu 36:

Cho số phức z thỏa mãn |z| = 2. Biết rằng tập hợp các điểm biểu diễn số phức

w = 3 - 2 i + (2 - i) z

là một đường tròn. Bán kính R của đường tròn đó bằng

A. 2

B. 5

C. $2 \sqrt{5}$

D. $\sqrt{5}$

Câu 37:

Trong không gian Oxyz, mặt phẳng (P) đi qua điểm A(0; -2; 3) và song song với mặt phẳng $(α) : - 2 x + y - 3 z + 2 = 0$ có phương trình là

A. $(P) : 2 x - y + 3 z - 9 = 0$

B. $(P) : x - y - 3 z + 11 = 0$

C. $(P) : 2 x - y + 3 z - 11 = 0$

D. $(P) : 2 x - y + 3 z + 11 = 0$

Câu 38:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(-3; 1; 4) và gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Phương trình nào dưới đây là phương trình cuả mặt phẳng song song với mặt phẳng (ABC)?

A. $4 x - 12 y + 3 z - 12 = 0$

B. $4 x + 12 y - 3 z - 12 = 0$

C. $4 x - 12 y - 3 z + 12 = 0$

D. $4 x - 12 y - 3 z - 12 = 0$

Câu 39:

Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1; 17]. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng

A. $\frac{3276}{4913}$

B. $\frac{1728}{4913}$

C. $\frac{23}{68}$

D. $\frac{1637}{4913}$

Câu 40:

Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = a và OB = OC = 2a. Gọi P là trung điểm của BC (minh họa như hình bên). Khoảng cách giữa hai đường thẳng OP và AB bằng

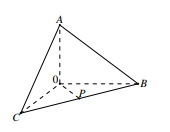
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = a (ảnh 1)

A. $\frac{\sqrt{2} a}{2} .$

B. $\frac{\sqrt{6} a}{3} .$

C. a.

D. $\frac{2 \sqrt{5} a}{5} .$

Câu 41:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{1}{3} x^{3} - (m - 1) x^{2} - 4 m x$ đồng biến trên đoạn [1; 4].

A. $\frac{1}{2} < m < 2$

B. $m \in ℝ$

C. $m \leq 2$

D. $m \leq \frac{1}{2} .$

Câu 42:

Ông An muốn xây một bể nước dạng hình hộp chữ nhật có nắp với dung tích 3 mét khối. Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500000 đồng cho mỗi mét vuông. Hỏi chi phí thấp nhất ông An cần bỏ ra để xây bể nước là bao nhiêu?

A. 6490123 đồng

B. 7500000 đồng

C. 6500000 đồng

D. 5151214 đồng.

Câu 43:

Cho hàm số $f (x) = \frac{a x - 4}{b x + c} (a, b, c \in ℝ)$ có bảng biến thiên như sau

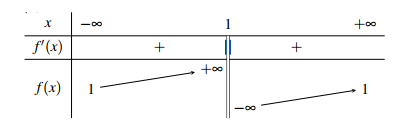
Cho hàm số f(x) = ax - 4/bx + c (a, b, c thuộc R) có bảng biến thiên như sau (ảnh 1)

Trong các số a, b, c có bao nhiêu số dương?

A. 3

B. 4

C. 2

D. 1

Câu 44:

Một nhà máy cần sản xuất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là

A. h = R

B. h = 3R

C. h = 2R

D. R = 2h

Câu 45:

Cho hàm số y = f(x) có đạo hàm liên tục trên

ℝ

thỏa mãn

f (x) + f (\frac{π}{2} - x) = \sin x . \cos x,

với mọi

x \in ℝ

và f(0) = 0. Giá trị của tích phân

\int_{0}^{\frac{π}{2}} x . f' (x) d x

bằng

A. $\frac{1}{4} .$

B. $\frac{π}{4} .$

C. $- \frac{1}{4} .$

D. $- \frac{π}{4} .$

Câu 46:

Có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số $y = \frac{\tan x - 2}{\tan x - m}$ đồng biến trên khoảng $(- \frac{π}{4}; 0) ?$

A. Có vô số

B. 0

C. 2

D. 1

Câu 47:

Cho 2 số thực dương x, y thỏa mãn

\log_{3} {[(x + 1) (y + 1)]}^{y + 1} = 9 - (x - 1) (y + 1) .

Giá trị nhỏ nhất của biểu thức P = x + 2y là

A. $P_{\min} = \frac{11}{2} .$

B. $P_{\min} = \frac{27}{5} .$

C. $P_{\min} = - 5 + 6 \sqrt{3} .$

D. $P_{\min} = - 3 + 6 \sqrt{2} .$

Câu 48:

Xét hàm số

f (x) = |x^{2} + a x + b|,

với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên [-1; 3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.

A. 5

B. -5

C. -4

D. 4

Câu 49:

Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh DD' sao cho

D P = \frac{1}{4} D D' .

Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng

A. $V = 3 a^{3} .$

B. $V = \frac{a^{3} \sqrt{11}}{3}$

C. $V = 2 a^{3} .$

D. $V = \frac{a^{3} \sqrt{9}}{4}$

Câu 50:

Cho a là số thực dương sao cho $3^{x} + a^{x} \geq 6^{x} + 9^{x}$ với mọi $x \in ℝ .$ Mệnh đề nào sau đây đúng?

A. $a \in (14; 16] .$

B. $a \in (16; 18] .$

C. $a \in (12; 14] .$

D. $a \in (10; 12] .$

Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 4)

Giới thiệu

Liên kết

Chính sách

Kết nối

Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 4)

CHỌN BỘ SÁCH BẠN MUỐN XEM