Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 3)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
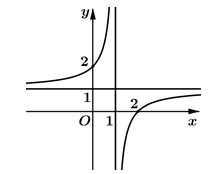
A.
B.
C.
D.
Cho hàm số . Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên
B. Hàm số đã cho đồng biến trên
C. Hàm số đã cho đồng biến trên
D. Hàm số đã cho đồng biến trên
Tìm điểm cực đại của hàm số
A. = -1
B. = 0
C. = 1
D. = 2
Cho hàm số y = f(x) có bảng biến thiên như sau
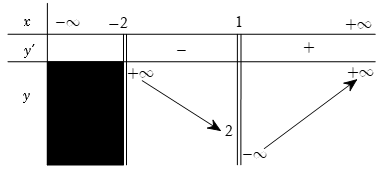
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Với a, b, x là các số thực dương thỏa mãn . Mệnh đề nào sau đây đúng?
A. x = 3a + 4b
B. x = 4a + 3b
C.
D.
Tìm đạo hàm của hàm số
A.
B.
C.
D.
Tìm số nghiệm nguyên dương của phương trình
A. 0
B. 1
C. 2
D. 4
Tìm tập nghiệm của bất phương trình
A. S = (-1;1)
B. S = (0;1)
C. S = (-1;0)
D. S = (-1;1)\{0}
Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất . Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được một năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?
A. 210 triệu.
B. 212 triệu.
C. 216 triệu.
D. 220 triệu.
Cho hai hàm số và . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1, b = -7
B. a = -1, b = -7
C. a = -1, b = =7
D. a = 1, b = 7
Biết rằng với a và b là các số hữu tỉ. Tính
A.
B.
C.
D.
Hình vẽ bên biểu diễn trục hoành cắt đồ thị y = f(x) tại ba điểm có hoành độ . Gọi S là hình phẳng giới hạn bởi đồ thị y = f(x) và trục hoành, khẳng định nào sau đây sai?
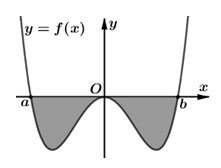
A.
B.
C.
D.
Một ô tô đang chạy với vận tốc 10(m/s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quảng đường ô tô di chuyển được trong 8 giây cuối cùng.
A. 16m
B. 25m
C. 50m
D. 55m
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
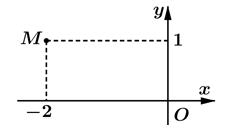
A. = 1 - 2i
B. = 1 + 2i
C. = -2 + i
D. = 2 + i
Cho số phức . Số phức z có phần ảo là
A. -2
B. 2
C. 4
D. 2i
Tìm hai số thực x và y thỏa với i là đơn vị ảo.
A. x = -1, y = -3
B. x = -1, y = -1
C. x = 1, y = -1
D. x = 1, y = -3
Cho số phức z thỏa mãn . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức . Tính
A. P = 5
B. P = 7
C. P = 13
D. P = 25
Trong tam giác Pascal, tính tổng của tất cả các số hạng từ hàng thứ 1 đến hàng thứ 11
A. 1023
B. 2047
C. 8191
D. 4095
Tính tổng S =
A.
B.
C.
D.
An chọn ngẫu nhiên một số thực bất kỳ thuộc đoạn {0;3}. Bình chọn ngẫu nhiên một số thực bất kỳ thuộc đoạn [0;6]. Xác suất để số của Bình lớn hơn số của An bằng
A.
B.
C.
D.
Cho là một cấp số cộng có tổng n số hạng đầu tính được theo công thức với . Số hạng đầu và công sai d của cấp số cộng đó là
A.
B.
C.
D.
Ông Nam đã trồng cây ca cao trên mảnh đất của mình có dạng hình tam giác, ông trồng ở hàng đầu tiên cây ca cao, kể từ hàng thứ hai trở đi số cây ca cao phải trồng ở mỗi hàng nhiều hơn cây so với số cây đã trồng ở hàng trước đó và ở hàng cuối cùng ông đã trồng 2018 cây ca cao. Số cây ca cao mà ông Nam đã trồng trên mảnh đất của mình là
A. 407231 cây
B. 407232 cây
C. 408242 cây
D. 408422 cây
Giá trị bằng
A. 1
B. 2
C. 3
D.
Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến vuông góc với đường thẳng
A. y = 45x - 173; y = 45x + 83
B. y = 45x - 173
C. y = 45x + 173; y = 45x - 83
D. y = 45x - 83
Cho hình chóp S.ABCD có đáy ABCD là hình thang với . Gọi I là giao điểm của AC và BD. Trên cạnh SB lấy điểm M. Giao tuyến của hai mặt phẳng (ADM) và (SAC) là
A. SI
B. AE (E là giao điểm của DM và SI).
C. DM
D. DE (E là giao điểm của DM và SI).
Cho hình lăng trụ đều ABC.A'B'C' có và AA' = 1. Góc tạo bởi giữa đường thẳng AC' và (ABC) bằng
A. 30
B. 45
C. 60
D. 75
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' bằng
A. a
B. a
C.
D.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng AB' và BC' bằng
A. 30
B. 45
C. 60
D. 90
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, . Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng
A.
B. a
C.
D.
Hình đa diện trong hình vẽ bên có bao nhiêu cạnh?
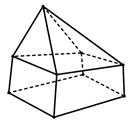
A. 8
B. 9
C. 12
D. 16
Cho hình lăng trụ tam giác đều có cạnh đáy bằng 2a và có các mặt bên đều là hình vuông. Thể tích khối lăng trụ đã cho bằng
A.
B.
C.
D.
Cho hình thang ABCD vuông A và B với . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A.
B.
C.
D.
Một cơ sở sản xuất kem chuẩn bị làm 1000 chiếc kem giống nhau theo đơn đặt hàng. Cốc đựng kem có dạng hình tròn xoay được tạo thành khi quay hình thang ABCD vuông tại A và D xung quanh trục AD(xem hình vẽ). Chiếc cốc có bề dày không đáng kể, chiều cao 7,2 cm đường kính miệng cốc bằng 6,4 cm đường kính đáy cốc bằng 1,6 cm. Kem được đổ đầy cốc và dư ra phía ngoài một lượng có dạng nửa hình cầu, có bán kính bằng bán kính miệng cốc. Cơ sở đó cần dùng lượng kem gần nhất với giá trị nào trong các giá trị sau
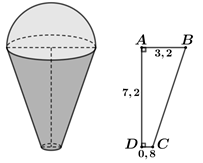
A. 132
B. 170
C. 293
D. 954
Trong không gian với hệ tọa độ Oxyz cho sáu điểm , A', B', C' thỏa mãn . Nếu G' là trọng tâm tam giác A'B'C' thì G' có tọa độ là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho là phương trình mặt cầu, với a, b, c là các số thực và . Khẳng định nào sau đây đúng?
A. luôn đi qua gốc tọa độ
B. (S) tiếp xúc với mặt phẳng O
C. (S) tiếp xúc với trục Oz
D. (S) tiếp xúc với các mặt phẳng (Oyz) và (Ozx)
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng và điểm I(1;-1;2). Phương trình mặt phẳng đối xứng với qua I là
A. : 4x - 3y - 7z - 3 = 0
B. : 4x - 3y - 7z + 11 = 0
C. : 4x - 3y - 7z - 11 = 0
D. : 4x - 3y - 7z + 5 = 0
Trong không gian với hệ tọa độ Oxyz lấy các điểm A(a;0;0), B(0;b;0), C(0;0;c) trong đó và . Khi a, b, c thay đổi, mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ
A. (1;1;1)
B. (2;2;2)
C.
D.
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d: . Đường thẳng d đi qua điểm nào dưới đây?
A. M(1;5;4)
B. M(-1;-2;-5)
C. M(0;3;-1)
D. M(1;2;-5)
Trong không gian với hệ tọa độ Oxyz cho đường thẳng và hai điểm M(-1;3;1), N(0;2;-1). Điểm thuộc d sao cho tam giác MNP cân tại P. Khi đó bằng
A.
B. 1
C. 2
D. 3
Cho đa thức f(x) hệ số thực và thỏa điều kiện . Tìm tất cả các giá trị của tham số thực m để hàm số đồng biến trên
A.
B.
C.
D. m > 1
Cho hàm số y = f(x) có đạo hàm trên và có bảng xét dấu của
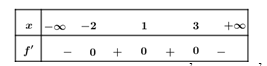
Hỏi hàm số có bao nhiêu điểm cực tiểu?
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình vẽ bên. Xét hàm số . Tìm m để
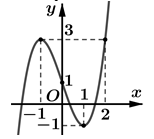
A. m = -13
B. m = -12
C. m = -1
D. m = 3
Cho hàm số y = f(x). Hàm số có đồ thị như hình bên. Biết f(-1) = 1, . Bất phương trình f(x) < ln(-x) + m đúng với mọi khi và chỉ khi
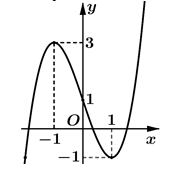
A. m > 2
B.
C. m > 3
D.
Cho a,b là các số thực thỏa mãn và . Giá trị lớn nhất của biểu thức P = 2a + 4b - 3 bằng
A.
B.
C.
D. 2
Cho hàm số f(x) có đạo hàm liên tục trên thỏa mãn và Tích phân bằng
A. I = -13
B. I = -7
C. I = 7
D. I = 13
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình. Tập hợp tất cả các giá trị thực tham số m để phương trình f(cosx) = m có 3 nghiệm phân biệt thuộc khoảng là
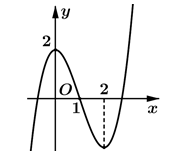
A. [-2;2]
B. (0;2)
C. (-2;2)
D. (0;2]
Hai chuồng nhốt thỏ, mỗi con thỏ có lông chỉ mang màu trắng hoặc màu đen. Bắt ngẫu nhiên mỗi chuồng một con thỏ. Biết tổng số thỏ trong hai chuồng là và xác suất để bắt được hai con thỏ lông màu đen là . Xác suất để bắt được hai con thỏ lông màu trắng bằng
A.
B.
C.
D.
Cho hình chóp S.ABC có , tất cả các cạnh còn lại đều bằng 1. Thể tích lớn nhất của khối chóp đã cho bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho điểm A(0;1;2) mặt phẳng và . Gọi (P) là mặt phẳng đi qua A vuông góc với và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx' là
A.
B.
C.
D.