Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 4)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
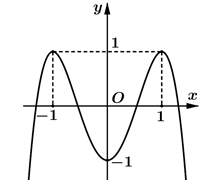
A.
B.
C.
D.
Cho hàm số y = f(x) liên tục trên và có bảng biên thiên như sau
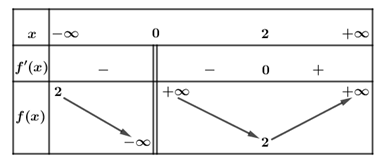
Khẳng định nào sau đây đúng?
A. f(-5) > f(-4)
B. Hàm số đồng biên trên khoảng
C. Hàm số có giá trị nhỏ nhất bằng 2
D. Đường thẳng x = 2 là đường tiệm cận đứng của đồ thị hàm số.
Cho hàm số y = f(x) liên tục trên với bảng xét dấu đạo hàm như sau
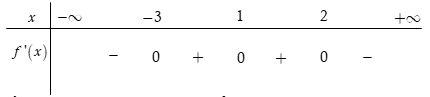
Hỏi hàm số y = f(x) có bao nhiêu điểm cực trị?
A. 0
B. 1
C. 2
D. 3
Gọi là giá trị cực tiểu của hàm số trên . Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Một sợi dây kim loại dài 32 cm được cắt thành hai đoạn bằng nhau. Đoạn thứ nhất uốn thành một hình chữ nhật có chiều dài 6cm, chiều rộng 2 cm. Đoạn thứ hai uốn thành một tam giác có độ dài một cạnh bằng 6cm. Gọi độ dài hai cạnh còn lại của tam giác là x(cm), y(cm) . Hỏi có bao nhiêu cách chọn bộ số (x;y) sao cho diện tích của tam giác không nhỏ hơn diện tích hình chữ nhật?
A. 0 cách
B. 1 cách
C. 2 cách
D. Vô số cách
Cho và với . Chọn khẳng định đúng
A. A = (3 - a).a
B. A = (3 + a).a
C.
D.
Hệ số góc của tiếp tuyến với đồ thị hàm số y = ln(x+1) tại điểm có hoành độ x = 2 là
A.
B. 1
C. ln2
D.
Tổng lập phương các nghiệm của phương trình bằng
A. 6
B. 26
C. 126
D. 216
Cho phương trình . Tập tất cả các giá trị của tham số m để phương trình đã cho có nghiệm phân biệt là
A.
B.
C.
D.
Một người muốn gửi tiền vào ngân hàng để đến ngày rút được khoản tiền là . Lãi suất ngân hàng là . Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi vào ngày người đó phải gửi ngân hàng số tiền là bao nhiêu để đáp ứng nhu cầu trên, nếu lãi suất không thay đổi trong thời gian người đó gửi tiền?
A. 43.593.000 đồng
B. 43.833.000 đồng
C. 44.316.000 đồng
D. 44.074.000 đồng
Trong các khẳng định sau, khẳng định nào sai?
A. (C là hằng số)
B. (C là hằng số)
C. (C là hằng số)
D. (C là hằng số)
Tích phân bằng
A.
B.
C.
D.
Cho hình phẳng H giới hạn bởi đường tròn có bán kính , đường cong và trục hoành (miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình H quay quanh trục Ox
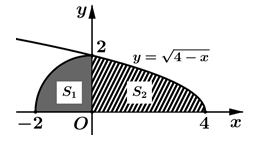
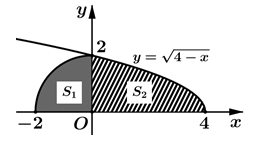
A.
B.
C.
D.
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là và . Biết , tính f(2)

A.
B.
C.
D.
Một vật đang chuyển động với vận tốc 6 m/s thì tăng tốc với gia tốc , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu tăng tốc. Hỏi vận tốc của vật sau giây gần nhất với kết quả nào sau đây?
A. 11 m/s
B. 12 m/s
C. 13 m/s
D. 14 m/s
Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức ?
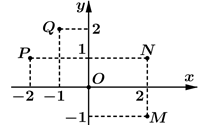
A. N
B. P
C. M
D. Q
Cho hai số phức và . Môđun của số phức bằng
A.
B.
C.
D.
Cho hai số phức và . Biết , tính
A. S = -1
B. S = 4035
C. S = -2019
D. S = -2016
Xét các số phức z thỏa mãn là số thuần ảo. Biết rằng tập hợp tất cả các điểm biễu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là
A. (1;-1)
B. (1;1)
C. (-1;1)
D. (-1;-1)
Trong khai triển nhị thức Niutơn của có tất cả 2019 số hạng . Khi đó giá trị n bằng
A. 2012
B. 2013
C. 2018
D. 2019
Tìm số nguyên dương n thỏa mãn
A. n = 5
B. n = 7
C. n = 8
D. n = 10
Có bốn đội tuyển gồm Việt Nam, Malaysia, Thái Lan, Philippnes. Mỗi đội có 2 cầu thủ xuất sắc. Hỏi có bao nhiêu cách chọn ra 3 cầu thủ từ 8 cầu thủ sao cho 3 cầu thủ ở ba đội khác nhau?
A. 4
B. 24
C. 32
D. 56
Cho cấp số cộng có công sai . Khi đó dãy số
A. Không là cấp số cộng
B. Là cấp số cộng với công sai 4d
C. Là cấp số nhân với công bội d
D. Là cấp số nhân với công bội 4d
Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo quý với phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là: và kể từ quý làm việc thứ hai mức lương sẽ được tăng thêm 1,5 triệu đồng cho mỗi quý so với quý trước. Tổng số tiền lương một kỹ sư được nhận sau 2 năm làm việc cho công ty là
A. 122 triệu
B. 123 triệu
C. 128 triệu
D. 164 triệu
Kết quả của giới hạn là
A.
B.
C. 1
D.
Cho hàm số có đồ thị (C). Có bao nhiêu điểm thuộc (C) mà tiếp tuyến của (C) tại điểm đó cắt trục tọa độ Ox, Oy lần lượt tại A, B thỏa ?
A. 1
B. 2
C. 3
D. 4
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, N lần lượt là trung điểm của SA, SC (tham khảo hình vẽ). Tìm giao tuyến d của hai mặt phẳng (BIN) và (ABCD)
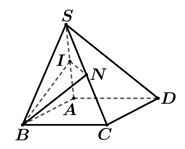
A. d là đường thẳng đi qua B và song song với AC
B. d là đường thẳng đi qua S và song song với AD
C. d là đường thẳng đi qua B và song song với CD
D. d là đường thẳng đi qua hai điểm I, N
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai mặt phẳng (A'B'CD) và (ABC'D') bằng
A. 30
B. 60
C. 45
D. 90
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với . Cạnh bên SA vuông góc với đáy, SB hợp với đáy góc . Khoảng cách giữa hai đường thẳng AD và SC bằng
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với . Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SAD) bằng
A. 30
B. 45
C. 60
D. 90
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC = 2a, BC = a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng . Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A.
B.
C.
D.
Hình đa diện nào dưới đây không có tâm đối xứng?

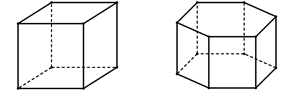
A. Tứ diện đều
B. Bát diện đều.
C. Hình lập phương
D. Lăng trụ lục giác đều.
Cho hình chóp S.ABC có tam giác ABC là tam giác vuông cân tại S, SB = 2a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC
A.
B.
C.
D.
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2;-1;3), B(-10;5;3) và M(2m-1;2;n+2). Để A, B, M thẳng hàng thì giá trị của m, n là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có bán kính bằng 2 tiếp xúc với mặt phẳng (Oyz) và có tâm nằm trên tia Ox. Phương trình của mặt cầu (S) là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho hai điểm P(2;0;-1), Q(1;-1;3) và mặt phẳng . Gọi là mặt phẳng đi qua P, Q và vuông góc với (P), phương trình của mặt phẳng là
A. : -7x + 11y + z - 3 = 0
B. : 7x - 11y + z - 1 = 0
C. : -7x + 11y + z + 15 = 0
D. : 7x - 11y - z + 1 = 0
Trong không gian với hệ tọa độ Oxyz cho mặt cầu và mặt phẳng . Khoảng cách ngắn nhất giữa điểm (M) trên (S) và điểm N trên (P) bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz tính khoảng cách d từ điểm M(1;3;2) đến đường thẳng
A.
B. d = 2
C.
D. d = 3
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;2;3) và mặt phẳng . Đường thẳng d đi qua điểm A song song với mặt phẳng (P), đồng thời cắt trục Oz. Phương trình tham số của đường thẳng d là
A.
B.
C.
D.
Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên. Hàm số đồng biến trên khoảng nào trong các khoảng sau ?

A. (-1;0)
B.
C. (0;1)
D.
Cho hàm số y = f(x) có đạo hàm trên . Đồ thị hàm số như hình vẽ bên. Số điểm cực trị của hàm số là
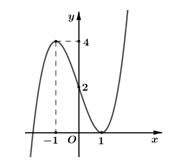
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = f(x) liên tục và có đạo hàm trên , có đồ thị như hình vẽ. Với m là tham số bất kì thuộc [0;1]. Phương trình có bao nhiêu nghiệm thực?
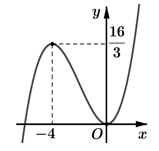
A. 2
B. 3
C. 5
D. 9
Cho các số thực dương a, b, c thỏa mãn . Giá trị lớn nhất của biểu thức bằng
A.
B.
C.
D.
Cho hàm số y = f(x) xác định và liên tục trên đoạn [-3;3] và có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và đường thẳng lần lượt là M;m. Tích phân bằng
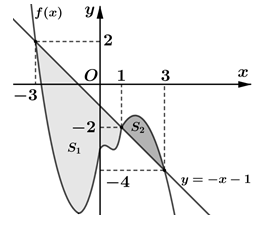
A. 6+m-M
B. 6-m-M
C. M-m+6
D. m-M-6
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình có đúng 6 nghiệm phân biệt thuộc đoạn là
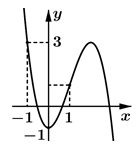
A. 1
B. 2
C. 3
D. 5
Một hộp chứa 6 quả bóng đỏ (được đánh số từ 1 đến 6), 5 quả bóng vàng (được đánh số từ 1 đến 5), 4 quả bóng xanh (được đánh số từ 1 đến 4). Lấy ngẫu nhiên 4 quả bóng. Xác suất để 4 quả bóng lấy ra có đủ ba màu mà không có hai quả bóng nào có số thứ tự trùng nhau bằng
A.
B.
C.
D.
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a chiều cao bằng 2a. Mặt phẳng (P) qua B' và vuông góc A'C chia lăng trụ thành hai khối. Biết thể tích của hai khối là và với . Tỉ số bằng
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ tam giác đều có . hai đỉnh B, C thuộc trục Oz và (C không trùng O). Biết là một vectơ chỉ phương của đường thẳng . Tính
A. T = 4
B. T = 5
C. T = 9
D. T = 16