Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 9)
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Hàm số có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số ?
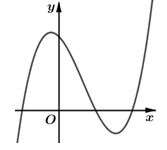
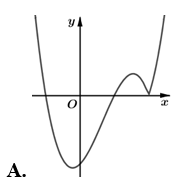

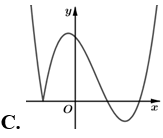
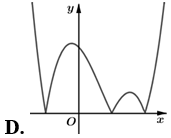
Cho hàm số có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
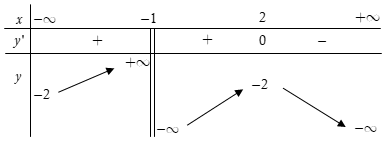
A. Hàm số đã cho đồng biến trên các khoảng và
B. Hàm số đã cho đồng biến trên
C. Hàm số đã cho đồng biến trên khoảng (0;2)
D. Hàm số đã cho đồng biến trên (-2;2)
Cho hàm số xác định, liên tục trên đoạn và có đồ thị là đường cong trong hình vẽ bên. Hàm số đạt cực đại tại điểm nào dưới đây?
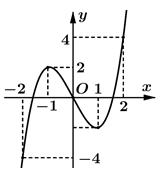
A. x = -2
B. x = -1
C. x = 1
D. x = 2
Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
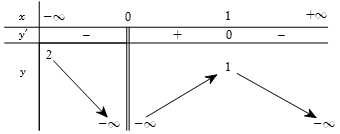
A. 1
B. 2
C. 3
D. 4
Cho a, b là các số thực dương khác 1. Các hàm số và có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số , , trục tung lần lượt tại M, N, A đều thỏa mãn AN = 2AM. Mệnh đề nào sau đây đúng?
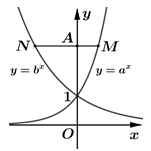
A. b = 2a
B.
C.
D.
Cho x > 0 và số thực y thỏa mãn . Giá trị của biểu thức bằng
A. 1
B. 2
C. 3
D. 4
Tìm tập nghiệm S của phương trình
A. S = {3}
B.
C.
D.
Tìm tập nghiệm S của bất phương trình
A. S = [2;16]
B.
C.
D.
Đúng ngày 01 mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất . Biết không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng tiền lãi sẽ nhập vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng thì anh A có được số tiền cả gốc và lãi nhiều hơn 100 triệu đồng? Giả định trong suốt thời gian gửi, lãi suất không đổi, được tính lãi ngay từ ngày gửi và anh A không rút tiền ra.
A. 28 thángc
B. 29 tháng
C. 30 tháng
D. 33 tháng
Nguyên hàm của hàm số là
A.
B.
C.
D.
Cho tích phân và . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi cung tròn , trục hoành (tham khảo hình) xung quanh trục hoành là
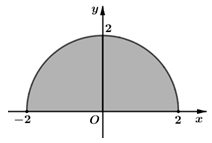
A.
B.
C.
D.
Biết rằng đường Parabol chia đường tròn thành hai phần lần lượt có diện tích là (hình bên). Khi đó với a, b, c nguyên dương và là phân số tối giản. Tổng bằng
A. 13
B. 14
C. 15
D. 16
Một vật chuyển động trong 4 giờ với vận tốc phụ thuộc thời gian có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường Parabol có đỉnh I(2;9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đuờng s mà vật chuyển động trong 4 giờ đó.
A. s = 24 km
B. s = 26,5 km
C. s = 27 km
D. s = 28,5 km
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là
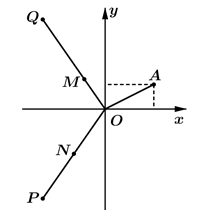
A. Điểm Q
B. Điểm M
C. Điểm N
D. Điểm P
Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức . Khẳng định nào sau đây là đúng?
A. a = 1, b = 1
B. a = 1, b = 1
C. a = 1, c = -1
D. a = 1, b = -i
Nếu là một nghiệm phức của phương trình với thì bằng
A. -2
B. -1
C. 1
D. 2
Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn của số phức thỏa mãn là
A. Đường tròn tâm O bán kính
B. Đường tròn đường kính AB với và
C. Đường trung trực của đoạn thẳng AB với và
D. Đường thẳng vuông góc với đoạn AB tại A với A
Tính tổng S tất cả các hệ số trong khai triển
A. S = 1
B. S = -1
C. S = 0
D. S = 8192
Có bao nhiêu số tự nhiên n thỏa mãn ?
A. 1
B. 2
C. 3
D. Vô số
Ba người cùng bắn vào một bia một cách độc lập. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,5; 0,6; và 0,8 Xác suất để có đúng 2 người bắn trúng đích là
A. 0,24
B. 0,46
C. 0,92
D. 0,96
Nếu cấp số cộng có công sai là d thì dãy số với là một cấp số cộng có công sai là
A. d - 13
B. d + 13
C. d
D. 13d
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng bằng nửa diện tích của đế tháp (có diện tích là ). Diện tích mặt trên cùng (tầng thứ 11) bằng
A. 6
B. 8
C. 10
D. 12
Giá trị của là
A. 0
B.
C.
D.
Cho hàm số xác định, có đạo hàm liên tục trên , thỏa mãn với mọi . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục tung.
A. y = 2 - x
B. y = -x
C. y = x
D. y = 2x - 1
Cho tứ diện ABCD. Gọi và lần lượt là trọng tâm các tam giác BCD và ACD. Khẳng định nào sau đây là sai?
A. //(ABD)
B. //(ABC)
C. B, Avà CD đồng quy
D.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và . Gọi M là trung điểm của BC. Góc giữa hai đường thẳng OM và AB bằng
A. 30
B. 45
C. 60
D. 90
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với . Cạnh bên SA vuông góc với đáy, góc giữa SD với đáy bằng . Khoảng cách từ điểm C đến mặt phẳng (SBD) bằng
A.
B.
C.
D.
Cho hình lập phương . Gọi M là trung điểm của AD và là góc giữa hai mặt phẳng (BMC') và (ABB'A'). Khẳng định nào dưới dây đúng?
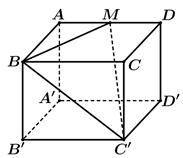
A.
B.
C.
D.
Cho hình lăng trụ có đáy là tam giác đều cạnh có độ dài bằng 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của BC. Khoảng cách giữa hai đường thẳng BB' và A'H bằng
A.
B.
C. a
D. 2a
Mặt phẳng chia khối lăng trụ thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Cho hình chóp có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng . Thể tích khối chóp đã cho bằng
A.
B.
C.
D.
Hình nón có góc ở đỉnh bằng và chiều cao bằng . Độ dài đường sinh của hình nón bằng
A. 2
B.
C.
D. 3
Công ty của ông Bình dự định đóng một thùng phi hình trụ (có đáy dưới và nắp đậy phía trên) bằng thép không rỉ để đựng nước. Chi phí trung bình cho thép không rỉ là 350000 đồng. Với chi phí không quá 6594000 đồng, hỏi công ty ông Bình có thể có được một thùng phi đựng được tối đa bao nhiêu tấn nước? (Lấy )
A. 3,14
B. 6,28
C. 12,56
D. 9,52
Trong không gian với hệ tọa độ Oxyz cho bốn điểm và . Hệ thức giữa m và p để bốn điểm A, B, C, D đồng phẳng là
A. 2m + p = 0
B. m + p = 1
C. m + 2p = 3
D. 2m - 3p = 0
Trong không gian với hệ tọa độ Oxyz cho là phương trình mặt cầu và là phương trình mặt phẳng. Tìm tất cả các giá trị thực của m để mặt cầu (P) và mặt phẳng có điểm chung.
A. m > 3; m < 2
B.
C.
D. m > 9; m < -5
Trong không gian với hệ tọa độ Oxyz cho là phương trình mặt cầu, điểm và đường thẳng . Tìm tọa độ điểm M thuộc d, N thuộc (S) sao cho I là trung điểm MN.
A. N(3;2;1); N(3;6;-1)
B. N(-3;-2;1); N(3;6;-1)
C. N(-3;2;1); N(3;6;1)
D. N(-3;-2;1); N(3;6;1)
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng . Tìm mệnh đề đúng trong các mệnh đề sau
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho đường thẳng . Xét mặt phẳng với m là tham số thực. Tìm giá trị của m để mặt phẳng (P) vuông góc với đường thẳng
A. m = -2
B. m = 2
C. m = -52
D. m = 52
Trong không gian với hệ tọa độ Oxzyz cho đường thẳng và mặt phẳng . Góc hợp bởi giữa đường thẳng d và mặt phẳng (P) bằng
A. 30
B. 45
C. 60
D. 90
Cho hàm số . Đồ thị hàm số như hình bên và . Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
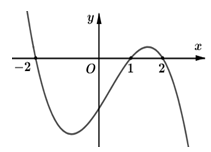
A. (-2;-1)
B. (1;2)
C. (2;5)
D.
Cho hàm số có bảng biến thiên như sau
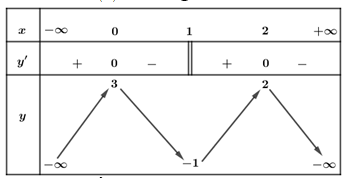
Số điểm cực trị của hàm số là
A. 2
B. 3
C. 5
D. 6
Cho hàm bậc ba có đồ thị như hình. Đồ thị hàm số có bao nhiêu đường tiệm cận đứng ?
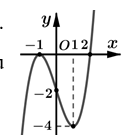
A. 1
B. 2
C. 3
D. 4
Cho hàm số . Có bảng xét dấu đạo hàm như sau
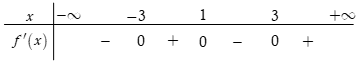
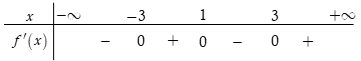
Bất phương trình đúng với mọi khi chỉ khi
A.
B.
C.
D.
Cho x, y là các số thực thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
A.
B.
C. -2
D. -1
Cho hàm số có đạo hàm và liên tục trên , thỏa mãn và . Tính
A.
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để phương trình có 12 nghiệm phân biệt thuộc đoạn ?
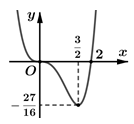
A. 2
B. 3
C. 4
D. 5
Cho tập hợp . Gọi S là tập hợp các số tự nhiên có 4 chữ số được lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi là góc giữa hai mặt phẳng (SBC) và (ABC), tính khi thể tích khối chóp nhỏ nhất.
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, xét đường thẳng đi qua điểm và vuông góc với mặt phẳng . Tính khoảng cách nhỏ nhất giữa điểm tới điểm C trong đó C là điểm cách đều đường thẳng và trục Ox.
A.
B.
C.
D.