ĐỀ THỬ SỨC SỐ 1
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2.
A. Đường thẳng
B. Đường thẳng
C. Đường thẳng
D. Đường thẳng
Trong không gian Oxyz tính khoảng cách d giữa hai mặt phẳng cho bởi các phương trình và .
A.
B.
C.
D.
Đẳng thức nào dưới đây không đúng với mọi ?
A.
B.
C.
D.
Gieo một con súc sắc cân đối và đồng chất. Giả sử con súc sắc xuất hiện mặt b chấm. Tính xác suất sao cho phương trình (x là ẩn số) có nghiệm lớn hơn 3.
A.
B.
C.
D.
Trong các dãy số có số hạng tổng quát dưới đây, dãy số nào là dãy giảm?
A.
B.
C.
D.
Trong các giới hạn hữu hạn sau, giới hạn nào có giá trị khác với các giới hạn còn lại?
A.
B.
C.
D.
Tìm tất cả các giá trị thực của tham số a sao cho hai đường thẳng sau đây cắt nhau. và
A.
B. a=-1
C. a=1
D.
Có bao nhiêu cách chọn ra 4 bóng đèn từ 6 bóng đèn khác nhau rồi mắc nối tiếp chúng?
A. 24
B. 15
C. 30
D. 360
Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số . Mệnh đề nào dưới đây đúng?
A. d song song với đường thẳng x=3
B. d song song với đường thẳng y=3
C. d có hệ số góc âm
D. d có hệ số góc dương
Trong không gian Oxyz cho điểm . Viết phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trọng tâm của tam giác ABC.
A.
B.
C.
D.
Cho hàm số . Mệnh đề nào dưới đây đúng?
A. Hàm số f(x) đồng biến trên R
B. Hàm số f(x) nghịch biến trên R
C. Hàm số đồng biến trên và nghịch biến trên
D. Hàm số nghịch biến trên và đồng biến trên
Mệnh đề nào dưới đây sai?
A. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau
B. Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau
C. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau
D. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau
Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính thể tích của khối trụ đó.
A.
B.
C.
D.
Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Tính
A.
B.
C.
D.
Cho mặt cầu (S) có phương trình và mặt phẳng có phương trình . Tính bán kính của đường tròn (c) là giao tuyến của mặt phẳng và mặt cầu (S)
A. 8
B.
C. 10
D. 6
Tìm tất cả các giá trị thực của tham số m để hàm số xác định với mọi .
A.
B.
C.
D.
Cho hàm số có đồ thị là đường gấp khúc như hình vẽ bên. Tính .
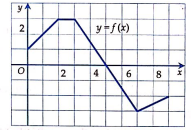
A. 18
B. 2
C. 0
D. 16
Mệnh đề nào dưới đây đúng?
A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c.
B. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c.
C. Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c.
D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a;b).
Đồ thị hàm số nào dưới đây không có tiệm cận ngang?
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm , bán kính . Viết phương trình đường tròn là ảnh của đường tròn qua phép vị tự tâm O, tỉ số .
A.
B.
C.
D.
Mệnh đề nào dưới đây sai?
A. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
C. Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
D. Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại.
Một đoàn tàu được ghép bởi bốn toa tàu A, B, C, D và được kéo bởi một đầu máy. Có bao nhiêu cách sắp xếp các toa tàu sao cho toa A gần đầu máy hơn toa B?
A. 4
B. 12
C. 24
D. 6
Cho hình lăng trụ tam giác . Gọi I, J lần lượt là trọng tâm của các tam giác ABC và . Thiết diện tạo bởi mặt phẳng với hình lăng trụ đã cho là hình gì?
A. Tam giác cân
B. Tam giác vuông
C. Hình thang
D. Hình bình hành
Cho hai số thực dương a và b. Rút gọn biểu thức .
A.
B.
C.
D.
Cho . Tính .
A. 7
B. 3
C. 0
D. ‒3
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng . Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.
A.
B.
C.
D. 3
Tính tổng các nghiệm trong khoảng của phương trình .
A. ‒2
B. 0
C. 2
D.
Tính khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh a.
A.
B.
C.
D.
Cho . Biết , tính theo .
A.
B.
C.
D.
Biết . Tính .
A. 1
B. ‒1
C.
D.
Cho hình lập phương . Gọi là hình bát diện đều có các đỉnh là tâm các mặt của . Tính tỉ số thể tích của và .
A.
B.
C.
D.
Cho số phức . Tìm phương trình bậc hai nhận và làm nghiệm.
A.
B.
C.
D.
Trong không gian Oxyz, viết phương trình đường thẳng song song với trục Oz và cắt hai đường thẳng ; .
A.
B.
C.
D.
Tìm phần nguyên của nghiệm lớn nhất trong khoảng của phương trình .
A.
B.
C. ‒6
D. ‒7
Trong mặt phẳng có m đường thẳng song song với nhau và n đường thẳng vuông góc với m đường thẳng song song đó (). Có nhiều nhất bao nhiêu hình chữ nhật được tạo thành từ các đường thẳng đó nếu ?
A. 588
B. 586
C. 584
D. 582
Trong không gian Oxyz cho tứ diện ABCD có thể tích , các đỉnh , , đỉnh thứ tư D nằm trên trục Oy và có tung độ dương. Tìm tọa độ của D.
A.
B.
C.
D.
Gọi S là diện tích của hình phẳng giới hạn bởi parabol và đường tròn có tâm tại gốc tọa độ, bán kính bằng . Biết , trong đó . Tính tổng .
A. 6
B. 7
C. 8
D. 9
Cho m và n là các số nguyên. Biết hàm số có các cực trị đều là những số dương và một điểm cực trị . Tìm giá trị nhỏ nhất của .
A. ‒1
B. 0
C. 8
D. 1
Cho hàm số và điểm . Gọi S là tập hợp tất cả các giá trị thực của m sao cho có đúng một tiếp tuyến của đồ thị hàm số đi qua A. Biết S là hợp của một số khoảng rời nhau. Có bao nhiêu khoảng như vậy?
A. 4
B. 3
C. 2
D. 1
Tìm tất cả các giá trị thực của tham số m để hàm số có với mọi .
A.
B.
C.
D.
Cho một tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng a . Tìm theo a giá trị lớn nhất của diện tích của tam giác vuông đó.
A.
B.
C.
D.
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Giả sử hàm chỉ mức mức sản xuất của một hãng DVD trong một ngày là , trong đó m là số lượng nhân viên và n là số lượng lao động chính. Mỗi ngày hãng phải sản xuất được ít nhất 40 sản phẩm để đáp ứng nhu cầu của khách hàng. Biết rằng tiền lương một ngày cho một nhân viên là 16 USD và cho một lao động chính là 27 USD. Tìm giá trị nhỏ nhất của chi phí trong một ngày của hãng sản xuất này.
A. 1446 USD
B. 1440 USD
C. 1908 USD
D. 1892 USD
Cho hàm số có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số ?

A.
B.
C.
D.
Cho hình lăng trụ đứng tam giác có tất cả các cạnh đều bằng a. Mặt phẳng đi qua và trọng tâm tam giác ABC cắt AC và BC lần lượt tại E và F. Tính thể tích V của khối chóp .
A.
B.
C.
D.
Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức , trong đó .
A. Hình tròn tâm bán kính .
B. Đường tròn tâm bán kính .
C. Hình tròn tâm bán kính .
D. Đường tròn tâm bán kính .
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C, .
A.
B.
C.
D.
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi, ( R>0 ). Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.

A.
B.
C.
D.
Một hình hộp chữ nhật có kích thước chứa một khối cầu bán kính bằng 2 và tám khối cầu nhỏ hơn có bán kính bằng 1. Các khối cầu nhỏ đôi một tiếp xúc nhau và tiếp xúc với ba mặt của hình hộp, khối cầu lớn tiếp xúc với cả tám khối cầu nhỏ (xem hình vẽ). Tìm giá trị của h.
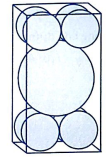
A.
B.
C.
D.