ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bài toán về đồ thị hàm số bậc hai
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho đồ thị hàm số \[y = a{x^2} + bx + c\] như hình vẽ.
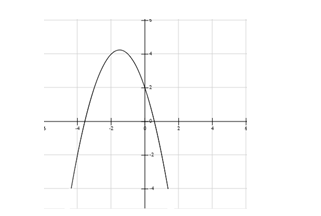
Khẳng định nào sau đây là đúng:
A.a >0, b < 0, c >0
B. a < 0, b >0,c >0
C. a < 0, b < 0, c < 0
D. a < 0, b < 0, c >0
Xác định Parabol (P):\[y = a{x^2} + bx + 2\;\] biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
A.\[y = - 5{x^2} + 8x + 2\]
B. \[y = 10{x^2} + 13x + 2\]
C. \[y = - 10{x^2} - 13x + 2\]
D. \[y = 9{x^2} + 6x - 5\]
Xác định Parabol (P):\[y = a{x^2} + bx - 5\] biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
A.\[y = \frac{1}{{18}}{x^2} + \frac{1}{6}x - 5\]
B. \[y = \frac{1}{{18}}{x^2} + \frac{1}{6}x + 5\]
C. \[y = 3{x^2} + 9x - 9\]
D. \[y = - \frac{1}{{18}}{x^2} + \frac{1}{6}x - 5\]
Xác định Parabol (P):\[y = a{x^2} + bx + 3\;\] biết rằng Parabol có đỉnh I(3;−2).
A.\[y = {x^2} - 6x + 3\]
B. \[y = - \frac{5}{9}{x^2} + \frac{{10}}{3}x + 3\]
C. \[y = 3{x^2} + 9x + 3\]
D. \[y = \frac{5}{9}{x^2} - \frac{{10}}{3}x + 3\]
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
A.\(\)\[y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x - 2\]
B. \[y = \frac{7}{{10}}{x^2} - \frac{1}{{10}}x + 2\]
C. \[y = \frac{7}{{10}}{x^2} - \frac{1}{{10}}x - 2\]
D. \[y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x + 2\]
Tìm các giá trị của tham số m để phương trình \[2{x^2} - 2x + 1 - m = 0\;\]có hai nghiệm phân biệt
A.\[m >\frac{1}{2}\]
B. \[m = \frac{1}{2}\]
C. \[m < \frac{1}{2}\]
D. Không tồn tại
Tìm các giá trị thực của tham số m để phương trình \[\left| {{x^2} - 3x + 2} \right| = m\;\] có bốn nghiệm thực phân biệt.
A.\[m \ge \frac{1}{4}\]
B. \[0 < m < \frac{1}{4}\]
C. \(m = 0\)
D. Không tồn tại
Tìm các giá trị của tham số m để phương trình \[\frac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}\] có 3 nghiệm thực phân biệt.
A.m = 3
B.\[ - \sqrt 3 < m < \sqrt 3 \]
C. \[m = \pm \sqrt 3 \]
D. Không tồn tại
Tìm các giá trị của m để phương trình \[{x^2} - 2x + \sqrt {4{x^2} - 12x + 9} = m\] có nghiệm duy nhất.
A.\[ - \frac{3}{4} < m < 0\]
B. \[ - \frac{{\sqrt 3 }}{2} < m < \frac{{\sqrt 3 }}{2}\]
C. \[m = - \frac{3}{4}\]
D. Không tồn tại
Cho phương trình của (P):\[y = a{x^2} + bx + c\left( {a \ne 0} \right)\] biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tình tổng \[{a^2} + {b^2} + {c^2}\]
A.\[{a^2} + {b^2} + {c^2} = 3\]
B. \[{a^2} + {b^2} + {c^2} = \frac{{29}}{{16}}\]
C. \[{a^2} + {b^2} + {c^2} = \frac{{48}}{{29}}\]
D. \(\left[ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2} = 5}\\{{a^2} + {b^2} + {c^2} = \frac{{209}}{{16}}}\end{array}} \right.\)
Biết đồ thị hàm số (P):\[y = {x^2} - ({m^2} + 1)x - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ x1,x2. Tìm giá trị của tham số mm để biểu thức \[T = {x_1} + {x_2}\;\] đạt giá trị nhỏ nhất.
A.m >0
B. m < 0
C. m = 0
D.Không xác định được
Tìm các giá trị của tham số mm để phương trình \[{x^2} - 2(m + 1)x + 1 = 0\;\] có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).
A. m >0
B. m < 0
C. m = 0
D.Không xác định được
Tìm các giá trị của tham số m để \[2{x^2} - 2(m + 1)x + {m^2} - 2m + 4 \ge 0(\forall x)\]
A. m = 3
B. \[3 - \sqrt 2 < m < 3 + \sqrt 2 \]
C. \[\left[ {\begin{array}{*{20}{c}}{m \ge 3 + \sqrt 2 }\\{m \le 3 - \sqrt 2 }\end{array}} \right.\]
D. Không tồn tại
Tìm giá trị nhỏ nhất của hàm số f(x) biết rằng \[f(x + 2) = {x^2} - 3x + 2\;\] trên \(\mathbb{R}\)
A.\[ - \frac{1}{4}\]
B. \[\frac{1}{4}\]
C. \(\frac{1}{2}\)
D. 0
Cho hàm số \[f(x) = {x^2} + 2x - 3\].
Xét các mệnh đề sau:
i) \[f(x - 1) = {x^2} - 4\]
ii) Hàm số đã cho đồng biến trên \[\left( { - 1; + \infty } \right)\]
iii) Giá trị nhỏ nhất của hàm số là một số âm.
iv) Phương trình \[f(x) = m\;\] có nghiệm khi \[m \ge - 4\]
Số mệnh đề đúng là:
A.1
B.2
C.3
D.4
Tìm các giá trị của m để hàm số \[y = {x^2} + mx + 5\;\] luôn đồng biến trên \[\left( {1; + \infty } \right)\]
A. m < −2
B. m ≥ −2
C. m = −4
D.Không xác định được
Tìm giá trị của m để hàm số \[y = - {x^2} + 2x + m - 5\] đạt giá trị lớn nhất bằng 6
A. m = 0
B. m = 10
C. m = −10
D.Không xác định được
Tìm giá trị của m để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
A.\(\left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 2}\end{array}} \right.\)
B. \(\left[ {\begin{array}{*{20}{c}}{m < 1}\\{m >2}\end{array}} \right.\)
C. 1 < m < 2
D. Không xác định được
Tìm điểm A cố định mà họ đồ thị hàm số \[y = {x^2} + (2 - m)x + 3m\,\,\,\,\,\,\,\,\,\,({P_m})\;\] luôn đi qua.
A.A(3;15)
B.A(0;−2)
C.A(3;−15)
D.A(−3;−15)
Tìm giá trị nhỏ nhất của biểu thức \[P = 3\left( {\frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\frac{a}{b} + \frac{b}{a}} \right)\].
A.\[ - \frac{{34}}{3}\]
B.4
C.22
D.−10
Một chiếc cổng parabol dạng \[y = - 12{x^2}\;\] có chiều rộng d = 8m. Hãy tính chiều cao h của cổng ?
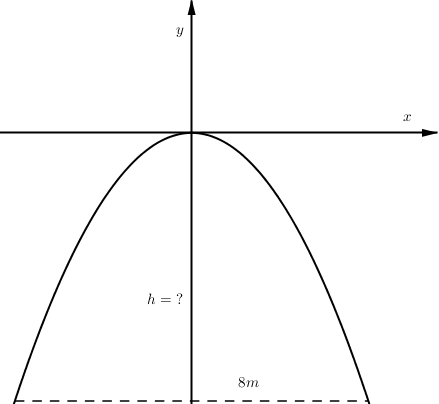
A. h = 8m.
B. h = 7m.
C. h = 9m.
D. h = 5m.