ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Giới hạn của dãy số
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Dãy số nào sau đây có giới hạn 0?
A.\[{u_n} = \frac{n}{2}\]
B. \[{u_n} = \frac{2}{n}\]
C. \[{u_n} = n\]
D. \[{u_n} = \sqrt n \]
Biết \[\lim {u_n} = 3\]. Chọn mệnh đề đúng trong các mệnh đề sau.
A.\[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 3\]
B. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = - 1\]
C. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 2\]
D. \[\lim \frac{{3{u_n} - 1}}{{{u_n} + 1}} = 1\]
Dãy số nào dưới đây không có giới hạn 0?
A.\[{u_n} = \frac{1}{{\sqrt n }}\]
B. \[{u_n} = \frac{1}{{\sqrt[3]{n}}}\]
C. \[{u_n} = \frac{{\sqrt[3]{n}}}{2}\]
D. \[{u_n} = 0\]
Cho hai dãy số \[\left( {{u_n}} \right),\left( {{v_n}} \right)\]thỏa mãn \[\left| {{u_n}} \right| \le {v_n}\] với mọi n và \[\lim {u_n} = 0\] thì:
A.\[\lim {u_n} = 0\]
B. \[\lim {u_n} >\lim {v_n}\]
C. \[\lim {u_n} < \lim {v_n}\]
D. \[\lim {u_n} < 0\]
Cho \[n \in {N^ * }\] nếu \[|q| < 1\;\]thì:
A.\[\lim {q^n} = 0\]
B. \[\lim q = 0\]
C. \[\lim \left( {n.q} \right) = 0\]
D. \[\lim \frac{n}{q} = 0\]
Dãy số (un) có giới hạn là số thực L nếu:
A.\[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - L} \right) = 0\]
B. \[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}} \right) = 0\]
C. \[\mathop {\lim }\limits_{n \to + \infty } L = 0\]
D. \[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + L} \right) = 0\]
Giả sử \[\lim {u_n} = L\]. Khi đó:
A.\[\lim \left| {{u_n}} \right| = L\]
B. \[\lim \left| {{u_n}} \right| = - L\]
C. \[\lim {u_n} = \left| L \right|\]
D. \[\lim \left| {{u_n}} \right| = \left| L \right|\]
Cho \[\lim {u_n} = L\]. Chọn mệnh đề đúng:
A.\[\lim \sqrt[3]{{{u_n}}} = L\]
B. \[\lim \sqrt {{u_n}} = L\]
C. \[\lim \sqrt {{u_n}} = \sqrt L \]
D. \[\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\]
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\]. Chọn mệnh đề đúng:
A.\[\lim \left( {{u_n} + {v_n}} \right) = L + M\]
B. \[\lim \left( {{u_n} + {v_n}} \right) = L - M\]
C. \[\lim \left( {{u_n} - {v_n}} \right) = L + M\]
D. \[\lim \left( {{u_n} - {v_n}} \right) = L.M\]
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\] và c là một hằng số. Chọn mệnh đề sai:
A.\[\lim \left( {{u_n} - {v_n}} \right) = L - M\]
B. \[\lim \left( {{u_n} + {v_n}} \right) = L + M\]
C. \[\lim \left( {{u_n}.{v_n}} \right) = L.M\]
D. \[\lim \left( {c{u_n}} \right) = cM\]
Cho cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\]công bội q. Đặt \[S = {u_1} + {u_2} + ... + {u_n} + ...\] thì:
A.\[S = \frac{{{u_1}}}{{1 - q}}\]
B. \[S = \frac{{{u_1}}}{{q - 1}}\]
C. \[S = \frac{{1 - q}}{{{u_n}}}\]
D. \[S = \frac{{{u_1}}}{{1 - {q^n}}}\]
Chọn mệnh đề sai:
A.\[\lim n = + \infty \]
B. \[\lim \sqrt n = + \infty \]
C. \[\lim \sqrt[3]{n} = + \infty \]
D. \[\lim \frac{1}{n} = + \infty \]
Cho các dãy số \[{u_n} = \frac{1}{n},n \ge 1\]và \({v_n} = {n^2},n \ge 1\). Khi đó:
A.\[\lim \left( {{u_n}.{v_n}} \right) = 0\]
B. \[\lim \left( {{u_n}.{v_n}} \right) = + \infty \]
C. \[\lim \left( {{u_n}.{v_n}} \right) = - \infty \]
D. \[\lim \left( {{u_n}.{v_n}} \right) = 1\]
Trong các khẳng định sau, khẳng định nào sai:
A.\[\lim {(\sqrt 2 )^n} = 0\]
B. \[\lim {\left( {\frac{1}{3}} \right)^n} = 0\]
C. \[\lim {\left( {\frac{1}{{\sqrt 2 }}} \right)^n} = 0\]
D. \[\lim {\left( {\frac{1}{{\sqrt 3 }}} \right)^n} = 0\]
Gọi S là tổng của cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\;\]có công bội \[q\left( {\left| q \right| < 1} \right)\]. Khẳng định nào sau đây đúng ?
A.\[S = \frac{{{u_1}}}{{1 - q}}\]
B. \[S = \frac{{{u_1}}}{{1 + q}}\]
C. \[S = \frac{1}{{{u_1} - q}}\]
D. \[S = \frac{{{u_1}}}{{q - 1}}\]
Cho \[{u_n} = \frac{{1 - 4n}}{{5n}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.\[\frac{1}{5}.\]
B. \[ - \frac{4}{5}.\]
C. \[\frac{4}{5}.\]
D. \[ - \frac{1}{5}.\]
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.\(0\)
B. \[ - \frac{1}{4}.\]
C. \[\frac{3}{4}.\]
D. \[ - \frac{3}{4}.\]
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A..0.
B.\[ - \frac{1}{4}.\]
C. \[\frac{3}{4}.\]
D. \[ - \frac{3}{4}.\]
Cho \[{u_n} = \frac{{{3^n} + {5^n}}}{{{5^n}}}\]. Khi đó \[lim\,{u_n}\]bằng?
A.0.
B.1.
C.\[\frac{3}{5}.\]
D. \[ + \infty .\]
Trong các giới hạn sau giới hạn nào bằng −1?
A.\[\lim \frac{{2{n^2} - 3}}{{ - 2{n^3} - 4}}.\]
B. \[\lim \frac{{2{n^2} - 3}}{{ - 2{n^2} - 1}}.\]
C. \[\lim \frac{{2{n^2} - 3}}{{2{n^2} + 1}}.\]
D. \[\lim \frac{{2{n^3} - 3}}{{2{n^2} - 1}}.\]
Giá trị \[\lim \left( {{n^3} - 2n + 1} \right)\] bằng
A.0
B.1
C.\[ - \infty \]
D. \[ + \infty \]
Giới hạn \[\lim \frac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}\] bằng?
A.1.
B.\[\frac{2}{3}.\]
C. -1
D. \[ - \frac{1}{3}.\]
Giới hạn \[\lim \frac{{{{\left( {2 - 5n} \right)}^3}{{\left( {n + 1} \right)}^2}}}{{2 - 25{n^5}}}\] bằng?
A.−4.
B.−1.
C.5.
D.\[ - \frac{3}{2}.\]
Giới hạn \[\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}\] bằng?
A.\[\frac{5}{2}.\]
B. \[\frac{{ - 5}}{2}.\]
C. 1
D. -1
Giới hạn \[\lim \frac{{2{n^2} - n + 4}}{{\sqrt {2{n^4} - {n^2} + 1} }}\] bằng?
A.1.
B.\(\sqrt 2 \)
C. 2
D. \[\frac{1}{{\sqrt 2 }}.\]
Giới hạn \[\lim \left( {\sqrt {{n^2} - n} - n} \right)\] bằng?
A.\[ - \infty .\]
B. \( - \frac{1}{2}\)
C. 0
D. \[ + \infty .\]
Giới hạn \[\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)\] bằng?
A..0.
B.\( - \frac{1}{2}\)
C. \[ - \frac{1}{{\sqrt 2 }}.\]
D. \[\frac{1}{{\sqrt 2 }}.\]
Cho dãy số \[\left( {{u_n}} \right)\]với \[{u_n} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + .... + \frac{1}{n} - \frac{1}{{n + 1}}\]. Khi đó \[lim\,{u_n}\] bằng?
A.0.
B.\(\frac{1}{2}\)
C. 1
D. 2
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{1}{{1.3}} + \frac{1}{{3.5}} + ... + \frac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}\]
Khi đó \[lim\,{u_n}\] bằng?
A.\(\frac{1}{2}\)
B. \[\frac{1}{4}.\]
C. 1
D. 2
Giá trị \[\lim \frac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}\] bằng
A.0.
B.1.
C.\[ + \infty .\]
D. 2
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}\] Khi đó \[lim\,{u_n}\] bằng?
A.\[ - \infty .\]
B. -1
C. \[ + \infty .\]
D. \[\frac{{ - 2}}{5}.\]
Cho dãy số \[({u_n})\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 2}\\{{u_{n + 1}} = \frac{{{u_n} + 1}}{2},\left( {n \ge 1} \right)}\end{array}} \right.\) Khi đó mệnh đề nào sau đây là đúng?
A.Dãy \[\left( {{u_n}} \right)\]là dãy giảm tới 1 khi \[n \to + \infty \]
B.Dãy \[\left( {{u_n}} \right)\]là dãy tăng tới 1 khi \[n \to + \infty \]
C.Không tồn tại giới hạn của dãy \[\left( {{u_n}} \right)\]
D.Cả 3 đáp án trên đều sai
Cho các số thực a, b thỏa \[\left| a \right| < 1,\;\;\left| b \right| < 1\]. Tìm giới hạn \[I = lim\frac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}\].
A.\[ + \infty \]
B. \[\frac{{1 - a}}{{1 - b}}\]
C. \[\frac{{1 - b}}{{1 - a}}\]
D. 1
Cho dãy số \[\left( {{u_n}} \right)\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_{n + 1}} = \sqrt {{u_n}({u_n} + 1)({u_n} + 2)({u_n} + 3) + 1} }\end{array}} \right.\left( {n \ge 1} \right)\) Đặt \[{v_n} = \sum\limits_{i = 1}^n {\frac{1}{{{u_i} + 2}}} \]. Tính \[lim\,{v_n}\]bằng?
A.\[ + \infty .\]
B. 0
C. \(\frac{1}{2}\)
D. 1
Giá trị của \[B = {\rm{lim}}\frac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }}\] bằng:
A.\[ + \infty \]
B. \[ - \infty \]
C. 0
D. 1
\[\lim \left( {\frac{2}{n} + \frac{3}{{{n^2}}}} \right)\]bằng
A.1
B.0
C.\[ + \infty \]
D. \(\frac{1}{2}\)
Tính giới hạn \[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\].
A.\[\frac{1}{5}\]
B. \(\frac{1}{2}\)
C. 0
D. \[\frac{{ - 3}}{2}\]
\[\lim \frac{{n + 1}}{{2n - 3}}\]bằng
A.0
B.\[ - \infty \]
C. \(\frac{1}{2}\)
D. \[ - \frac{1}{3}\]
Cho tam giác đều ABC cạnh a. Tam giác \[{A_1}{B_1}{C_1}\] có đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \[{A_2}{B_2}{C_2}\] có các đỉnh là trung điểm các cạnh của tam giác \[{A_1}{B_1}{C_1}\],…, tam giác AnBnCnAnBnCn có các đỉnh là trung điểm các cạnh của tam giác \[{A_{n - 1}}{B_{n - 1}}{C_{n - 1}} \ldots .{\rm{ }}Goi\;P,{P_1},{P_2},...,{P_n},...\] là chu vi của các tam giác \[ABC,{A_1}{B_1}{C_1},{A_2}{B_2}{C_2},...,{A_n}{B_n}{C_n},...\] Tìm tổng \[P,{P_1},{P_2},...,{P_n},...\]
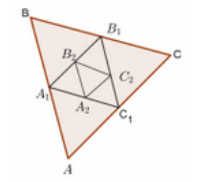
A.9a
B.6a
C.\[ + \infty \]
D.3a
Dãy \[\left( {{u_n}} \right)\]có giới hạn \[ - \infty \] ta viết là:
A.\[\mathop {\lim }\limits_{n \to - \infty } {u_n} = - \infty \]
B. \[\mathop {\lim }\limits_{n \to + \infty } {u_n} = - \infty \]
C. \[\mathop {\lim }\limits_{n \to - \infty } {u_n} = + \infty \]
D. \[\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \]
Cho cấp số nhân \[{u_n} = \frac{1}{{{2^n}}},\forall n \ge 1\]. Khi đó:
A.\[S = 1\]
B. \[S = \frac{1}{{{2^n}}}\]
C. \[S = 0\]
D. \[S = 2\]
![Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục (ảnh 1)](https://video.vietjack.com/upload2/images/1653298186/1653298389-image2.png)
Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục như thế, ta được hình vuông \[{A_3}{B_3}{C_3}{D_3}\] có diện tích \[{S_3}, \ldots \;\] Tính tổng \[{S_1} + {S_2} + \ldots \;\] bằng
A.\[\frac{{{a^2}\left( {{2^{100}} - 1} \right)}}{{{2^{100}}}}\]
B. \[2{a^2}\]
C. \[\frac{{{a^2}}}{{{2^{100}}}}\]
D. \[\frac{{{a^2}\left( {{2^{99}} - 1} \right)}}{{{2^{98}}}}\]