Giải SBT Toán 11 (Cánh Diều) Bài 2: Các phép biến đổi lượng giác

Cho hai góc a và b với tan a = $\frac{1}{7}$  và tanb = $\frac{3}{4}.$  Khi đó, tan(a + b) bằng:

A. 1.

B. $-\frac{17}{31}$ .

C. $\frac{17}{31}$ .

D. – 1.

Nếu $\sin \alpha =\frac{1}{\sqrt{3}}$  với $0<\alpha <\frac{\pi }{2}$  thì giá trị của $\cos \left(\alpha +\frac{\pi }{3}\right)$  bằng:

A. $\frac{\sqrt{6}}{6}-\frac{1}{2}$ .

B. $\sqrt{6}-3$ .

C. $\frac{\sqrt{6}}{6}-3$ .

D. $\sqrt{6}-\frac{1}{2}$.

Nếu $\sin \alpha =\frac{2}{3}$  thì giá trị của biểu thức $P=\left(1-3\cos 2\alpha \right)\left(2+3\cos 2\alpha \right)$  bằng:

A. $\frac{11}{9}$ .

B. $\frac{12}{9}$ .

C. $\frac{13}{9}$ .

D. $\frac{14}{9}$ .

Chọn đẳng thức đúng trong các đẳng thức sau:

A. ${\sin }^{4}x+{\cos }^{4}x=\frac{3-\cos 4x}{4}$ .

B. ${\sin }^{4}x+{\cos }^{4}x=\frac{3+\cos 4x}{4}$ .

C. ${\sin }^{4}x+{\cos }^{4}x=\frac{3+\cos 4x}{2}$ .

D. ${\sin }^{4}x+{\cos }^{4}x=\frac{3-\cos 4x}{2}$ .

Rút gọn biểu thức cos(120° – x) + cos(120° + x) – cos x ta được kết quả là:

A. – 2cos x.

B. – cos x.

C. 0.

D. sin x – cos x.

Nếu $\cos a=\frac{3}{4}$  thì giá trị của $\cos \frac{a}{2}\cos \frac{a}{2}$  bằng:

A. $\frac{23}{16}$ .

B. $\frac{7}{8}$ .

C. $\frac{7}{16}$ .

D. $\frac{23}{8}$ .

Nếu $\cos a=\frac{\sqrt{5}}{3}$  thì giá trị của biểu thức $A=4\sin \left(a+\frac{\pi }{3}\right)\sin \left(a-\frac{\pi }{3}\right)$  bằng:

A. $-\frac{11}{9}$ .

B. $\frac{11}{9}$ .

C. $-\frac{1}{9}$ .

D. $\frac{1}{9}$ .

Nếu $\cos a=\frac{1}{3},\sin b=\frac{-2}{3}$  thì giá trị cos(a + b) cos(a − b) bằng:

A. $-\frac{2}{3}$ .

B. $\frac{1}{3}$ .

C. $\frac{2}{3}$ .

D. $-\frac{1}{3}$ .

Giá trị của biểu thức $P=\frac{\sin \frac{\pi }{9}+\sin \frac{5\pi }{9}}{\cos \frac{\pi }{9}+\cos \frac{5\pi }{9}}$  bằng:

A. $\frac{1}{\sqrt{3}}$ .

B. $-\frac{1}{\sqrt{3}}$ .

C. $\sqrt{3}$ .

D. $-\sqrt{3}$ .                                             

Rút gọn biểu thức $A=\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$  ta được kết quả là:

A. tan x. 

B. tan 3x.

C. tan 2x.

D. tan x + tan 2x + tan 3x.

Cho $\sin a=\frac{2}{3}$  với $\frac{\pi }{2}<a<\pi$ . Tính:

a) cos a, tan a;

b) $\sin \left(a+\frac{\pi }{4}\right),\cos \left(a-\frac{5\pi }{6}\right),\tan \left(a+\frac{2\pi }{3}\right)$ ;

c) sin 2a, cos 2a.

Cho cos a = 0,2 với π < a < 2π. Tính $\sin \frac{a}{2}$ , $\cos \frac{a}{2}$ , $\tan \frac{a}{2}$ .

Cho cos(a + 2b) = 2cos a. Chứng minh rằng: tan(a + b) tan b = $\frac{-1}{3}$ .  

Cho tam giác ABC, chứng minh rằng:

a) tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);

b) $\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}=1$ .

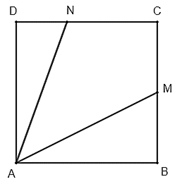
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = $\frac{1}{2}$BC, DN = $\frac{1}{3}$DC (Hình 4).

a) Tính $\tan \left(\widehat{BAM}+\widehat{DAN}\right)$ .

b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?

Hình 4