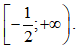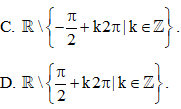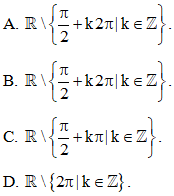Giải SBT Toán 11 (Cánh Diều) Bài 3: Hàm số lượng giác và đồ thị

Tập xác định của hàm số $y=\sqrt{1+\cos 2x}$  là:

A. ∅.

B. ℝ.

C. [– 1; + ∞).

D. 

Tập xác định của hàm số $y=\sqrt{\frac{1-\cos x}{1+\sin x}}$  là:

A. ℝ.

B. ∅.

Tập xác định của hàm số $y=\frac{1-\sin x}{\cos x}$  là:

Tập xác định của hàm số $y=\tan x+\frac{1}{1+{\cot }^{2}x}$  là:

Hàm số nào sau đây là hàm số lẻ?

A. y = – 2cos x.

B. y = – 2sin x.

C. y = tan x – cos x.

D. y = – 2 sin x + 2.  

Hàm số nào sau đây là hàm số chẵn?

A. y = cos x + 5.

B. y = tan x + cot x.

C. y = sin(– x).

D. y = sin x – cos x.

Hàm số y = cos x nghịch biến trên khoảng:

A. (0; π).

B. (π; 2π).

C. $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ .

D. (– π; 0).

Hàm số nào trong các hàm số sau đồng biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$ ?

A. y = sin x.

B. y = cos x.

C. y = tan x.

D. y = cot x.  

Hàm số y = sin x đồng biến trên khoảng:

A. $\left(\frac{9\pi }{2};\frac{11\pi }{2}\right)$ .

B. $\left(\frac{11\pi }{2};\frac{13\pi }{2}\right)$ .

C. (10π; 11π).

D. (9π; 10π).

Số giá trị α ∈ [− π; 2π] sao cho $\cos \alpha =\frac{1}{3}$  là:

A. 1.

B. 2.

C. 3.

D. 4.

Tìm tập xác định của các hàm số:

a) $y=\sqrt{1+\sin 3x}$ ;

b) $y=\frac{\sin 2x}{\sqrt{1-\cos x}}$ ;

c) $y=\frac{\sqrt{1+\cos 2x}}{\sin x}$ .

d) $y=\frac{1}{\sin x+\cos x}$ ;

e) $y=\frac{1}{1+\sin x\cos x}$ ;

g) $y=\sqrt{\cos x-1}$ .

Xét tính chẵn, lẻ của các hàm số:

a) y = sin 2x;

b) y = |sin x|;

c) y = tan² x;

d) $y=\sqrt{1-\cos x}$ ;

e) y = tan x + cot x;

g) y = sin x . cos 3x.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

a) y = 3sin x + 5; 

b) $y=\sqrt{1+\cos 2x}+3$ ;

c) y = 4 – 2sin x cos x;

d) $y=\frac{1}{4-\sin x}$ .  

Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

a) y = sin x trên khoảng $\left(-\frac{19\pi }{2};-\frac{17\pi }{2}\right),\left(-\frac{13\pi }{2};-\frac{11\pi }{2}\right)$ ;

b) y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

Từ đồ thị hàm số y = cos x, cho biết:

a) Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

b) Có bao nhiêu giá trị của x trên khoảng $\left(-\frac{9\pi }{2};-\frac{3\pi }{2}\right)$  để cos x = 0.

Từ đồ thị hàm số y = sin x, tìm:

a) Các giá trị của x để sin x = $\frac{1}{2}$ ;

b) Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương.

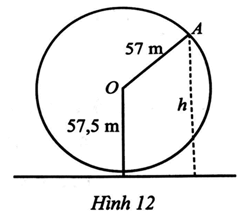
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

$h\left(t\right)=57\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)+\mathrm{57,5}$

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

a) Tính chu kì của hàm số h(t)?

b) Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

c) Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?