Giải SBT Toán 11 (Kết nối tri thức) Bài 14: Phép chiếu song song

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho $MB=2MC.$

a) Xác định hình chiếu M’ của M qua phép chiếu song song lên mặt phẳng (A’B’C’) theo phương AA’.

b) Chứng minh rằng $M^{\prime }{B}^{\prime }=2M^{\prime }{C}^{\prime }$

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD. Gọi O’ là hình chiếu của O qua phép chiếu song song lên mặt phẳng (A’B’C’D’) theo phương AA’. Chứng minh rằng O’ là giao điểm của A’C’ và B’D’.

Cho hình chóp S.ABCD có đáy ABCD không là hình thang.

a) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Xác định hình chiếu của điểm A qua phép chiếu song song lên mặt phẳng (SCD) theo phương SB.

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.

a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.

b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.

Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình vuông.

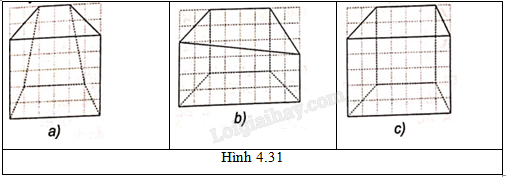
Trong các hình sau, hình nào là hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang?

Ba chiếc gậy được đặt dựa vào tường và đôi một song song với nhau (H.4.32). Giải thích vì sao nếu ba đầu gậy trên tường thẳng hàng thì ba đầu gậy trên sàn cũng thẳng hàng.