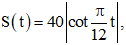Giải SBT Toán 11 (Kết nối tri thức) Bài 3: Hàm số lượng giác

Tìm tập xác định của các hàm số sau:

a) y = cot 3x;

b) $y=\sqrt{1-\cos 4x}$ ;

c) $y=\frac{\cos 2x}{{\sin }^{2}x-{\cos }^{2}x}$ ;

d) $y=\sqrt{\frac{1+\cos 2x}{1-\sin 2x}}$ .

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) y = 2 + 3|cosx|;

b) y = $2\sqrt{\sin x}$  + 1;

c) y = 3 cos² x + 4 cos2x;

d) y = sin x + cos x.

Xét tính chẵn lẻ của các hàm số sau:

a) $y=\frac{\cos 2x}{x^3}$ ;

b) y = x – sin 3x;

c) $y=\sqrt{1+\cos x}$ ;

d) $y=1+\cos x\sin \left(\frac{3\pi }{2}-2x\right)$ .

Xét tính tuần hoàn của các hàm số sau:

a) y = A sin(ωx + φ) với A > 0;

b) y = A tan(ωx + φ) với A > 0;

c) y = 3 sin 2x + 3cos 2x; 

d) $y=3\sin \left(2x+\frac{\pi }{6}\right)+3\sin \left(2x-\frac{\pi }{3}\right)$ .

Với giá trị nào của x, mỗi đẳng thức sau đúng?

a) tan x cot x = 1;

b) 1 + tan² x = $\frac{1}{{\cos }^{2}x}$ ;

c) 1 + cot² x = $\frac{1}{{\sin }^{2}x}$ ;

d) tan x + cot x = $\frac{2}{\sin 2x}$ .

Từ đồ thị hàm số y = cos x, hãy vẽ các đồ thị hàm số sau:

a) y = – cos x;

b) y = |cos x|;

c) y = cos x + 1;

d) $y=\cos \left(x+\frac{\pi }{2}\right)$ .

Từ đồ thị hàm số y = sin x, hãy xác định các giá trị của x trên đoạn   sao cho:

a) sin x = 0;                                       b) sin x > 0. 

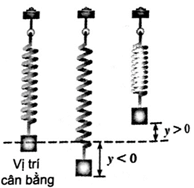
Một con lắc lò xo dao động điều hoà quanh vị trí cân bằng theo phương trình y = 25 sin 4πt ở đó y được tính bằng centimét còn thời gian t được tính bằng giây.

a) Tìm chu kì dao động của con lắc lò xo.

b) Tìm tần số dao động của con lắc, tức là số lần dao động trong một giây.

c) Tìm khoảng cách giữa điểm cao nhất và thấp nhất của con lắc.

Hằng ngày, Mặt Trời chiếu sáng, bóng của một toà chung cư cao 40 m in trên mặt đất, độ dài bóng của toà nhà này được tính bằng công thức

ở đó S được tính bằng mét, còn t là số giờ tính từ 6 giờ sáng.

a) Tìm độ dài bóng của toà nhà tại các thời điểm 8 giờ sáng, 12 giờ trưa, 2 giờ chiều và 5 giờ 45 phút chiều.

b) Tại thời điểm nào thì độ dài bóng của toà nhà bằng chiều cao toà nhà?

c) Bóng toà nhà sẽ như thế nào khi thời gian tiến dần đến 6 giờ tối?