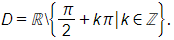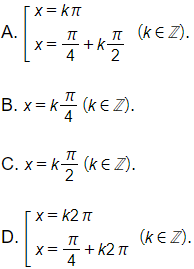Giải SBT Toán 11 (Kết nối tri thức) Bài tập cuối chương 1

Đổi số đo góc α = 105° sang rađian ta được

A. $\alpha =\frac{5\pi }{8}$.

B. $\alpha =\frac{\pi }{8}$.

C. $\alpha =\frac{7\pi }{12}$.

D. $\alpha =\frac{9\pi }{12}$.

Cho góc lượng giác (Ou, Ov) có số đo α mà $\widehat{uOv}$ là góc tù. Mệnh đề nào sau đây đúng?

A. Có số nguyên k để $\frac{\pi }{2}+k2\pi <\alpha <\frac{3\pi }{2}+k2\pi$.

B. $-\pi <\alpha <-\frac{\pi }{2}$.

C. $-\frac{\pi }{2}<\alpha \le \frac{3\pi }{2}$.

D. $\frac{\pi }{2}<\alpha <\pi$.

Giá trị $\cot \frac{89\pi }{6}$ bằng

A. $-\frac{\sqrt{3}}{3}$.

B. $\sqrt{3}$.

C. $-\sqrt{3}$.

D. $\frac{\sqrt{3}}{3}$.

Cho $\frac{\pi }{2}<\alpha <\pi$. Mệnh đề nào sau đây đúng?

A. sin α < 0; cos α > 0.

B. sin α > 0; cos α > 0.

C. sin α < 0; cos α < 0.

D. sin α > 0; cos α < 0. 

Trong các đẳng thức sau, đẳng thức nào sai?

A. $\sin \left(\frac{\pi }{2}-x\right)=\cos x$.

B. $\sin \left(\frac{\pi }{2}+x\right)=\cos x$.

C. $\tan \left(\frac{\pi }{2}-x\right)=\cot x$.

D. $\tan \left(\frac{\pi }{2}+x\right)=\cot x$.

Trong các đẳng thức sau, đẳng thức nào đúng?

A. sin(180° – a) = – cos a.

B. sin(180° – a) = – sin a.

C. sin(180° – a) = sin a.

D. sin(180° – a) = cos a.

Biết sin x = $\frac{1}{2}$. Giá trị của cos² x bằng

A. ${\cos }^{2}x=\frac{1}{2}$.

B. ${\cos }^{2}x=\frac{\sqrt{3}}{2}$.

C. ${\cos }^{2}x=\frac{1}{4}$.

D. ${\cos }^{2}x=\frac{3}{4}$.

Biết cot x = $\frac{1}{2}$. Giá trị của biểu thức $\frac{4\sin x+5\cos x}{2\sin x-3\cos x}$ bằng

A. $\frac{1}{17}$.

B. $\frac{5}{9}$.

C. 13.

D. $\frac{2}{9}$.

Trong các đẳng thức sau, đẳng thức nào sai?

A. $\cos u+\cos v=2\cos \frac{u+v}{2}\cos \frac{u-v}{2}$.

B. $\cos u-\cos v=2\sin \frac{u+v}{2}\sin \frac{u-v}{2}$.

C. $\sin u+\sin v=2\sin \frac{u+v}{2}\cos \frac{u-v}{2}$.

D. $\sin u-\sin v=2\cos \frac{u+v}{2}\sin \frac{u-v}{2}$.

Trong các đẳng thức sau, đẳng thức nào sai?

A. sin 2a = 2sin a cos a.

B. cos 2a = cos² a – sin² a.

C. cos 2a = 1 – 2sin² a.

D. tan 2a = $\frac{2\tan a}{1+{\tan }^{2}a}$.

Tập xác định của hàm số $y=\sqrt{1-\cos x}$ là

Khẳng định nào sau đây đúng?

A. Hàm số y = cos x nghịch biến trên khoảng (– π; 0) và đồng biến khoảng (0; π).

B. Hàm số y = cos x đồng biến trên các khoảng (– π; 0) và (0; π).

C. Hàm số y = cos x nghịch biến trên các khoảng (– π; 0) và (0; π).

D. Hàm số y = cos x đồng biến trên khoảng (– π; 0) và nghịch biến trên khoảng (0; π).

Khẳng định nào sau đây sai?

A. Tập xác định của hàm số y = tan x là 

B. Hàm số y = tan x đồng biến trên các khoảng $\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)$ với mọi k ∈ ℤ.

C. Tập giá trị của hàm số y = tan x là $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$.

D. Hàm số y = tan x là hàm số tuần hoàn với chu kì π.

Hàm số nào dưới đây có đồ thị nhận trục tung làm trục đối xứng?

A. y = cos x.

B. y = sin³ x .

C. y = sin x.

D. y = tan x.

Mệnh đề nào sau đây sai?

A. Hàm số y = sin x tuần hoàn với chu kì 2π.

B. Hàm số y = cos x tuần hoàn với chu kì 2π.

C. Hàm số y = tan x tuần hoàn với chu kì 2π.

D. Hàm số y = cot x tuần hoàn với chu kì π.

Mệnh đề nào sau đây sai?

A. Hàm số y = sin x cos 2x là hàm số tuần hoàn.

B. Hàm số y = sin x cos 2x là hàm số lẻ.

C. Hàm số y = x sin x là hàm số tuần hoàn.

D. Hàm số y = x sin x là hàm số chẵn.

Mệnh đề nào dưới đây đúng?

A. cos x = – 1 ⇔ x = π + k2π (k ∈ ℤ).

B. sin x = 0 ⇔ x = k2π (k ∈ ℤ).

C. tan x = 0 ⇔ x = k2π (k ∈ ℤ).

D. cos x = 0 ⇔ x = $\frac{\pi }{2}$ + k2π (k ∈ ℤ).

Số nghiệm của phương trình $2\cos x=\sqrt{3}$ trên đoạn  là

A. 1.

B. 4.

C. 3.

D. 2.

Tổng các nghiệm thuộc khoảng (0; 2π) của phương trình 3cos x – 1 = 0 bằng

A. S = 2π.

B. S = 0.

C. S = 4π.

D. S = 3π.

Giá trị của các hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi

Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng.

a) $\frac{23\pi }{4}$;                          b) $\frac{31\pi }{6}$;                          c) – 1 380°.

Kim phút và kim giờ của đồng hồ lớn nhà Bưu điện Thành phố Hà Nội theo thứ tự dài 1,75 m và 1,26 m. Hỏi trong 15 phút, mũi kim phút vạch nên cung tròn có độ dài bao nhiêu mét? Cũng câu hỏi đó cho mũi kim giờ.

Huyện lị Quản Bạ tỉnh Hà Giang và huyện lị Cái Nước tỉnh Cà Mau cùng nằm ở 105° kinh đông, nhưng Quản Bạ ở 23° vĩ bắc, Cái Nước ở vĩ độ 9° bắc. Hãy tính độ dài cung kinh tuyến nối hai huyện lị đó (khoảng cách theo đường chim bay), coi Trái Đất có bán kính 6 378 km.

Cho cos α = $\frac{3}{4}$, sin α > 0; sin β = $\frac{3}{5}$, $\beta \in \left(\frac{9\pi }{2};5\pi \right)$. Hãy tính cos 2α, sin 2α, cos 2β, sin 2β, cos (α + β), sin (α – β).

Rút gọn các biểu thức sau

a) $\frac{\sin \left(45°+\alpha \right)-\cos \left(45°+\alpha \right)}{\sin \left(45°+\alpha \right)+\cos \left(45°+\alpha \right)}$;

b) $\frac{\sin 2\alpha +\sin \alpha }{1+\cos 2\alpha +\cos \alpha }$;

c) $\frac{1+\cos \alpha -\sin \alpha }{1-\cos \alpha -\sin \alpha }$;

d) $\frac{\sin \alpha +\sin 3\alpha +\sin 5\alpha }{\cos \alpha +\cos 3\alpha +\cos 5\alpha }$.

Chứng minh các biểu thức sau không phụ thuộc vào x:

a) $A=\sin \left(\frac{\pi }{4}+x\right)-\cos \left(\frac{\pi }{4}-x\right)$;

b) $B=\cos \left(\frac{\pi }{6}-x\right)-\sin \left(\frac{\pi }{3}+x\right)$;

c) $C={\sin }^{2}x+\cos \left(\frac{\pi }{3}-x\right)\cos \left(\frac{\pi }{3}+x\right)$;

d) $D=\frac{1-\cos 2x+\sin 2x}{1+\cos 2x+\sin 2x}.\cot x$.

Hai sóng âm có phương trình lần lượt là

f1(t) = C sin ωt và f2(t) = C sin(ωt + α).

Hai sóng này giao thoa với nhau tạo ra một âm kết hợp có phương trình

f(t) =  f1(t) + f2(t) = C sin ωt + C sin(ωt + α).

a) Sử dụng công thức cộng chỉ ra rằng hàm f(t) có thể viết được dưới dạng f(t) = A sin ωt + B cos ωt, ở đó A, B là hai hằng số phụ thuộc vào α.

b) Khi C = 10 và $\alpha =\frac{\pi }{3}$, hãy tìm biên độ và pha ban đầu của sóng âm kết hợp, tức là tìm hai hằng số k và φ sao cho f(t) = k sin(ωt + φ).

Tìm tập xác định của các hàm số sau:

a) $y=\cos \frac{2x}{x-1}$;

b) $y=\frac{1}{\cos x-\cos 3x}$;

c) $y=\frac{1}{\cos x+\sin 2x}$;

d) y = tan x + cot x.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của p

a) y = sin x – cos x;

b) y = sin x + sin$\left(\frac{\pi }{3}-x\right)$;

c) y = sin⁴ x + cos⁴ x;

d) y = cos 2x + 2cos x – 1.

Xét tính chẵn lẻ của các hàm số sau:

a) y = sin³ x – cot x;

b) $y=\frac{\cos x+{\tan }^{2}x}{\cos x}$;

c) y = sin 2x + cos x;

d) $y=2\cos \left(\frac{3\pi }{4}+x\right)\sin \left(\frac{\pi }{4}-x\right)$.

Xét tính tuần hoàn của các hàm số sau:

a) y = sin$\frac{x}{2}$ + cos 3x;

b) y = cos 5x + tan$\frac{x}{3}$.

Giải các phương trình sau:

a) $\sin 3x=-\frac{\sqrt{3}}{2}$;

b) $\tan \left(\frac{x}{3}+10°\right)=-\frac{1}{\sqrt{3}}$;

c) sin 3x – cos 5x = 0;

d) tan 3x tan x = 1.

Giải các phương trình sau:

a) sin 5x + cos 5x = – 1;

b) cos 3x – cos 5x = sin x;

c) 2 cos² x + cos 2x = 2;

d) sin⁴ x + cos⁴ x = $\frac{1}{2}$sin² 2x.

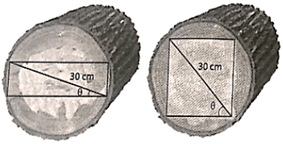
Một thanh xà gồ hình hộp chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30 cm.

a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức

S(θ) = 450 sin 2θ (cm²),

ở đó góc θ được chỉ ra trong hình vẽ dưới đây.

b) Tìm góc θ để diện tích mặt cắt của thanh xà gồ là lớn nhất.

Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu gọi là huyết áp tâm thu và tâm trương, tương ứng. Chỉ số huyết áp của chúng ta được viết là tâm thu/tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử một người nào đó có nhịp tim là 70 lần trên phút và huyết áp của người đó được mô hình hóa bởi hàm số

$P\left(t\right)=100+20\sin \left(\frac{7\pi }{3}t\right)$

ở đó P(t) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian t tính theo giây.

a) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 100 mmHg.

b) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 120 mmHg.