Giải SBT Toán 11 (Kết nối tri thức) Bài tập cuối chương 7

Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b song song với mặt phẳng (P). Góc giữa hai đường thẳng a và b bằng

A. 30°.

B. 90°.

C. 60°.

D. 0°.

Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b vuông góc với đường thẳng a. Phát biểu nào sau đây là đúng?

A. Đường thẳng b cắt mặt phẳng (P).

B. Đường thẳng b song song với mặt phẳng (P).

C. Đường thẳng b nằm trên mặt phẳng (P).

D. Đường thẳng b nằm trên mặt phẳng (P) hoặc song song với mặt phẳng (P).

Cho tứ diện đều ABCD, góc giữa hai đường thẳng AB và CD bằng

A. 30°.

B. 45°.

C. 60°.

D. 90°.

Cho tứ diện đều ABCD có cạnh bằng a, côsin của góc giữa đường thẳng AB và mặt phẳng (BCD) bằng

A. $\frac{1}{3}$ .

B. $\frac{\sqrt{3}}{3}$ .

C. $\frac{\sqrt{3}}{2}$ .

D. $\frac{1}{2}$ .

Cho tứ diện đều ABCD có cạnh bằng a, côsin của góc giữa hai mặt phẳng (ACD) và (BCD) bằng

A. $\frac{2}{3}$ .

B. $\frac{\sqrt{3}}{2}$ .

C. $\frac{\sqrt{3}}{3}$ .

D. $\frac{1}{3}$ .

Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách từ O đến mặt phẳng (SBC) bằng

A. $\frac{a\sqrt{6}}{6}$ .

B. $\frac{a\sqrt{3}}{3}$ .

C. $\frac{a\sqrt{3}}{2}$ .

D. $\frac{a\sqrt{6}}{3}$ .

Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách giữa hai đường thẳng AB và SD bằng

A. $\frac{a\sqrt{3}}{3}$ .

B. $\frac{a\sqrt{3}}{2}$ .

C. $\frac{a\sqrt{6}}{3}$ .

D. $\frac{a\sqrt{6}}{2}$ .

Cho lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ điểm A đến đường thẳng BB' bằng

A. $\frac{a\sqrt{7}}{2}$ .

B. $\frac{a\sqrt{14}}{4}$ .

C. $\frac{a\sqrt{7}}{4}$ .

D. $\frac{a\sqrt{14}}{2}$ .

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABC'D' bằng

A. $\frac{a^3}{3}$ .

B. $\frac{a^3}{2}$ .

C. $\frac{a^3}{6}$ .

D. $\frac{2a^3}{3}$ .

Cho hình hộp ABCD.A'B'C'D', gọi M là trung điểm của AA'. Tỉ số của thể tích khối chóp M.ABCD và khối hộp ABCD.A'B'C'D' bằng

A. $\frac{1}{3}$ .

B. $\frac{1}{2}$ .

C. $\frac{1}{6}$ .

D. $\frac{2}{3}$ .

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và SC = a$\sqrt{2}$ . Gọi H là trung điểm của cạnh AB.

a) Chứng minh rằng SH $\perp$ (ABCD).

b) Tính theo a thể tích khối chóp S.ABCD.

c) Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBD).

Cho hình chóp S.ABCD có SA $\perp$ (ABCD), biết ABCD là hình vuông cạnh bằng a và SA = a$\sqrt{2}$ .

a) Chứng minh rằng (SAC) $\perp$ (SBD) và (SAD) $\perp$ (SCD).

b) Gọi BE, DF là hai đường cao của tam giác SBD. Chứng minh rằng (ACF) $\perp$ (SBC) và (AEF) $\perp$ (SAC).

c) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.

Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA = $\frac{a\sqrt{5}}{2}$ . Gọi SM, SN lần lượt là đường cao của tam giác SAD và tam giác SBC.

a) Chứng minh rằng (SMN) $\perp$ (ABCD).

b) Tính số đo của góc nhị diện [S, AD, B].

c) Tính theo a thể tích khối chóp S.ABCD.

Cho hình lăng trụ đứng ABC.A'B'C' có $\widehat{BAC}=60°$ , AB = 2a, AC = 3a và số đo của góc nhị diện [A', BC, A] bằng 45°.

a) Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC).

b) Tính theo a thể tích khối lăng trụ ABC.A'B'C'.

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD.

a) Tính theo a thể tích khối chóp cụt AMN.A'B'D'.

b) Tính theo a khoảng cách giữa hai đường thẳng MN và A'B.

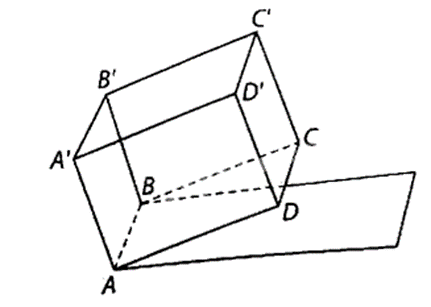
Một bể chứa nước hình hộp chữ nhật ABCD.A'B'C'D' được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc 10°, AB = 1 m, AD = 1,5 m, AA' = 1 m. Đáy bể là hình chữ nhật ABCD. Các điểm A, B cùng ở độ cao 5 m (so với mặt đất), các điểm C, D ở độ cao lớn hơn so với độ cao của các điểm A, B. Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng (ABB'A') và mặt đáy của bể là 80 cm. Tính thể tích của phần nước trong bể.