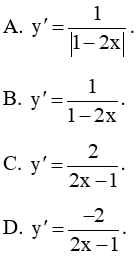Giải SBT Toán 11 (Kết nối tri thức) Bài tập cuối chương 9

Cho f(x) = cos²$\left(2x+\frac{\pi }{12}\right)$. Đạo hàm f'(0) bằng

A. 1.

B. −1.

C. 2cos$\frac{\pi }{12}$.

D. -2cos$\frac{\pi }{12}$.

Cho f(x) = -$\frac{1}{3}$x³+x²+3x - 1. Đạo hàm f'(x) > 0 khi

A. x < −1.

B. x > 3.

C. −1 < x < 3.

D. x > −1.

Đạo hàm của hàm số y = ln|1 – 2x| là

Đạo hàm của hàm số $y={\left(\frac{2x+1}{x-1}\right)}^3$ là

A. $3{\left(\frac{2x+1}{x-1}\right)}^2$ .

B. $-9\frac{{\left(2x+1\right)}^2}{{\left(x-1\right)}^5}$ .

C. $-9\frac{{\left(2x+1\right)}^2}{{\left(x-1\right)}^4}$ .

D. $9\frac{{\left(2x+1\right)}^2}{{\left(x-1\right)}^4}$ .

Đạo hàm của hàm số $y=\sqrt{1+2{\sin }^{2}x}$ là

A. $y^{\text{'}}=\frac{\sin 2x}{\sqrt{1+2{\sin }^{2}x}}$ .

B. $y^{\text{'}}=\frac{\sin 2x}{2\sqrt{1+2{\sin }^{2}x}}$ .

C. $y^{\text{'}}=\frac{2\sin 2x}{\sqrt{1+2{\sin }^{2}x}}$ .

D. $y^{\text{'}}=\frac{\sin x\cos x}{2\sqrt{1+2{\sin }^{2}x}}$ .

Đạo hàm của hàm số y = xsin²x là

A. y' = sin²x + 2xsinx.

B. y' = sin²x + xsin2x.

C. y' = sin²x + 2xcosx.

D. y' = sin²x + xcos2x.

Cho hàm số $f\left(x\right)=\sqrt{1+5g\left(x\right)}$ với g(0) = 3, g'(0) = −8. Đạo hàm f'(0) bằng

A. 10.

B. −8.

C. −5.

D. 5.

Cho f(x) = xsinx và g(x) = $\frac{\cos x}{x}$. Giá trị $\frac{f^{\text{'}}\left(1\right)}{g^{\text{'}}\left(1\right)}$ là

A. −1.

B. sin1 + cos1.

C. 1.

D. −sin1 − cos1.

Cho f(x) = x$e^{-\frac{x^2}{2}}$. Tập nghiệm của phương trình f'(x) = 0 là

A. {1}.

B. {−1}.

C. {0; 1}.

D. {−1; 1}.

Cho hai hàm số f(x) = 2x³ + 3x – 1 và g(x) = 3(x² + x) + 2. Tập nghiệm của bất phương trình f'(x) < g'(x) là

A. (−$\infty$; 0).

B. (1; +$\infty$).

C. (−$\infty$; 0) $\cup$ (1; +$\infty$).

D. (0; 1).

Cho S(r) là diện tích hình tròn bán kính r. Khẳng định nào sau đây đúng?

A. S'(r) là diện tích nửa hình tròn đó.

B. S'(r) là chu vi đường tròn đó.

C. S'(r) là chu vi nửa đường tròn đó.

D. S'(r) là hai lần chu vi đường tròn đó.

Tiếp tuyến của đồ thị hàm số y = x(x – 1)² + x² + 1 tại điểm A(−1; −2) có phương trình là

A. y = 6x + 4.

B. y = 6x − 4.

C. y = −2x − 4.

D. y = −2x + 4.

Tiếp tuyến của đồ thị hàm số $y=\frac{2}{3}{x}^3-4x^2+5x+3$ với hệ số góc nhỏ nhất có phương trình là

A. y = 3x − 25.

B. y = −3x + 25.

C. $y=-3x+\frac{25}{3}$.

D. $y=3x-\frac{25}{3}$.

Hệ số góc của tiếp tuyến của đồ thị hàm số $y=\frac{1-2x}{x+2}$ tại điểm có hoành độ x = −1 là

A. k = 5.

B. k = 2.

C. k = −2.

D. k = −5.

Tiếp tuyến của đồ thị hàm số y = −x³ + 6x² – 9x + 1 với hệ số góc lớn nhất có phương trình là

A. y = 3x – 5.

B. y = 3x – 7.

C. y = 3x + 5.

D. y = 3x + 7.

Cho f(x) = (x² – x)e^−x. Giá trị f'(0) là

A. 4.

B. −4.

C. 0.

D. −1.

Cho hàm số y = e^xcosx. Đẳng thức đúng là

A. y' – 2y' – 2y = 0.

B. y' – 2y' + 2y = 0.

C. y' + 2y' – 2y = 0.

D. y' + 2y' + 2y = 0.

Độ cao (tính bằng mét) của một vật rơi tự do sau t giây là h(t) = 400 – 4,9t². Giá trị tuyệt đối của vận tốc của vật khi nó chạm đất (làm tròn kết quả đến chữ số thập phân thứ nhất) là

A. 88,5 m/s.

B. 86,7 m/s.

C. 89,4 m/s.

D. 90 m/s.

Chuyển động của một vật có phương trình s = 5+ sin$\left(0,8\pi t+\frac{\pi }{6}\right)$, ở đó s tính bằng centimét và thời gian t tính bằng giây. Tại các thời điểm vận tốc bằng 0, giá trị tuyệt đối của gia tốc của vật gần với giá trị nào sau đây nhất?

A. 4,5 cm/s².

B. 5,5 cm/s².

C. 6,3 cm/s².

D. 7,1 cm/s².

Vị trí của một vật chuyển động (tính bằng mét) sau t giây được xác định bởi s = t⁴ – 4t³ – 20t² + 20t, t > 0. Gia tốc của vật tại thời điểm mà vận tốc v = 20 m/s là

A. 140 m/s².

B. 120 m/s².

C. 130 m/s².

D. 100 m/s².

Tính đạo hàm các hàm số sau:

a) $y={\left(x^2-\frac{2}{x}+4\sqrt{x}\right)}^3$

b) y = 2^x + log₃(1 – 2x);

c) $y=\frac{1-2x}{x^2+1}$;

d) y = sin2x + cos²3x.

Cho hàm số f(x) = x + $\sqrt{4+x^2}$.

a) Tìm tập xác định của hàm số đã cho.

b) Tính đạo hàm f'(x) và tìm tập xác định của f'(x).

c) Tìm x sao cho f'(x) = 0.

Cho hàm số f(x) = 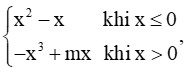 với m là tham số. Tìm m để hàm số có đạo hàm tại mọi x $\in$ ℝ.

Cho hàm số f(x) = x³ + ax² + 3x + 1 (a $\in$ ℝ là tham số). Tìm a để f'(x) > 0 với mọi x $\in$ ℝ.

Cho hàm số y = x³ – 3x² + 2x – 1 có đồ thị là đường cong (C). Tìm tọa độ điểm M thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại điểm M song song với đường thẳng có phương trình y = 2x – 1.

Viết phương trình tiếp tuyến của đồ thị hàm số y = (x² – 1)² – 3 tại các giao điểm của nó với đồ thị hàm số y = 10 – x².

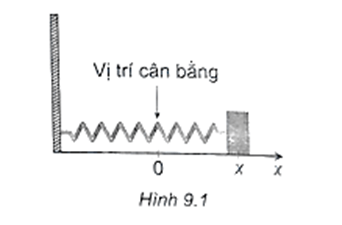
Một vật gắn trên lò xo chuyển động theo phương ngang trên một mặt phẳng nhẵn (H.9.1). Phương trình chuyển động của vật được cho bởi $x=8\sin \left(\sqrt{2}\pi t+\frac{\pi }{3}\right)$, với t tính bằng giây và x tính bằng centimét. Tìm vận tốc và gia tốc của vật tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất). Vật chuyển động theo hướng nào tại thời điểm đó?