Giải Toán 12 (Kết nối tri thức) Bài tập cuối chương 1 trang 42
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho hàm số có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?
A. Nếu với mọi x thuộc (a; b) thì hàm số đồng biến trên (a; b).
B. Nếu với mọi x thuộc (a; b) thì hàm số đồng biến trên (a; b).
C. Hàm số đồng biến trên (a; b) khi và chỉ khi với mọi x thuộc (a; b).
D. Hàm số đồng biến trên (a; b) khi và chỉ khi với mọi x thuộc (a; b).
Hàm số nào sau đây nghịch biến trên ?
A. ;
B. ;
C. ;
D. .
Hàm số nào dưới đây không có cực trị?
A. .
B. .
C. .
D. .
Giá trị cực tiểu của hàm số là
A. .
B. .
C. .
D. .
A. 0.
B. .
C. .
D. e.
Cho hàm số thỏa mãn: và . Khẳng định nào sau đây là đúng?
A. Đường thẳng là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng là tiệm cận ngang của đồ thị hàm số.
Tiệm cận xiên của đồ thị hàm số là
A. .
B. .
C. .
D. .
Cho hàm số xác định trên, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai?
A. Đường thẳng là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng là tiệm cận đứng của đồ thị hàm số đã cho.
Đồ thị trong Hình 1.37 là đồ thị của hàm số:
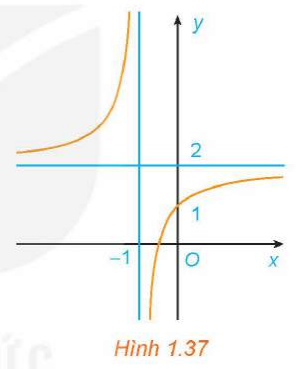
A. .
B. .
C. .
D. .
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
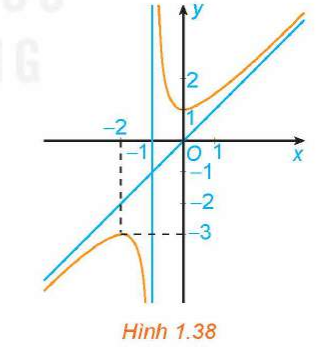
A. .
B. .
C. .
D. .
b) ;
c) ;
d) .
a) trên nửa khoảng ;
b) ;
a) ;
b) .
a) ;
b) ;
c) .
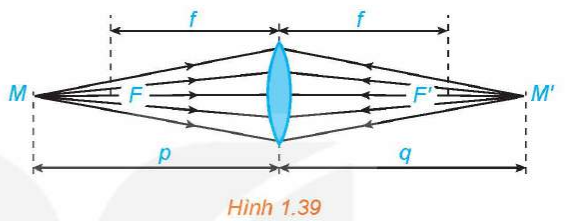
a) Viết công thức tính như một hàm số của biến .
b) Tính các giới hạn và giải thích ý nghĩa các kết quả này.
Lập bảng biến thiên của hàm số trên khoảng .
a) Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).
b) Xem N(t) là hàm số của biến số t xác định trên đoạn [0; 50]. Xét chiều biến thiên của hàm số N(t) trên đoạn [0; 50].
c) Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/ năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm?
↵