Hàm số lũy thừa
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Hàm số nào dưới đây KHÔNG là hàm số lũy thừa?
A.\[y = \frac{1}{{{x^4}}}\]
B. \[y = {x^{ - \sqrt 2 }}\]
C. \[y = {e^x}\]
D. \[y = {x^\pi }\]
Chọn kết luận đúng:
A.Hàm số \[y = {x^\alpha }\] có TXĐ \[D = R\;\] với mọi \[\alpha \in R\].
B.Hàm số \[y = {x^\alpha }\]có TXĐ \[D = R\;\] với mọi \[\alpha \in R\].
C.Hàm số \[y = {x^\alpha }\]có TXĐ \[D = R \setminus \left\{ 0 \right\}\] với mọi \[\alpha \in R\].
D.Hàm số \[y = {x^\alpha }\] có TXĐ \[D = \left( {0; + \infty } \right)\] với mọi \[\alpha \] không nguyên.
Chọn khẳng định đúng:
A.Với \[n \in {N^ * }\] thì \[\sqrt[n]{x} = {x^{\frac{1}{n}}}\] nếu x>0.
B.Với n \[n \in {N^ * }\]thì \[\sqrt[n]{x} = {x^{\frac{1}{n}}}\]nếu \[x \ge 0\].
C.Với \[n \in {N^ * }\] thì n \[\sqrt[n]{x} = {x^{\frac{1}{n}}}\]nếu x<0.
D.Với \[n \in {N^ * }\] thì \[\sqrt[n]{x} = {x^{\frac{1}{n}}}\] nếu \[x \ne 0\].
Công thức tính đạo hàm của hàm số \[y = {x^\alpha }\] là:
A.\[y' = \alpha {x^{\alpha - 1}}\]
B. \[y' = \left( {\alpha - 1} \right){x^{\alpha - 1}}\]
C. \[y' = \alpha {x^\alpha }\]
D. \[y' = \alpha {x^\alpha } - 1\]
Đẳng thức \[{\left( {\sqrt[n]{x}} \right)^\prime } = ({x^{\frac{1}{n}}})' = \frac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \frac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\] xảy ra khi:
A.x<0
B.x>0
C.\[x \ge 0\]
D.\[x \in R\]
Chọn kết luận đúng:
A.Hàm số \[y = {x^\alpha }\left( {\alpha \ne 0} \right)\] đồng biến trên \[\left( {0; + \infty } \right)\]nếu \[\alpha < 0\].
B.Hàm số \[y = {x^\alpha }\left( {\alpha \ne 0} \right)\] nghịch biến trên \[\left( {0; + \infty } \right)\] nếu \[\alpha < 0\].
C.Hàm số \[y = {x^\alpha }\left( {\alpha \ne 0} \right)\] đồng biến trên \[\left( {0; + \infty } \right)\] nếu \[\alpha \ne 0\].
D.Hàm số \[y = {x^\alpha }\left( {\alpha \ne 0} \right)\] nghịch biến trên \[\left( {0; + \infty } \right)\] nếu \[0 < \alpha < 1\].
Cho hàm số \[y = {x^\alpha }\]. Nếu \[\alpha = 1\;\] thì đồ thị hàm số là:
A.đường thẳng
B.đường tròn
C.đường elip
D.đường cong
Xét hàm số \[y = {x^\alpha }\] trên tập \[\left( {0; + \infty } \right)\;\]có đồ thị dưới đây, chọn kết luận đúng:
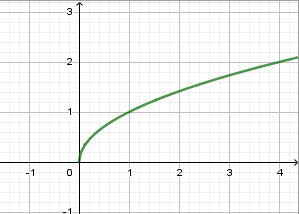
A.\[\alpha = 0\]
B. \[\alpha = 1\]
C. \[\alpha > 1\]
D. \[0 < \alpha < 1\]
</>
Cho hàm số \[y = {x^{e - 3}}\]. Trong các kết luận sau kết luận nào sai?
A.Đồ thị hàm số luôn đi qua điểm M(1;1)
B.Hàm số luôn đồng biến trên \[\left( {0; + \infty } \right)\;\]
C.Tập xác định của hàm số là \[D = \left( {0; + \infty } \right)\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;\;\]
D.Đồ thị hàm số nhận Ox,Oy làm hai tiệm cận
Tìm TXĐ của hàm số \[y = {\left( {{x^3} - 27} \right)^{\frac{\pi }{2}}}\]
A.\[D = R \setminus \left\{ 2 \right\}\]
B. \[D = R\]
C. \[D = \left[ {3; + \infty } \right)\]
D. \[D = \left( {3; + \infty } \right)\]
Tập xác định D của hàm số \[y = {\left( {{x^4} - 3{x^2} - 4} \right)^{ - 2}}\] là:
A.\[D = R \setminus \left\{ { \pm 2} \right\}\]
B. \[D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\]
C. \[D = \left( { - \infty ; - 1} \right) \cup \left( {4; + \infty } \right)\]
D. \[D = R\]
Rút gọn biểu thức \[P = {x^{\frac{1}{3}}}\sqrt[6]{x}\]với x > 0.
A.\[P = {x^2}\]
B. \[P = \sqrt x \]
C. \[P = {x^{\frac{1}{3}}}\]
D. \[P = {x^{\frac{1}{{18}}}}\]
Cho hàm số \[f\left( x \right) = {\left( {{x^{1 + \frac{1}{{2{{\log }_4}x}}}} + {8^{\frac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\frac{1}{2}}} - 1\] với \[0 < x \ne 1\]. Tính giá trị biểu thức \[P = f\left( {f\left( {2018} \right)} \right).\]
A.\[P = 2016\]
B. \[P = 1009\]
C. \[P = 2018\]
D. \[P = {2018^2}\]
Tính đạo hàm của hàm số \[y = {\left( {2{x^2} + x - 1} \right)^{\frac{2}{3}}}\].
A.\[y' = \frac{{2\left( {4x + 1} \right)}}{{3\sqrt[3]{{2{x^2} + x - 1}}}}\] với \[x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\]
B. \[y' = \frac{{2\left( {4x + 1} \right)}}{{3\sqrt[3]{{{{\left( {2{x^2} + x - 1} \right)}^2}}}}}\] với\[x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\]
C. \[y' = \frac{{2\left( {4x + 1} \right)}}{{3\sqrt[3]{{2{x^2} + x - 1}}}}\] với\[x \in R\]
D. \[y' = \frac{{3\left( {4x + 1} \right)}}{{2\sqrt[3]{{{{\left( {2{x^2} + x - 1} \right)}^2}}}}}\] với\[x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\]
Cho hàm số \[y = f\left( x \right) = {\left( {{x^2} + x - 2} \right)^{\frac{2}{3}}}\]. Chọn khẳng định sai:
A.\[f'\left( 0 \right) = - \frac{2}{{3\sqrt[3]{2}}}\]
B. \[f'\left( 2 \right) = \frac{{10}}{{3\sqrt[3]{4}}}\]
C. \[f'\left( { - 3} \right) = - \frac{{10}}{{3\sqrt[3]{4}}}\]
D. \[f'\left( 3 \right) = \frac{{14}}{{3\sqrt[3]{{10}}}}\]
Cho đồ thị của ba hàm số \[y = {x^a};y = {x^b};y = {x^c}\] trên khoảng \[\left( {0; + \infty } \right)\;\]trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
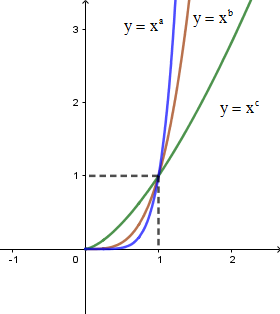
A.c<b<a<0
</b<a<0 >
B.0<c<b<a<1
</c<b<a<1
C.1<c<b<a
</c<b<a
D.0<a<b<c<1
</a<b<c<1
Cho hàm số \[y = {\left( {x + 2} \right)^{ - 2}}\]. Hệ thức giữa y và y″ không phụ thuộc vào x là:
A.\[y'' + 2y = 0\]
B. \[y'' - 6{y^2} = 0\]
C. \[2y'' - 3y = 0\]
D. \[{\left( {y''} \right)^2} - 4y = 0\]
Hàm số nào sau đây không có đường tiệm cận.
A.\[y = {x^{ - \frac{1}{2}}}\]
B. \[y = {x^{ - \frac{4}{3}}}\]
C. \[y = {x^{ - 2}}\]
d. \[y = {x^{\frac{1}{3}}}\]
Trên đồ thị (C) của hàm số \(y = {x^{\frac{\pi }{2}}}\) lấy điểm M0 có hoành độ x0=1. Tiếp tuyến của (C) tại điểm M0 có phương trình là:
A.\[y = \frac{\pi }{2}x + 1\]
B. \[y = \frac{\pi }{2}x - \frac{\pi }{2} + 1\]
C. \[y = \pi x - \pi + 1\]
D. \[y = - \frac{\pi }{2}x + \frac{\pi }{2} + 1\]
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
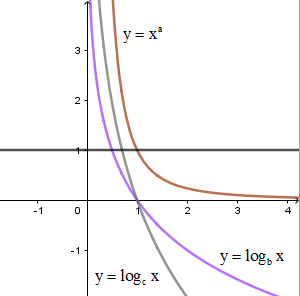
A.a<c<b
B.a<b<c
C.a>b>c
D.a>c>b
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
A.a<c<b
B.a<b<c
C.a>b>c
D.a>c>b